Путенихин П.В. Правила счета элементов бесконечного множества, ч.3
| [ Скачать с сервера (1.61 Mb) · Скачать удаленно (1,61 Mb) · Скриншот ] | 01.06.2021, 15:39 |
Часть 2 - URL: http://moianauka.ru/load/2-1-0-1509 Часть 3 - URL: http://moianauka.ru/load/2-1-0-1510 ЧАСТЬ 3 Аннотация Вскрыты ошибки Кантора и его последователей в логических рассуждениях о бесконечных множествах. Приведено доказательство счетности континуума, счетности всех действительных чисел. Показана ошибочность рассуждений в задаче об "Отеле Гильберта". Rules for counting elements of an infinite set. The mistakes of Cantor and his followers in logical reasoning about infinite sets are revealed. The proof of the countability of the continuum, the countability of all real numbers is given. The erroneousness of reasoning in the problem of "Hilbert's Hotel" is shown. Оглавление ЧАСТЬ 1 Связь математики и физики Равномощные множества чисел Количества натуральных чисел в группах О счетности континуума - точек на отрезке Задача об "Отеле Гильберта" ЧАСТЬ 2 Несостоявшаяся перепись Разрядность и количество чисел в массиве Счетность всех мыслимых видов чисел О равномощности отрезка и квадрата ЧАСТЬ 3 Стереографическая проекция Литература Стереографическая проекция В заключение отметим, что один из истоков или примеров отождествления бесконечностей разной мощности можно обнаружить в механизме стереографической проекции, также фактически отождествляющей точку и отрезок. Рассмотрим соотношение между размерами двух отрезков, которые затем сожмем в точки: 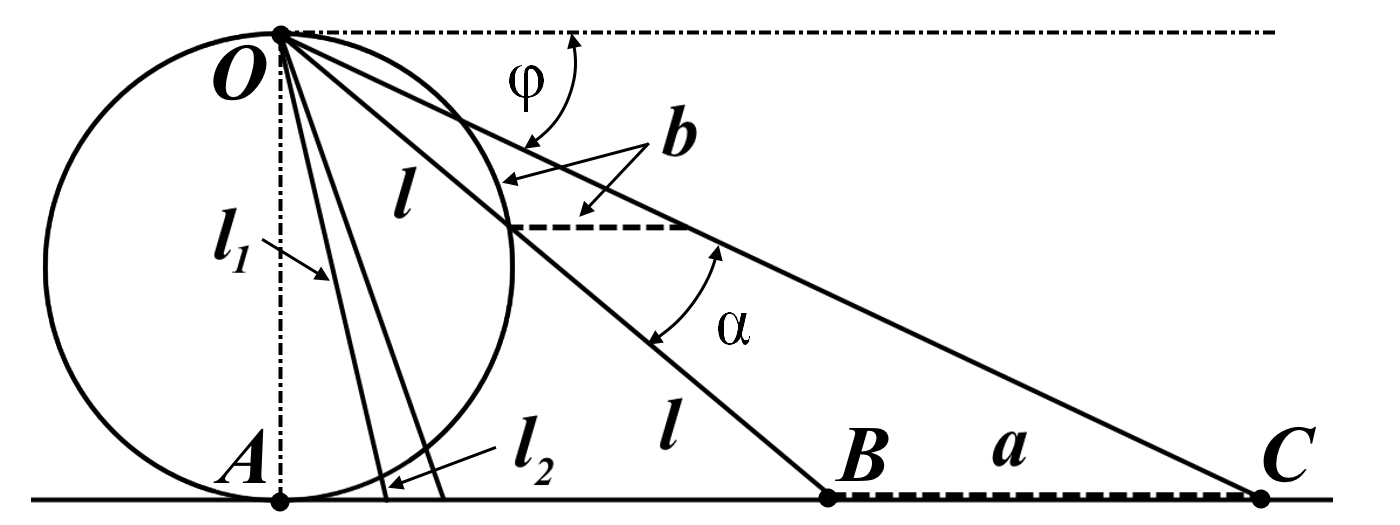 $IMAGE6$ - Скриншот Рис.3. Стереографическая проекция отождествляет отрезок и точку Мы не описываем сущность стереографической проекции, её описание можно найти в литературе. Каждая проекционная линия, прямая делится проецируемой точкой окружности между полюсом и проекционной плоскостью на две части, например, l1 и l2. Возьмем частный случай, когда отрезок делится пополам, то есть, l1 = l2 = l. Проведем ещё одну проекционную линию под углом ? к исходной линии. В этом случае на окружности образуется дуга, а на плоскости - отрезок. Проведем из проецируемой точки пересечения дополнительный отрезок между проекционными лучами параллельно плоскости из проецируемой точки. Обозначим полученный отрезок через b, а проекцию на плоскости - через a. Из подобия треугольников следует, что 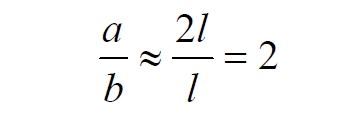 Здесь знак неточного равенства взят из предположения, что отрезок b приблизительно равен длине дуги. Это не точное равенство, но в средней части окружности отрезок и дуга отличаются друг от друга незначительно, в конечное число раз. Теперь найдем предел этого отношения, когда угол между двумя проецирующими прямыми стремится к нулю: 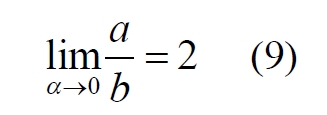 Это очевидный и аналитически достоверный предел. Но при этом возникает вопрос: что же означает это отношение 2? Две проекционные прямые слились в одну, и эта прямая пересекает и окружность и плоскость в одной точке каждую. Что же означает это соотношение для двух разных точек? Если считать, что точка - это то, что не имеет частей, то ответ становится совершенно туманным. Выходит, что точки не имеют частей, но в разном количестве. В любом случае для утверждения, что точка на окружности спроектировалась в единственную тождественную точку на плоскости, четких, бесспорных оснований уже нет. Однако это соотношение мы нашли для конкретного, среднего угла. А что если пару прямых, проектирующих лучей повернуть ближе к горизонтальному направлению? То есть, устремить к нулю не только угол между проецирующими прямыми, но и их средний угол к плоскости. В этом случае мы увидим, что отношение будет стремиться к бесконечности: 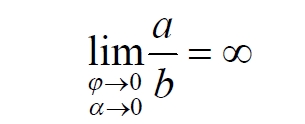 Вопрос о смысле этого отношения становится еще более острым. Если две точки - исходная, проецируемая и её проекция - отождествляются, тогда что означает это отношение? Изначально оно составлялось как отношение длины проецируемого отрезка и проекции, которые в дальнейшем уменьшением угла до нуля были преобразованы в точки. Хотя точка и не имеет частей, но величина соотношения определенно выглядит как количество проецируемых точек в проекции. Звучит весьма странно: проецирующий луч создаёт проекцию, имеющую явно не нулевые, не точечные размеры. Можно сколько угодно с этим не соглашаться, но как можно иначе рационально объяснить это соотношение? Обычно бесконечно малые величины в алгебре характеризуются параметром порядка малости. Если две величины имею отношение конечной величины, то они считаются величинами одного порядка малости. Если отношение стремится к бесконечности, то величины имеют разный порядок малости. С учетом этого следует предположить, что стереографическая проекция окружности на плоскость некорректна, а проекциями её точек фактически являются плоские фигуры, отрезки. Рассмотрим эту же ситуацию с другой точки зрения, не отождествляя дугу окружности и прямой отрезок. Для этого нам понадобится следующее интересное соотношение, теорема. Если к отрезку дуги провести по два луча из центра окружности (рис.4) и из любой точки окружности, кроме точек этой дуги, то угол между лучами в первом случае будет в два раза больше угла между лучами во втором случае. Приведем краткое доказательство этой теоремы. 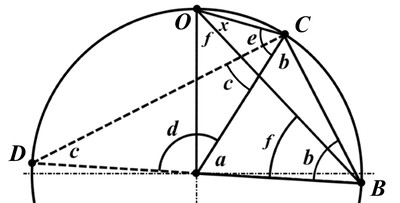 Рис.4. Теорема об углах на дуге окружности Итак, возьмем на окружности рис.4 некоторую произвольную дугу CB и проведем к ней две пары лучей - из центра и из полюса О. Проведем далее вспомогательный диаметр BD и линию CD. Обозначим одинаковыми буквами равные углы в равносторонних треугольниках у равных сторон. По условиям задачи нам задан некий центральный угол a. Докажем, что а = 2x. Из построений на рисунке видим: 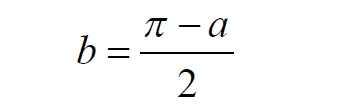 Угол при вершине штрихового треугольника: 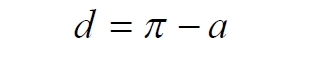 Углы при основании равностороннего треугольника. 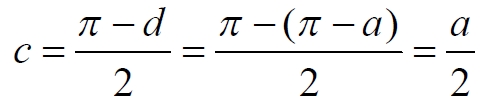 Углы при основании равностороннего треугольника с искомым углом: 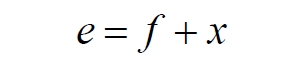 Составляем баланс углов в треугольнике с искомым углом x: 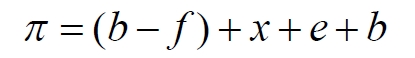 Подставляем условно известное значение угла f: 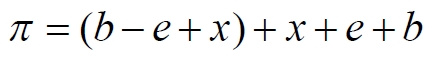 Раскрываем скобки 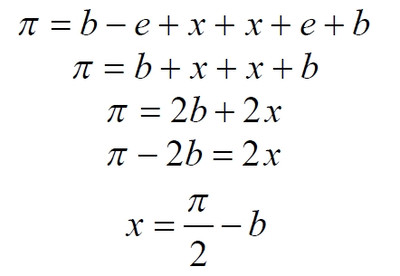 Подставляем значение заданного угла а 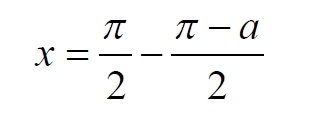 Упрощаем выражение 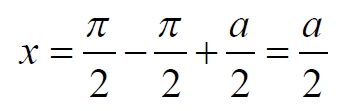 Что и требовалось доказать. Согласно этой теореме, на рис.3 длина дуги окружности в пределах угла α равна 2α R, поскольку угловая величина дуги равна 2α. Длину линии проекции a в основании проекционного угла найдем как разницу сторон двух прямоугольных треугольников: 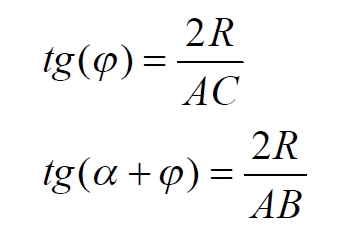 Отсюда находим величину а: 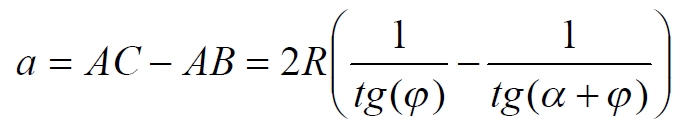 Как и выше, найдем отношение длины отсекаемой на окружности дуги к длине этого отрезка: 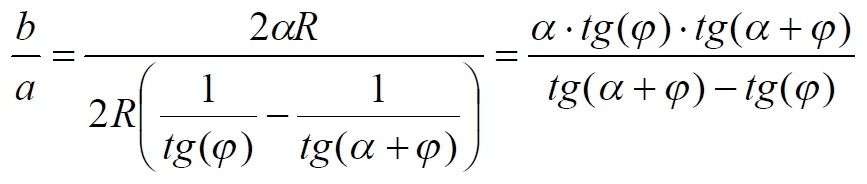 Найдем предел этой величины, когда каждый из углов стремится к нулю. В этом случае обе проекционные линии сблизятся до слияния, а их средняя линия будет стремиться к горизонтальному положению: 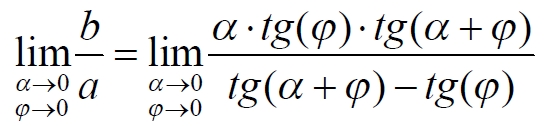 В общем случае мы получаем неопределенность, поскольку к нулю стремятся и числитель и знаменатель. Поэтому мы поступим следующим образом. Найдем эти пределы для нескольких конкретных значений среднего проекционного угла φ. В этом случае неопределенность не устраняется, но мы табличным методом построим соответствующие графики, которые визуально продемонстрируют наличие конечных пределов. Табличные значения сходятся удовлетворительно быстро, поэтому в пределах точности приложения Excel были получены следующие значения пределов для произвольно взятых значений угла φ:  Как видим, пределы существуют для любого значения проецирующей линии, угла проецирования. Поскольку вычисление предела функции неочевидно, приведём геометрический способ его вычисления для частного значения угла, рассмотренного на рис.3, значение которого определяется из геометрических соображений и равно 45о. Увеличим до бесконечности масштаб фрагмента рисунка в точке пересечения проецирующей прямой и окружности: 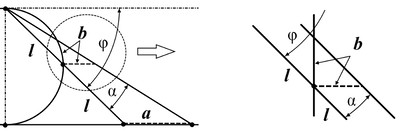 Рис.5. Увеличенный фрагмент рисунка 3 На рисунке угол φ =45о, а угол α → 0[/b]. Как видим на рисунке, фрагмент проецируемой окружности выглядит вертикальной прямой, а две проецирующие прямые - параллельны. Следовательно, отрезки b - на окружности и параллельный проецирующей плоскости оказываются перпендикулярными и образуют равносторонний прямоугольный треугольник. Отсюда и следует значение предела lim = 0,5 в третьей строке таблицы пределов и в выражении (9). Очевидно, что геометрическое вычисление предела несложно сделать и для других углов проецирующего луча. Напротив, определить это значение аналитически, вычислением предела выражения: 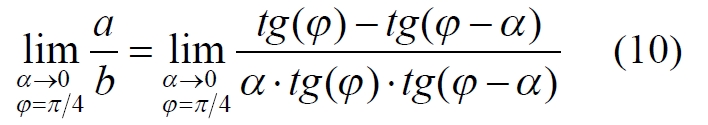 довольно сложно. Подставим значение угла φ 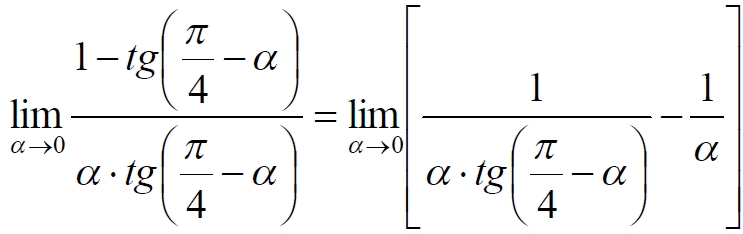 Как видим, под знаком предела находится разность двух бесконечно больших величин, причем это не просто равномощные бесконечности, они тождественны. Действительно, в пределе α → 0 мы имеем: 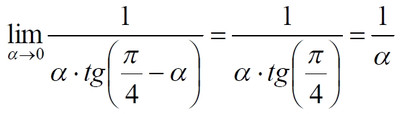 Что и можно записать как тождество 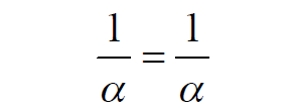 Это довольно интересное обстоятельство: две бесконечности равны, однако, тем не менее, дают разность 2. В общем-то, это свойство не уникально. Его легко показать на другом примере: n + 2 = n, если n → ∞. Здесь также две равные бесконечности, но при вычитании одной из другой мы получаем конечное число. Значение предела (10) нам известно, он равен 2, то есть при α → 0[/b] мы имеем 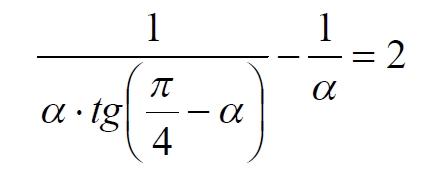 Получается, что тангенс в знаменателе, меньший единицы на бесконечно малую величину, вносит в значение бесконечно большой величины весьма существенный вклад, увеличивая её ровно на 2. Прямое вычисление выражения (10) в приложении Excel при уменьшении угла α до величины 10-9 дало устойчивое стремление значения предела к 2 с погрешностью 10-8. Дальнейшее уменьшение угла не имеет смысла ввиду ограниченной точности вычисления функций приложением. Таким образом, можно достаточно уверенно заявить, что стереографическое проецирование, преобразование фактически отождествляет точку и линию. И только единственная - вертикальная - проекция отождествляет точку на сфере с точкой на плоскости - это точка их касания. Верхняя точка, полюс проецируется фактически в линию бесконечной длины. Здесь мы рассматривали проецирование круга. Очевидно, что точка сферы проецируется не в отрезок, а в плоскую фигуру. В этом случае явно напрашивается предположение о форме самого проецирующего луча, который теперь уже формально может и даже обязан иметь некое сечение: круглое, квадратное, в форме звезды и так далее. Вместе с тем, вполне ожидаемо может возникнуть возражение: а почему, собственно, мы рассматривали две проецирующие линии? В традиционном варианте линия всегда одна, поэтому, казалось бы, проекцией каждой точки может быть только точка. Сразу же можно заметить, что это весомый довод в пользу формализма Кантора, который весьма схожим способом отождествил множество точек линии с множеством точек плоской фигуры - квадрата. Ответ достаточно простой. Рассмотренный способ показывает, что любые две смежные бесконечно близкие точки окружности (сферы) на проекционной плоскости позволяют поместить между ними некоторое количество, вплоть до бесконечности, таких же точек. Если рассматривать дискретное пространство, вплоть до планковских размеров, то появление на проекции дополнительных элементов практически неразрешимая проблема. Единичный проекционный луч просто делает эту проблему незаметной. С другой стороны, стремление к нулю угла между рассмотренными проецирующими лучами отождествляет их, превращает в одну линию, единый луч. И в этом случае возникает важный встречный вопрос: что же тогда означают вычисленные пределы? Какой математический, физический и даже философский смысл имеют эти величины? Ответ очевиден: это скрытное канторовское отождествление точки и линии, того, что не имеет частей, с тем, что может делиться на части. Литература 1. Бесконечность, Википедия, URL: <a href="https://ru.wikipedia.org/wiki/п"пЅяЃпЊпЎпҐпЅя‡пҐпЎяЃя‚яЊ">https://ru.wikipedia.org/wiki/Бесконечность</a> 2. Виленкин А., Мир многих миров: Физики в поисках параллельных вселенных Алекс Виленкин, пер. с англ. А. Сергеева. -- М.: ACT: Астрель : CORPUS, 2010. -- 303, [1] с. -- (ЭЛЕМЕНТЫ) 3. Виленкин Н.Я., В поисках бесконечности.-- М.: Наука, 1983. 160 с. 4. Горелик Г.Е., Почему пространство трехмерно? М.: Наука, 1982, 168 с. 5. Крейг У., Самое начало. Происхождение Вселенной и существование Бога, URL: <a href="http://www.otkrovenie.de/beta/xml/other/samoeNachalo.xml">http://www.otkrovenie.de/beta/xml/other/samoeNachalo.xml</a> 6. Линде А.Д., Инфляция, квантовая космология и антропный принцип. Перевод Карпова С., URL: https://arxiv.org/abs/hep-th/0211048 7. Новиков И. Д., Черные дыры и Вселенная. -- М.: Мол. гвардия, 1985. -- 190 с., ил.-- (Эврика). 8. Парадокс Гильберта, URL: <a href="http://pikabu.ru/story/paradoks_gilberta_1962200">http://pikabu.ru/story/paradoks_gilberta_1962200</a> , <a href="http://www.yaplakal.com/forum3/topic782267.html">http://www.yaplakal.com/forum3/topic782267.html</a> 9. Парадокс Гильберта, URL: <a href="http://traditio-ru.org/wiki/п¤п№яЂп№пЄпЎпЊяЃ_п"пЈп"яЊпЂпЅяЂя‚a">http://traditio-ru.org/wiki/Парадокс_Гильбертa</a> 10. Парадокс Гильберта, Википедия, URL: <a href="https://ru.wikipedia.org/wiki/пђпNoпЈяЃпЎпЊ_пNoп№яЂп№пЄпЎпЊяЃпЎпЃ">https://ru.wikipedia.org/wiki/Список_парадоксов</a> 11. Путенихин П.В. Логика противоречий. - Саратов: "АМИРИТ", 2017. - 133 с., илл., URL: <a href="https://www.elibrary.ru/item.asp?id=42733187">https://www.elibrary.ru/item.asp?id=42733187</a> <a href="https://www.twirpx.org/file/3089642/">https://www.twirpx.org/file/3089642/</a> 16.22.2017 | |
| Категория: Разное | | | |
| Просмотров: 1771 | Загрузок: 525 | |
| Всего комментариев: 0 | |