Путенихин П.В. Правила счета элементов бесконечного множества, ч.2
| [ Скачать с сервера (1.61 Mb) · Скачать удаленно (1,61 Mb) · Скриншот ] | 28.05.2021, 19:17 |
Часть 2 - URL: http://moianauka.ru/load/2-1-0-1509 Часть 3 - URL: http://moianauka.ru/load/2-1-0-1510 ЧАСТЬ 2 Аннотация Вскрыты ошибки Кантора и его последователей в логических рассуждениях о бесконечных множествах. Приведено доказательство счетности континуума, счетности всех действительных чисел. Показана ошибочность рассуждений в задаче об "Отеле Гильберта". Rules for counting elements of an infinite set. The mistakes of Cantor and his followers in logical reasoning about infinite sets are revealed. The proof of the countability of the continuum, the countability of all real numbers is given. The erroneousness of reasoning in the problem of "Hilbert's Hotel" is shown. Оглавление ЧАСТЬ 1 Связь математики и физики Равномощные множества чисел Количества натуральных чисел в группах О счетности континуума - точек на отрезке Задача об "Отеле Гильберта" ЧАСТЬ 2 Несостоявшаяся перепись Разрядность и количество чисел в массиве Счетность всех мыслимых видов чисел О равномощности отрезка и квадрата ЧАСТЬ 3 Стереографическая проекция Литература Несостоявшаяся перепись Парадокс отеля оказался настолько интересным и показательным, что он получил дальнейшее развитие, которое описано, например, в виде шутливого научно-фантастического рассказа от имени вымышленного персонажа: "Из треста космических гостиниц пришел приказ составить заранее все возможные варианты заполнения номеров. Эти варианты потребовали представить в виде таблицы, каждая строка которой изображала бы один из вариантов. При этом заполненные номера должны были изображаться единицами, а пустые нулями. Например, вариант 101010101010... означал, что все нечетные номера заняты, а все четные пустые, вариант 11111111111... означал заполнение всей гостиницы, а вариант 000000000000... означал полный финансовый крах -- все номера пустовали" [9, с.70-71]. Этот фрагмент, цитата является продолжением рассказа об "Отеле Гильберта", для случая бесконечного числа отелей с бесконечным числом номеров и бесконечным множеством гостей. В продолжении рассмотрен еще один из вероятных парадоксов, возникающих в таком тресте отелей. Итак, форма отчета определена. Далее определяется способ его составления: "Директор был перегружен работой и поэтому придумал простой выход из положения. Каждой дежурной по этажу было поручено составить столько вариантов заполнения, сколько номеров было в ее ведении. При этом были приняты меры, чтобы варианты не повторялись. Через несколько дней списки были представлены директору, и он объединил их в один список" [там же] К сожалению, способ описан недостаточно четко, например, что представляют собой "принятые меры", поэтому с учетом предыдущей информации из книги проясним некоторые детали. Фраза определённо противоречива. Изначально под вариантом подразумевалось одно единственное двоичное число, каждый разряд которого относится только к одной комнате. Если же дежурный составляет много вариантов, то неясно, чем они могут отличаться друг от друга? Вернее, ясно, что все они - это один и тот же вариант, одно и то же число с битами - признаками занятости номеров. В дальнейшем же под вариантом явно подразумевается номер той или иной комнаты на этаже. На каждом этаже у дежурной по определению должно быть бесконечное, счетное количество номеров. В противном случае вариантов в смысле номеров комнат у неё будет конечное количество, то есть, каждое двоичное число будет иметь вполне определенное число знаков. Например, 10165 нулей и единиц. В этом случае задача имеет однозначное решение при бесконечном количестве гостиниц и этажей, поскольку любая счетная (потенциальная) бесконечность перекрывает любое конечное число вариантов. Но, с другой стороны, если на этаже счетное, то есть, бесконечное количество номеров, то и в этом случае будет получен список вариантов, содержащий все возможные комбинации из бесконечного (счетного) числа нулей и единиц. То есть, и в этом случае задача решается однозначно, то есть, список вариантов будет единственным и полным. "-- Могу ручаться, что список неполон. Я берусь указать вариант, который наверняка пропущен" [3, с.70-71]. Вполне ожидаема подмена понятий, но её следует показать непосредственно, явно. "Мы заключили пари. Чтобы выиграть его, я предложил прибить каждый вариант на дверь того номера, которому он соответствовал..." [там же]. Сразу же возразим. Напомним читателю, что вариантов составлено столько, сколько номеров на этаже, а не в гостинице целиком. Список отсортирован по возрастанию, но это не имеет принципиального значения, поэтому просто отбросим варианты других этажей, поскольку и одного этажа окажется вполне достаточно. "А потом я поступил очень просто. Подойдя к двери первого номера, я увидел, что соответствующий вариант начинается с цифры 0. Немедленно в блокноте появилась цифра 1; это и была первая цифра варианта, который мне хотелось составить" [там же]. Здесь заметна некоторая неопределенность. Гостиниц - бесконечное число (счетное). Можно также предположить, что, соответственно, этажей и комнат на каждом этаже также счетное (потенциально бесконечное) множество. В этом случае смысл первого номера становится неясен. Нумерация ведётся сквозная? Или в каждой гостинице есть свой первый номер? С этажами тоже не совсем ясно, хотя и проще, поскольку по принятой практике первая цифра номера комнаты равна номеру этажа. И вновь примем решение в пользу рассказчика: отбросим все номера кроме номеров на единственном этаже единственной гостиницы, а в номере комнаты отбросим цифры этажа. Следовательно, на каждом этаже каждой гостиницы будет комната с номером 0, причём под "вариантом", очевидно, подразумевается именно номер комнаты. "Когда я подошел к двери второго номера, то первая цифра соответствующего варианта меня не интересовала, ведь первая цифра моего варианта была уже написана. Поэтому все внимание было обращено на вторую цифру. Увидев, что эта цифра 1, я записал в своем блокноте цифру 0. Точно так же, обнаружив, что третья цифра варианта, прибитого к двери третьего номера, тоже 1, я записал в блокноте цифру 0. Вообще, если я обнаруживал, что n-я цифра n-го варианта есть 0, то писал в своем блокноте на n-ом месте цифру 1, если же n-я цифра n-го варианта была 1, то я писал у себя 0. Когда я обошел все номера гостиницы, то в блокноте оказалась записанной последовательность нулей и единиц" [3, с.70-71]. Методика понятна и разумна, но верные ли выводы из неё делает рассказчик? "-- Вот, полюбуйтесь на пропущенный вариант. -- А откуда известно, что он пропущен? -- Он не может быть первым, так как отличается от него первой цифрой, не может быть вторым, так как отличается от него второй цифрой, третьим, так как отличается от него третьей цифрой, и вообще n-м, так как отличается от него n-й цифрой" [там же]. Как видим, метод полностью совпадает с рассмотренным выше, поэтому также ведет к неверному выводу. В его списке номер начинается, например, с цифры 0. Но это всего-навсего первый разряд бинарного числа бесконечной длины. Можно уверенно заявить, что вся монотонная бесконечная последовательность нулей и единиц в точности содержит половину начинающихся с нуля. Например, пятизначное двоичное число: 00000, 00001, 00010, 00011, 00100 и так далее содержит всего 32 числа, первые 16 из которых начинаются с нуля. Следовательно, если номер первой комнаты начинается с нуля, то номер второй комнаты тоже будет начинаться с нуля. И так на бесконечном количестве дверей. Поэтому в блокноте вторая цифра, как и первая, так же будет единицей. И третья. И четвертая. И так до бесконечности. Счетной. Но как же так?! Получается, что все комнаты будут иметь один и тот же нулевой номер?! Нет, разумеется. Просто длина последовательности нулей и единиц такова, что прочитать последнюю цифру рассказчику не удастся никогда. Вернее, за бесконечное (счетное) количество времени. "... стало ясно, что какое бы счетное множество вариантов ни взять, всегда найдется вариант, не вошедший в это множество... А это и значит, что множество всех вариантов заполнения гостиницы несчетно..." [3, с.70-71]. Как видим, вывод о несчетности вариантов явно ошибочен. Похоже, что этого не заметили и программисты или математики в тресте космических гостиниц, которые обязаны были предостеречь руководство от такого тривиального, бессмысленного задания. Бесконечное (счетное) число вариантов бинарных чисел даёт весь натуральный бинарный ряд чисел. Без пропусков и повторов. Каждый дежурный по этажу должен был составить список всех вариантов (то есть, номеров комнат) из бесконечной последовательности бинарных чисел. Неважно, что дежурных много, а гостиниц - вообще бесконечное (счетное) количество. Каждый из дежурных предоставит в точности один и тот же список вариантов (номеров). По поводу "отсутствующего" номера комнаты добавим - этот номер в списке есть, но находится среди номеров второй половины бесконечного их количества. Заметим, что при таком способе "нахождения" не проходит и хитрость с отбрасыванием ведущих нулей, то есть: 0, 1, 10, 11, 110, 111, 1110, 1111, 11110 и так далее, поскольку в этом случае у второй комнаты в номере отсутствует вторая цифра, у третьей - третья, у четвертой - четвертая и так далее. Разрядность и количество чисел в массиве Легко показать, что причина ошибки заключается в том, что при поиске отсутствующего числа по непонятной причине количество разрядов чисел (записей в блокноте) приравнивалось общему количеству всех чисел. В сущности, это очевидное и даже тривиальное некорректное допущение, и почему оно оказалось незамеченным, непонятно. Действительно, общее количество чисел, их основание и разрядность связаны простым соотношением 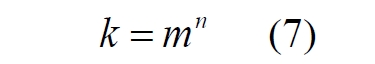 где k - количество чисел разрядности n и основанием m; m - основание чисел: десятичные, двоичные и т.д.; n - разрядность чисел, числового ряда. Например, общее количество чисел с основанием 10 (десятичные) и разрядностью 5 равно 100 000, то есть, от 00000 до 99 999. А количество чисел с основанием 2 (бинарных) и числом разрядов 16, соответственно, равно 216 - или 65 536 чисел от 0000 0000 0000 0000 до 1111 1111 1111 1111. Точно такие же соотношения можно составить и для любых других оснований - шестнадцатеричного, восьмеричного и так далее. Рассмотрим массив бинарных чисел, использованных в "блокнотном методе", и возможность метода определить число, номер, не использованный при нумерации комнат. Сначала вновь обратимся к примеру с массивом пятизначных чисел, теперь уже двоичных, бинарных. Обобщённо в двоичном коде пятизначное число можно записать как nnnnn c диапазоном от 00000 до 11111. Количество этих чисел равно 25 = 32. Поскольку их относительно мало, можем записать все их в виде таблицы 4х8 - слева направо, сверху вниз:  Теперь можно воспользоваться "блокнотным методом". Рассказчик и его герой в рассказе, а также все их последователи искали пропущенное число поразрядно, то есть, переходя от двери к двери комнат отеля, добавляли к записи в блокноте всё новый и новый разряд, полагая, что тем самым они просмотрели все возможные числа, номера комнат. Но на самом деле, как видно из соотношения, они переберут только количество чисел, равное их разрядности. Мы, согласно традиции метода, предполагаем, что кому-то удалось пересчитать и перенумеровать все 32 числа в этой таблице. Попробуем доказать, что счётчик всё-таки пропустил, по меньшей мере, одно число. Итак, смотрим на первое число. Его первый разряд равен нулю, поэтому записываем в блокнот единицу: 1nnnn. Остальные четыре цифры нам пока неизвестны. Теперь смотрим на второе число, двигаясь по таблице сверху вниз. Видим, что вторая цифра второго числа равна единице, поэтому записываем в блокнот цифру 0 вторым разрядом нашего числа: 10nnn. Смотрим третье число и видим, что третья цифра равна нулю. Делаем запись в блокнот: 101nn. Таким же образом записываем и четвёртую цифру 1 в блокнот, заметив, что четвёртая цифра четвёртого числа в таблице равна нулю: 1011n. Последнее, пятое число в таблице берём рядом с предыдущим: последнее число в следующей колонке. В результате получаем в блокноте окончательно число 10110. Согласно "блокнотному правилу" наше число отличается от первого первой цифрой, от второго - второй, от третьего - третьей и так далее. Следовательно, мы должны сделать вывод, что счётчик не пронумеровал это число в процессе подсчёта, ведь оно отличается первым разрядом от первого числа... и так далее. Однако... это явно не так. Реально мы просмотрели только 5 (пять) чисел в колонках, хотя общее количество чисел равно 32 - в 6 раз больше. И это, якобы пропущенное число, в этой таблице точно есть. Находится оно в третьей строке в седьмой колонке. Заметим, что порядок просмотра номеров в таблице значения не имеет, просто будут получены разные "пропущенные" номера. Еще раз отметим, что метод просматривает совсем даже не все числа, а только их количество, равное разрядности числа. Но ведь по условиям рассказа об отелях номеров на этаже - бесконечное количество, то есть, разрядность каждого числа также равна бесконечности. Тем не менее, это ровным счетом ничего не меняет, в этом случае герой рассказа точно так же просмотрит не все числа, а только их часть, и найденное им якобы отсутствующее число обязательно будет присутствовать среди чисел, до которых он просто никогда не дойдёт. Как говорится, что-то пошло не так. А не так пошло использованное "блокнотное правило". Мы в рассматриваемом общем массиве чисел можем, имеем право просмотреть только 5 (пять!) чисел. Любое следующее число обязало бы нас приписать к "найденному" числу ещё один разряд, но в нашем массиве нет 6-разрядных чисел. Отношение разрядности чисел к их количеству (7) в массиве описывается простым уравнением: 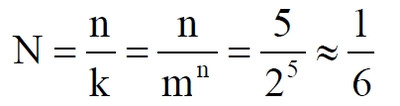 Здесь n - это основание массива: в нашем случае бинарных чисел m = 2. Для десятичных чисел основание m = 10, для шестнадцатиразрядных hex-чисел m = 16. Соответственно, n - это разрядность чисел, в нашем случае n = 5, следовательно, N ≈ 1/6. Используя это уравнение, мы можем определить соотношение N и для других, например, для 10-разрядных бинарных чисел: 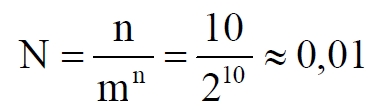 Замечаем, что при увеличении разрядности чисел отношение уменьшается. В пределе, какой рассматривается в задаче об отеле Гильберта, разрядность чисел - номеров комнат в отелях стремится к бесконечности. 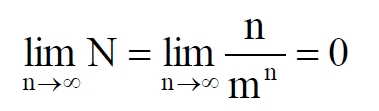 Это означает, что при бесконечном количестве комнат счётчик может просмотреть хотя и бесконечное их количество, но в общем количестве комнат это просмотренное количество эквивалентно нулю. Получается, что доля просмотренных героем рассказа чисел от общего их количества равна нулю, поэтому нет ничего удивительного, что любое найденное им число обязательно будет присутствовать в их полном наборе. Собственно говоря, это тривиальный, очевидный факт: всё бесконечное множество чисел бесконечной разрядности содержит все возможные числа, то есть, это тождественно весь натуральный ряд чисел, поэтому "отсутствующих" чисел в нём быть не может просто по определению. Такой же результат будет получен, если рассматривать не разрядность, а общее количество чисел. 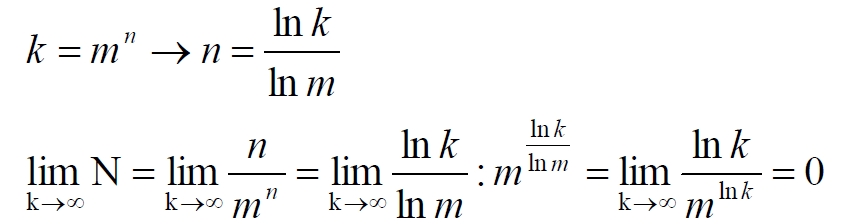 Следовательно, каким бы большим ни был найденный им номер комнаты, якобы не получившей порядкового номера, номера всех комнат используют все без исключения числа от нуля до бесконечности, то есть, содержать все возможные порядковые номера, среди которых обязательно присутствует и "пропущенный" номер. Таким образом, вывод о несчетности вариантов, номеров комнат является ошибочным. Похоже, что и в управлении космических гостиниц тоже не нашлось грамотного программиста или математика, которые могли бы объяснить директору ошибочность вывода о неполноте списка, и что пари выиграл именно он, директор. Счетность всех мыслимых видов чисел Теперь еще раз обратимся к утверждению о несчетности континуума. Действительные числа являются лишь частью ряда возможных чисел, включающих в себя вещественные, комплексные, кватернионы, гиперкомплексные, поличисла (коммутативно-ассоциативные гиперкомплексные числа), разнообразные многомерные и любые иные виды чисел. Здесь нас не должны интересовать алгебры этих чисел и их свойства. Единственное не обязательное условие - это конечная длина записи числа. То есть, запись числа в виде бесконечного ряда коэффициентов мы пока оставим без внимания, указав, что задача решается так же - предельным переходом. Все мыслимые числа в общем виде можно записать, например, в следующем виде 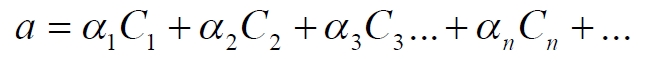 где α - любое вещественное число; С - любой индекс, например, мнимая единица i. Например, число может иметь вид a = 2,71828... -действительное число, или a = 3+2i - комплексное число, или a = 5+2i+3j+8k - кватернион. Правильно организованный способ подсчета этих чисел позволяет показать счетность всего их ряда. Вообще-то, такой результат является простым следствием принятого способа подсчета. На классический вопрос "сколько будет дважды два?" известен шутливый ответ: а сколько надо? По большому счету, всё сводится к спору о том, какой способ подсчета лучше или правильнее. Рассмотрим следующий способ записи всех действительных чисел: запишем после запятой все последовательные натуральные числа "задом наперед", а до запятой - в каждом ряду возрастающие натуральные числа на всём числовом диапазоне. Возникает, например, такой фрагмент последовательности действительных чисел: 0,699?0,799?0,899?0,999?0,0001 и так далее. Последовательность чисел в таблице будет содержать все без исключения числа. Собственно правило формирования чисел имеет простое аналитическое выражение, подобное (3) или (6). Возьмем два натуральных числа m и n, изменяющиеся от 0 до бесконечности. Запишем с их помощью некоторое число в виде 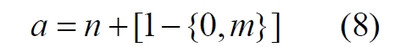 Здесь запись {0,m} означает число, меньшее единицы, дробной частью которого является натуральное число m. Фактически при табличной записи чисел n является номером строки в таблице, а m - номером колонки. Например, в ячейке (n=3; m=5) будет находиться число:  а в ячейке (n=10; m=2021) будет находиться число 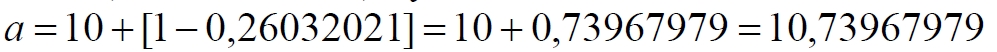 Для составления таблицы начнем перебирать, подсчитывать все получившиеся числа. Строки чисел будут иметь вид: 0,0+0,9+0,8...+0,1+0,90+0,89+0,88...+0,81+0,80+0,79 ... +0,12121... ,0+1,9+1,8...+1,1+1,90+1,89+1,88...+1,81+1,80+1,79 ... +1,12121... ,0+2,9+2,8...+2,1+2,90+2,89+2,88...+2,81+2,80+2,79 ... +2,71828... ,0+3,9+3,8...+3,1+3,90+3,89+3,88...+3,81+3,80+3,79 ... +3,14159... ,0+4,9+4,8...+4,1+4,90+4,89+4,88...+4,81+4,80+4,79 ... +4,12121... Знаки плюс в таблице означают не суммирование, а используются как разделитель между числами. В связи с повторами, поскольку числа вида 0,1+0,10+0,100+0,1000 в использованном алгоритме считаются разными, общее количество чисел, видимо, окажется больше примерно на 10%. Конечно, мы можем повторяющиеся числа пропускать, не считать, но 10% погоды, как говорится, не делают. Если изобразить расположение чисел на графике, то график будет иметь вид пилы. Для большей общности можно добавить еще одно условие: четные числа n будем делить на 2 и полученное число записывать согласно выбранному виду. Для следующего нечетного числа n запишем то же самое число, только со знаком минус. Очевидно, что в такой ряд легко включить и все вещественные и действительные, комплексные числа и даже кватернионы. Нумерация сформированных чисел соответствует нумерации членов любого числового ряда, то есть, каждое число из таблицы получит свой индивидуальный натуральный порядковый номер, будет пронумеровано при подсчёте. Каким бы ни было количество всех действительных чисел, наше движение по ряду не пропустит ни одного из них, и каждое из них получит свой индивидуальный натуральный номер. Таким образом, можно сделать вывод: континуум является счетным. Используя обратный метод индексации Кантора [3, с.77], мы можем корректно включить в этот континуум все мыслимые виды чисел. Как известно, метод Кантора формирует новое число из двух следующим образом: 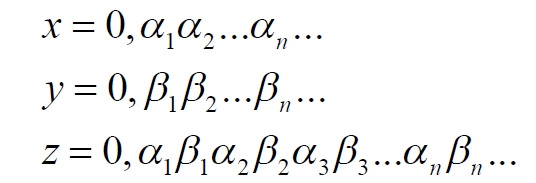 У двух рациональных чисел x и y берутся цифры после запятой и поочередно вписываются после запятой третьего числа z. Мы проделаем обратную операцию, сформируем из одного числа несколько коэффициентов, например, для кватерниона. Возьмем из полученного ряда какое-либо число z и будем рассматривать его как составное, отбросив ноль и запятую: 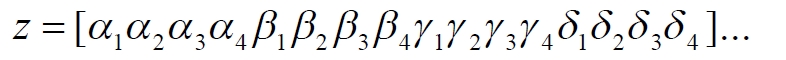 Очевидно, что все составляющие число цифры гарантируют любую комбинацию, поскольку ряд чисел z бесконечен. Теперь составим из одноименных цифр новое число, кватернион: 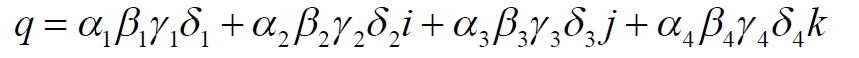 Здесь в каждом коэффициенте показаны только четыре цифры, но, очевидно, их может быть любое количество. Также очевидно, что и самих коэффициентов может быть любое число: один коэффициент даёт действительное или вещественное число, два коэффициента дают комплексное число и так далее. Понятно, что полученный ряд всех возможных чисел является счетным, каждое из исходных чисел имеет свой индивидуальный натуральный порядковый номер. Среди этих чисел обязательно окажутся и число е (2,71828...), и π (3,14159...), и константа пропорциональности С (0,76422...) Ландау - Рамануджана, и постоянная тонкой структуры α ≈ 1/137, причем с бесконечной точностью. Счетность ряда обеспечивается использованием метода квадратов, предложенного математиком-филателистом из рассказа об отелях с бесконечным числом номеров [3, с.57] являющегося эквивалентом диагонального процесса Кантора: 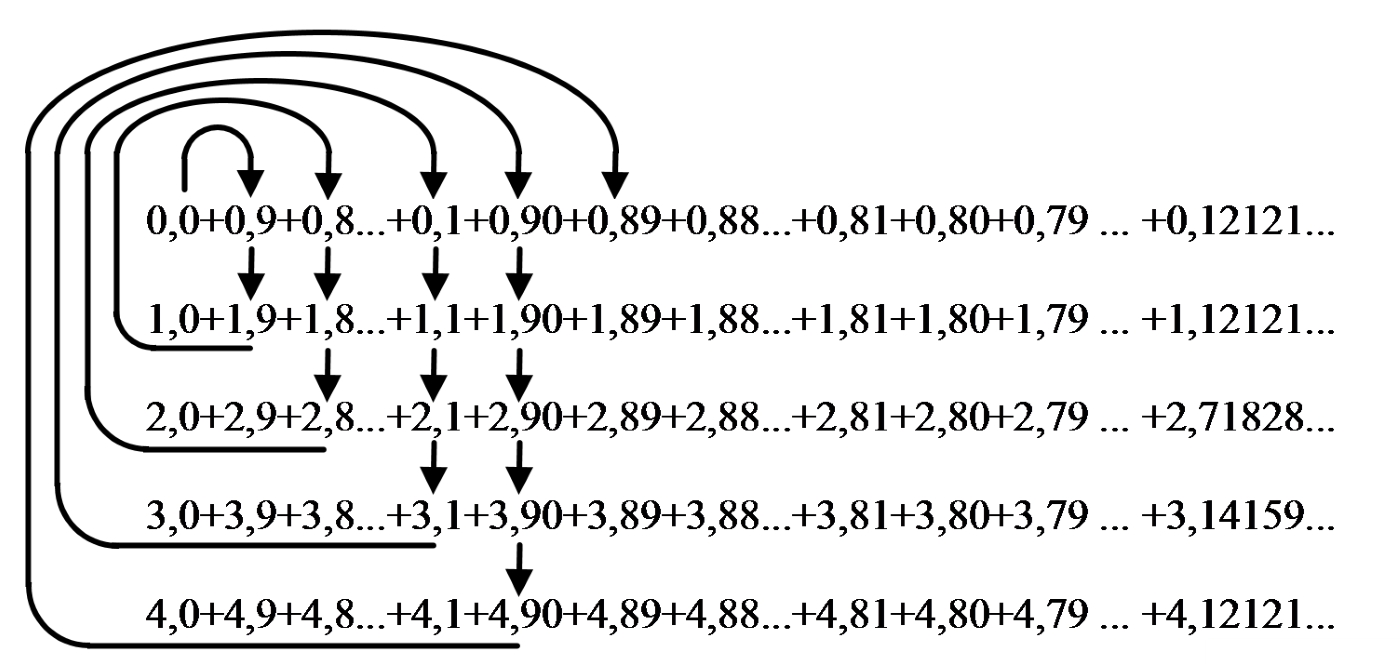 Метод мы будем использовать в точности, как в рассказе, поэтому числа из приведенной выше таблицы расположатся друг за другом и получат соответствующие номера примерно в следующей последовательности: 0,0+0,9+1,9+1,0+0,8+1,8+2,8+2,9+2,0...+0,1+1,1+2,1+3,1+3,8+... Здесь знак плюс между числами также является простым разделителем, вместо пробела или запятой. Мы приводим только положительные числа, но, как отмечено выше, таблица содержит все вещественные, действительные и прочие числа. Порядок их подсчета соответствует правилу нумерации членов ряда, то есть, каждое число из таблицы получит свой индивидуальный порядковый номер, то есть, будет пронумеровано. О равномощности отрезка и квадрата К таким же ошибочным выкладкам следует отнести и известное доказательство Кантора равной мощности точек в прямом отрезке и квадрата со стороной, равной этому отрезку. На самом деле мощность множества точек квадрата на отрезке имеет более высокий порядок, чем мощность множества точек отрезка. То есть, больше в бесконечное, счетное число раз. Есть наглядный и предельно простой способ показать это: нужно отрезок просто наложить на квадрат. Под отрезком окажутся все тождественные ему точки квадрата. Остальные точки квадрата образуют отдельное бесконечное множество точек, очевидно, большей мощности. Если же отрезок длиннее стороны квадрата, то, казалось бы, можно найти такой квадрат, который будет содержать меньше точек, чем эта линия: "Разумеется, можно разломать прямую линию на отрезки, длина которых равна стороне квадрата, и после этого каждый отрезок поместить в квадрат так, чтобы они не пересекались друг с другом" [3, с.59]. Это верно, но ломать линию совсем не обязательно. В доказательстве Кантора длина линии равна стороне квадрата. Однако, может быть, разлом линии в цитате предложен для того, чтобы завуалировать, спрятать фактическое опровержение этого доказательства? Действительно, если наложить отрезок на квадрат, то их точки будут отождествлены, причем, вопреки Кантору, у квадрата точек окажется несопоставимо больше, чем у линии. Как бы то ни было, в цитате отчетливо просматривается мысль, что линия содержит меньше точек, чем квадрат. По аналогии с таким разбиением возникло и обратное предположение: "Но вдруг и квадрат можно как-то разбить на части, а потом эти части положить на прямую, чтобы они не задевали друг друга?" [3, с.59]. Алгебраически с учетом равной метрики, как показано выше, это возможно: вытянуть квадрат в линию. Такой способ совмещения, алгебраический сразу же высвечивает противоречивость решения Кантора. К сожалению, автор цитаты не стал развивать эту идею дальше. Для сравнения двух множеств точек следует попытаться установить однозначное соответствие между этими точками, то есть, показать, что точки обоих этих множеств можно объединить, скажем, в пары (a, b), такие, что каждый элемент, каждая точка a принадлежит линии, а каждый элемент, точка b - квадрату, причем каждый из элементов a и b попал только в одну пару [3, с.59]. Согласно Кантору два бесконечных множества - точки линии и квадрата - имеют одинаковое количество элементов, если между этими элементами можно установить указанное однозначное соответствие. В математике обычно говорят о мощности множества, подразумевая под нею количество его элементов. Следовательно, отрезок и квадрат, построенный на нем, по Кантору имеют одинаковую мощность. Для доказательства этого он использует следующий метод. В системе координат x0y простроен квадрат ABCD, причем точка A совпала с началом координат, а точка B лежит на оси x. Не всякий способ позволяет установить взаимное однозначное соответствие между точками квадрата и отрезка: "Проектирование точек квадрата на отрезок АВ здесь не помогает, ведь при проектировании в одну точку отрезка перейдет бесконечное множество точек квадрата (например, в точку А -- все точки отрезка DA)" [3, с.77]. Однако такое обоснование нас, разумеется, устроить не может, поскольку это решение верное, но оно все-таки отбрасывается. Координаты каждой точки квадрата можно представить в мнемоническом виде:  В этих записях каждый символ α, β представляет собой какую-либо цифру из 0...9. То есть, x и y - это просто два дробных числа, меньшие единицы. Здесь следует, кстати, выразить недоумение по поводу отождествления чисел вида 0,50000... и 0,499999.... "...например, 0,500000... и 0,49999999...-- это одно и то же число. Для определенности будем пользоваться записью с нулями" [3, с.73]. В частности, вопрос: отождествляются только такие числа? А, например, числа 0,550000... и 0,549999... не отождествляются по такому же принципу? Это правило, собственно говоря, не выдумка. Например, его использует офисная программа MS Excel, правда, с противоположной "определенностью". Там любое целое число в одном из представлений так и записывается: с множеством девяток в конце. Но в нашем случае мы рассматриваем числа в их абсолютном смысле. Поэтому число 0,5000...1 и число 0,5, число 0,4999999... или даже 0,4999...9998 - это совершенно разные числа. Если же вводить указанное правило (округление), то следовало бы и здесь дать веские обоснования, почему такой участи избежали числа 0,549999... или 0,22229999..... Чем они кардинально отличаются? Если же правило распространить и на них, то сразу же образуется счетная бесконечность чисел, отброшенных в результате безосновательного округления. Итак, после тривиального преобразования координат точки квадрата в мнемоническую запись, с ними производится манипуляция, которая также не имеет веско аргументированного, рационального смысла. Перетасовыванием знаков двух чисел формируется новое число: 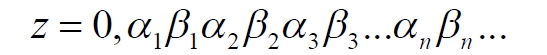 Обратим внимание на следующее интересное замечание и на приведенный далее способ отождествления: "для простоты мы не берем точки квадрата, лежащие на его сторонах, а берем лишь внутренние точки... Нам надо теперь найти точку Q отрезка АВ, соответствующего точке Т" [3, с.78]. Для "простоты" - это, прямо скажем, - лукавство. Этим упрощением отбрасывается неразрешимое противоречие совпадения линии и стороны квадрата. Точка T - это точка в квадрате с указанными координатами x и y. Координата точки отрезка выбирается по принципу Q = z. Далее делается ожидаемый вывод: точке T квадрата поставлена в соответствие точка Q отрезка [0, 1]. Следовательно, всем различным точкам квадрата соответствуют разные точки отрезка и тем самым установлено взаимно однозначное соответствие между точками квадрата и точками отрезка. Из этого также делается вывод, что множество точек квадрата имеет такую же мощность (количество), что и множество точек отрезка (их количество). Такие выводы противоречат не только здравому смыслу, но и логике, поскольку налицо подмена понятий. Сначала обратим внимание на то, что же отождествляется. А отождествляется координата точки отрезка и некоторое комбинационное число, которое вообще-то координатой не является. Действительно, координатой чего мы можем признать сборку - число z? Какое отношение эта комбинация знаков имеет к координатам x, y точки квадрата? Координаты - это два числа (так сказать, две штуки), а z - это одно число (одна штука). По существу, число z является для координат x, y своеобразным индексом. Иными словами, мы здесь отождествили не две точки, а точку и некий индекс. Но индекс чего? Квадрат - это плоская фигура, следовательно, каждая его часть изначально должна рассматриваться как такая же плоская фигура, фигура с площадью. И мы фактически отождествили не две точки, а точку и площадку, бесконечно малый квадрат. Размеры точек на линии и точек, площадок на квадрате разные, хотя и те и те бесконечно малы. Конечно, для отождествления это не является противоречием. Мы можем, например, отождествить 10 яблок и 10 уток. Или 200 кресел в кинотеатре и 200 зрителей. Но при этом следует помнить, что равны не они сами по себе, а их количества. В доказательстве Кантора, вроде бы, так и говорится, что равны мощности, равны количества. Однако преподносится это так, что создается впечатление, будто эти сравниваемые множества равны не только по своим количествам, мощности, но и равны буквально - точка на линии тождественно равна точке на квадрате. При таком подходе можно отождествить любые бесконечности, просто отбросив их качество и оставив лишь безликое количество. Все зависит только от искусства отождествителя. Приведём простой пример. Точки любой линии на плоскости характеризуются двумя координатами. Точно так же и в рассмотренном примере все точки линии имеют две координаты, одна из которых просто равна нулю. Теперь становится ясным, почему мы обратили внимание на замечание "для простоты мы не берем". На самом деле в таком упрощении преследовалась цель упростить организацию подмены понятий. Ведь если у линии признать наличие имеющейся на самом деле второй координаты, то и для неё пришлось бы также формировать комбинированное число - индекс. Действительно, если вернуть в рассмотрение и стороны квадрата, то одна из них совпадет с отождествляемой линией. В этом случае надо было бы веско обосновать, почему координаты нижней стороны квадрата преобразуются в число z, а линия, полностью совпадающая с этой стороной, по-прежнему описывается одной координатой, хотя у неё однозначно имеется и вторая, нулевая? Ясно, что разумные обоснования этого просто невозможны. Если же вернуть линии её законные права на вторую, нулевую координату, то все её собственные числа z будут начинаться с нулевого знака. То есть, с линией можно будет отождествить только одну единственную линию квадрата - его нижнюю сторону. Соответственно, мощность множества точек линии окажется меньше мощности точек квадрата в счетное число раз, то есть, в бесконечное. Мощность множества точек квадрата имеет более высокий порядок. Просто результат зависит от способа подсчета и может быть на любой вкус. Два способа мы уже увидели. Рассмотрим еще один. Рассмотрим эти два объекта в единой метрической системе единиц, в которой размер точки квадрата равен размеру точки линии. Это естественное разумное предложение: бессмысленно приравнивать, скажем, два куска золота, размеры которых неизвестны. Длина стороны квадрата равна a, следовательно, метрически он содержит a2 точек. Отрезок по этой же причине содержит a метрических точек. Другим словами, квадрат и линия метрически тождественны. Тогда линия длиной na будет содержать заведомо больше точек, чем квадрат, если n > a. Такой же результат можно получить и иначе. Возьмем тот же квадрат и разделим его на 4 части. Нижний ряд, два вновь образовавшихся квадрата назовём условно линией. Пока эти два квадрата, понятно, на линию не похожи. Теперь разделим эти 4 квадрата ещё на 4 части каждый. Нижний ряд из 4 квадратов по-прежнему будем считать линией. Затем вновь каждый квадрат разделим крестом на 4 части. Теперь уже нижний ряд из 8 мелких квадратов отдаленно напоминает некую линию. Посчитаем, отношение количества этих квадратиков в исходном квадрате к их количеству на прообразе линии. По пройденным шагам деления эти отношения равны: 2, 4, 8. Легко обнаружить, что эти отношения будут возрастать по мере дальнейшего деления квадратов по уравнению 2n в 2n. Каждый из сомножителей означает, соответственно, деление по вертикали и по горизонтали. Продолжим такое же деление до бесконечности: n → ∞. Очевидно, что все квадратики станут бесконечно малыми, превратятся в точки и исчезнут из видимости. При этом и линия станет тем, чем мы её обычно и представляем - линией с нулевой толщиной. Что важно, в этом случае и квадрат и линия состоят из одинаковых точек. И количества этих точек будут для квадрата - 2n в 2n, для линии - 2n. Отношение количеств или мощностей точек квадрата к точкам линии будет равно 2n. При увеличении числа шагов деления до бесконечности отношение также увеличится до бесконечности. Это значит, что мощность множества точек квадрата имеет более высокий порядок, чем мощность множества точек отрезка. Конечно, этот способ относится более к алгебре, чем к геометрии, но поэтому в нём и подмены с отождествлением скрыть труднее. Наконец, можно рассмотреть и классический способ подсчета. Для этого возьмем одну из горизонтальных линий квадрата и начнем пересчитывать на ней точки: 1, 2, 3 и так далее. Поскольку координаты точек на отождествляемой линии совпадают с одноименными координатами линии квадрата, то будет пересчитывать одновременно и их: 1, 2, 3 и так далее. Очевидно, что мы получим два тождественных счетных множества. Вряд ли этому следует удивляться, физически и геометрически две линии тождественны. Следует отметить, что здесь мы пересчитываем не координаты, которые обозначаются действительными числами, необоснованно признанными несчетным множеством. После завершения счета мы обнаруживаем, что одна единственная линия квадрата и отождествляемая с ним линия имеют равные мощности или количества точек. Но на квадрате таких линий - счетное множество (помним и отвергаем утверждение о несчётности действительных чисел). Следовательно, общее число точек на квадрате в счетное множество раз превышает число точек на любом его отрезке и отождествляемой линии. Однако все рассмотренные отождествления, зависимые от способа счета, построены таким образом, что подсчет числа точек всегда приводит к результату либо большей, либо равной мощности множества точек квадрата по сравнению с множеством точек отрезка. Но можно подобрать и такое правило счета, что соотношение изменится на обратное: окажется, что число точек в отрезках является более мощным множеством. Для этого возьмем не один, а несколько одинаковых квадратов, просто выбрав в кубе несколько разных сечений, и одну линию с длиной ребра куба. Попробуем отожествить все точки этих квадратов с точками на линии. Вновь воспользуемся методикой нумерации точек, предложенной Кантором. Согласно ей, для того чтобы точки на квадратах можно было различить и из очевидных соображений мы обязаны признать, что квадраты имеют ещё одну координату. То есть, каждая точка квадрата в кубе в этом случае характеризуется тремя координатами: 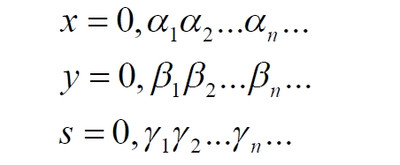 Для простоты, что, вообще-то, усложняет наше опровержение, ослабляет его, возьмём значения этих координат в кратчайшем виде, в виде единственной цифры от 0 до 9 без последующих дополнительных нулей, что во много раз увеличит число таких комбинированных точек, принадлежащих каждому квадрату. Для определенности возьмем в кубе 10 сечений, причем имеющие точное значение координаты s = 0; 0,1; 0,2 ... 0,9. Теперь создадим по методу Кантора новые числа для точек каждого квадрата. Согласно этому методу каждая точка квадрата будет описываться новым числом - индексом. Исходные координаты задаём в следующем формате: 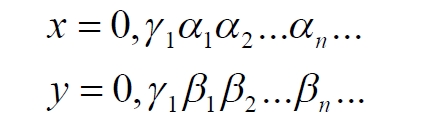 из которых формируем индекс: 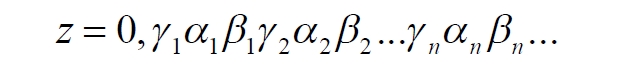 Здесь символом γ обозначен номер квадрата или, что то же самое, его координата в исходном кубе. Например, точки квадрата с номером s = 0,5 будут описываться индексом: 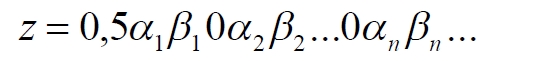 Как видим, закономерно и оправданно все точки и, соответственно, скомбинированные числа отличаются друг от друга, а все точки этого квадрата расположатся на интервале 0,5...0,6 отождествляемой линии и, более того, на линии останется бесконечное число точек, которым не будет соответствовать ни одна точка этого квадрата. Это точки, для которых индекс должен был бы содержать вместо нулей в позициях, кратных трём, другие цифры. Ничего не изменится, если цифру координаты s ставить в тройках последней. Такая же ситуация будет наблюдаться с индексами и других девяти квадратов. Легко обнаружить, что комбинированные числа каждого квадрата изменяются в диапазонах, соответственно, [0, 0.1), [0.1, 0.2), [0.2, 0.3) и так далее. Таким образом, мы разместили все точки десяти квадратов на одной линии [0, 1]. Получается, что мощность множества, количество точек квадрата имеет меньший порядок, чем мощность множества точек любой линии. В нашем случае - в десять раз. Но мы могли использовать и другое количество квадратов. Тогда и их точки оказались бы во взаимном однозначном соответствии с точками части отрезка. В этом случае соотношение мощностей станет еще больше и даже, по желанию, в любое число раз. Очевидно, что такой принцип "сколько будет? а сколько надо?", к которому, по сути, сводится метод Кантора, не может служить основой для корректного математического приема. Но в чем же состоит хитрость, изюминка, так сказать, канторовского метода отождествления? По какой загадочной причине происходит такое противоестественное отождествление? В чем его тайный механизм? Ведь мы же четко видим, что каждой точке квадрата можно однозначно привязать каждую точку линии, причем ни одна из точек не останется без своей единственной пары. А тайна, в сущности, предельно проста. Покажем это на еще одном несколько отвлеченном, но подобном примере. Возьмем для лучшей визуализации квадрат с бесконечным числом точек в количестве... 1000х1000. Конечно, это на самом деле не бесконечность, но число все-таки очень большое - миллион точек, пересчитать которые вручную будет весьма непросто. Выберем на этом квадрате одну линию, нижнюю грань квадрата. Согласно методу Кантора присвоим какой-то точке квадрата индекс: 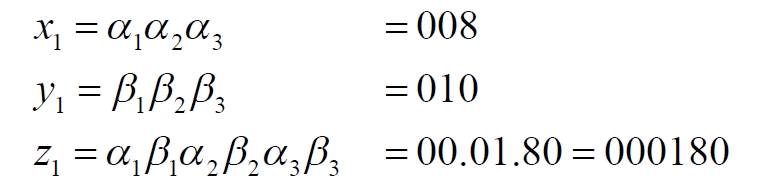 Здесь индекс z сначала представлен с разделительными точками, чтобы было видно, как он образован. Итак, мы получили число z, которое, видимо, точно имеется на отрезке [0, 999]. Правда, настораживает число нулей в этом индексе. Поэтому возьмем для уточнения другую точку на квадрате: 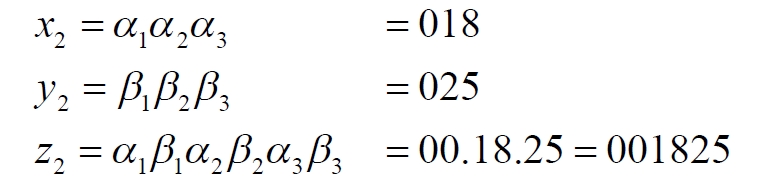 Что-то у нас, как видим, пошло не так. Сразу же можно сделать вывод: на линии [0, 999] такой точки точно нет. В чем же дело? Мы в точности следовали методу Кантора, просто используя отрезок не [0, 1], а более длинный [0, 999]. Принцип тот же, а размеры фигур явно не должны влиять на результат. Иначе получается противоречие: квадрат и линия размером [0, 1] тождественны по мощности, а квадрат и линия [0, 999] имеют уже разные мощности. Однако именно в этом и состоит хитрость, а по сути подмена понятий в методе Кантора. В нашем случае мы можем попытаться решить проблему такой же дополнительной хитростью. Просто добавим в нашем индексе... запятую. В этом случае подозрительно большое количество нулей сразу превращается в нужное количество: 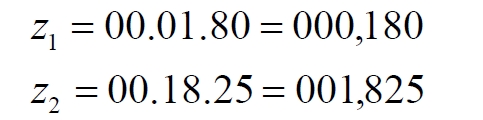 Вот теперь-то каждая из этих точек уже обязана найти своё соответствие на линии. Но возникает другое противоречие. Координаты всех точек квадрата и линии - целые натуральные числа. А здесь мы получили числа дробные, поэтому отождествлять эти индексы с точками линии мы не имеем права. Зато мы обнаруживаем ту самую загадку метода Кантора для отрезка [1, 0]. Фактически индекс формируется методом, схожим с умножением двух чисел. В нашем случае это соответствие должно выглядеть примерно так: 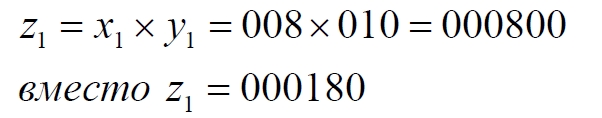 и для второго примера: 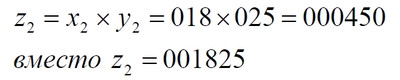 Для сравнения приведем и третий пример: 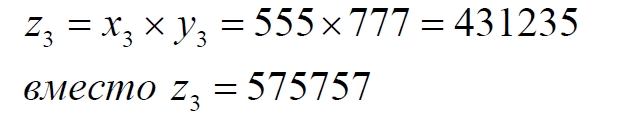 Как видим, оба метода - умножение и перетасовка цифр - дают числа одного и того же порядка с разрядностью площади квадрата (миллион). При этом можно догадаться, что количество разных произведений координат ровно в два раза меньше, чем количество пар сомножителей, поскольку они могут меняться местами. Действительно, пар сомножителей ровно миллион, следовательно, и произведений тоже ровно миллион. Поскольку существуют симметричные пары сомножителей, то их произведения равны. Следовательно, число уникальных произведений равно полумиллиону. Мы полагаем, что произведение разных чисел дают разные результаты. При перетасовках цифр смешиваемых пар также ровно миллион, следовательно, и результирующих чисел с перетасованными цифрами также будет миллион. Но в этом случае, что довольно странно, среди них не будет одинаковых. Иначе говоря, при умножении пар какие-то значения в ряду из миллиона чисел будут отсутствовать. Это легко обнаружить: при перетасовке пар может быть получено число 999 999, но при умножении пар такое число получено быть не может - максимальное значение произведения равно 998 001. И таких "отсутствующих" произведений пар - ровно полмиллиона. Несомненная выгода метода Кантора в том, что каждая точка получит свой индивидуальный, уникальный индекс. Однако остаётся проблема: таких индексов заведомо больше, чем элементов в строке, следовательно, и в отождествляемой линии. Искусственно введенная запятая сжимает эти числа до интервала отрезка [0, 999], но множество из них сразу же становятся дробными, то есть, объективно также не могут этому отрезку принадлежать. Увеличение до бесконечности дискретности квадрата и линии сохранит эту тенденцию без отождествления точек квадрата и линии. А что же с исходным методом Кантора для единичного отрезка? Там, как видим, произведена точно такая же замена умножения двух чисел на перетасовку их цифр, позволившая получить нужное количество индексов. Порядок чисел при умножении и перетасовке по-прежнему один и тот же. Однако индексы или произведения координат имеют больший порядок дискретности, чем каждая из координат, в том числе, и точки отождествляемой линии. И здесь происходит всё та же подмена понятий при подсчете числа элементов в ряду, что и при подсчете числа четных чисел в натуральном ряду. Только здесь каждой точке линии соответствует бесконечное число индексов точек квадрата. И вот почему. Понятно, что в числах с бесконечным числом знаков разглядеть это весьма непросто, тем более что все они выглядят одинаково, поскольку одинаково начинаются - с нуля и запятой после него. Сравнивая числа - координату линии (q) и координатный индекс z(x, y), например, для q=x=y=0,1 (точное значение), мы находим z=0,11. Дискретность z в этом случае в 10 раз выше, чем дискретность q. То есть, между двумя дискретными значениями q=0,1...0,2 поместится десять подобных индексов. Если q=x=y=0,12345, то z=0,1122334455 и дискретность z уже в 100000 раз больше дискретности q. Следовательно, между точками q=0,11223...0,11224 (это точные значения) поместится 100000 индексов с дискретностью z. Другими словами, беря две координаты с некоторой дискретностью (числом знаков после запятой), мы получаем индекс с удвоенной дискретностью и степенным увеличением их количества. Сравнивая координаты линии и индексы, мы сравниваем фактически не их значения, которые предельно скрыты от нас и не могут быть равны, а их порядковые номера, которые для счетных множеств, разумеется, всегда найдут соответствие. Описать этот процесс однозначно и максимально развернуто крайне сложно. Поэтому рассмотрим ещё один пример. Пусть отрезок [0, 1] состоит из миллиарда (109) точек, а соответствующий ему квадрат, следовательно, содержит 1018 точек. Эти числа являются так же и количествами их порядковых номеров, эквивалентами мощностей этих множеств. Сразу же обнаруживаем, что на линии точек меньше, чем в квадрате. Если постоянно удваивать количество точек вплоть до бесконечности, это отношение будет только возрастать. Если для отождествления мы возьмём произвольную точку указанного квадрата, то её координатный индекс будет содержать 1018 знаков после запятой. И мы не имеем никакого права отождествлять этот индекс с точкой на линии, поскольку на ней допустимы только числа с 109 знаков после запятой, точек с такой дискретностью на линии просто нет. При увеличении дискретности квадрата и линии это расхождение будет расти по квадратичному закону. Кстати, здесь мы наглядно обнаруживаем абсурдность сравнивания количества чисел натурального ряда и его части. Мы можем диагональным процессом Кантора тривиально перенумеровать точки линии и точки квадрата, даже не формируя для них индексы, и получим при этом равенство их количества. Однако мы только что увидели, что такое равенство противоречиво, а попросту его нет. Следовательно, и сравнивание количества членов множеств путем их раздельного пересчитывания - это опасный, ошибочный, некорректный метод, позволяющий получить любой желаемый результат, и которым следует пользоваться предельно продуманно. Действительно, мы можем сравнивать точки линии и точки квадрата таким же простым раздельным пересчетом, получив в обоих случаях бесконечность. Но это разные бесконечности, бесконечности разной мощности. Напротив, возьмем какую-либо y-линию на квадрате и начнем пересчитывать на ней точки: 1, 2, 3 и так далее. Одновременно с этими точками будем пересчитывать и точки на линии: 1, 2, 3 и так далее. Мы тем самым однозначно отождествим все точки линии со всеми точками на одной из линий квадрата. Остальные линии квадрата, с другими координатами, разумеется, останутся без номеров. Это самый правильный способ пересчета и отождествления. Итак, даже при ослаблении нашей аргументации мы приходим к выводу, который противоречит выводу Кантора об их равенстве. Два способа нумерации, основанных тождественно на одном и том же методе, приводят к несовместимым, противоположным выводам. Поэтому этот метод Кантора логически неверен, ошибочен. И вновь возникает риторический вопрос, какой же в этом случае метод верный? Методов группировки может быть сколько угодно, поэтому верным является только один метод - без группировки, то есть, сравнивать можно только равнозначные объекты - линию с линией. В этом случае вывод однозначный - множества точек линии и квадрата не равномощны. Самым простым и наглядным способом определения этого является простое наложение линии на квадрат и отождествление соприкоснувшихся точек. Практически такая же противоречивая ситуация возникает и при отождествлении двух противоположных сторон квадрата: верхней и нижней, либо любых двух средних линий квадрата. Возникает совершенно противоестественная ситуации: эти пары линий вообще нельзя отождествить, поскольку нумерация их точек не имеет одинаковых значений. Верхняя сторона квадрата должна иметь по Кантору значения первой цифры после запятой всех точек, начинающиеся с 9, а нижняя - с 0, а средние, например, с 3 и 5. Две явно одинаковые линии оказываются несопоставимыми. Литература 1. Бесконечность, Википедия, URL: <a href="https://ru.wikipedia.org/wiki/п"пЅяЃпЊпЎпҐпЅя‡пҐпЎяЃя‚яЊ">https://ru.wikipedia.org/wiki/Бесконечность</a> 2. Виленкин А., Мир многих миров: Физики в поисках параллельных вселенных Алекс Виленкин, пер. с англ. А. Сергеева. -- М.: ACT: Астрель : CORPUS, 2010. -- 303, [1] с. -- (ЭЛЕМЕНТЫ) 3. Виленкин Н.Я., В поисках бесконечности.-- М.: Наука, 1983. 160 с. 4. Горелик Г.Е., Почему пространство трехмерно? М.: Наука, 1982, 168 с. 5. Крейг У., Самое начало. Происхождение Вселенной и существование Бога, URL: <a href="http://www.otkrovenie.de/beta/xml/other/samoeNachalo.xml">http://www.otkrovenie.de/beta/xml/other/samoeNachalo.xml</a> 6. Линде А.Д., Инфляция, квантовая космология и антропный принцип. Перевод Карпова С., URL: https://arxiv.org/abs/hep-th/0211048 7. Новиков И. Д., Черные дыры и Вселенная. -- М.: Мол. гвардия, 1985. -- 190 с., ил.-- (Эврика). 8. Парадокс Гильберта, URL: <a href="http://pikabu.ru/story/paradoks_gilberta_1962200">http://pikabu.ru/story/paradoks_gilberta_1962200</a> , <a href="http://www.yaplakal.com/forum3/topic782267.html">http://www.yaplakal.com/forum3/topic782267.html</a> 9. Парадокс Гильберта, URL: <a href="http://traditio-ru.org/wiki/п¤п№яЂп№пЄпЎпЊяЃ_п"пЈп"яЊпЂпЅяЂя‚a">http://traditio-ru.org/wiki/Парадокс_Гильбертa</a> 10. Парадокс Гильберта, Википедия, URL: <a href="https://ru.wikipedia.org/wiki/пђпNoпЈяЃпЎпЊ_пNoп№яЂп№пЄпЎпЊяЃпЎпЃ">https://ru.wikipedia.org/wiki/Список_парадоксов</a> 11. Путенихин П.В. Логика противоречий. - Саратов: "АМИРИТ", 2017. - 133 с., илл., URL: <a href="https://www.elibrary.ru/item.asp?id=42733187">https://www.elibrary.ru/item.asp?id=42733187</a> <a href="https://www.twirpx.org/file/3089642/">https://www.twirpx.org/file/3089642/</a> 16.22.2017 | |
| Категория: Разное | | | |
| Просмотров: 1752 | Загрузок: 575 | |
| Всего комментариев: 0 | |