Путенихин П.В. Правила счета элементов бесконечного множества, ч.1
| [ Скачать с сервера (1.61 Mb) · Скачать удаленно (1,61 Mb) · Скриншот ] | 28.05.2021, 19:17 |
Часть 2 - URL: http://moianauka.ru/load/2-1-0-1509 Часть 3 - URL: http://moianauka.ru/load/2-1-0-1510 ЧАСТЬ 1 Аннотация Вскрыты ошибки Кантора и его последователей в логических рассуждениях о бесконечных множествах. Приведено доказательство счетности континуума, счетности всех действительных чисел. Показана ошибочность рассуждений в задаче об "Отеле Гильберта". Rules for counting elements of an infinite set. The mistakes of Cantor and his followers in logical reasoning about infinite sets are revealed. The proof of the countability of the continuum, the countability of all real numbers is given. The erroneousness of reasoning in the problem of "Hilbert's Hotel" is shown. Оглавление ЧАСТЬ 1 Связь математики и физики Равномощные множества чисел Количества натуральных чисел в группах О счетности континуума - точек на отрезке Задача об "Отеле Гильберта" ЧАСТЬ 2 Несостоявшаяся перепись Разрядность и количество чисел в массиве Счетность всех мыслимых видов чисел О равномощности отрезка и квадрата ЧАСТЬ 3 Стереографическая проекция Литература Связь математики и физики Давно замечено интересное и важное свойство математики, которая позволяет делать верные, но изначально просто как бы выдуманные описания нашего мира, предсказания: "Существует вопрос, давно волнующий людей, задумывающихся об основаниях математики: почему математика столь эффективна при описании нашего мира и столь хорошо описывает его эволюцию? ... Почему эти правила так хорошо работают?" [6] Однако вряд ли следует слишком уж сильно этому удивляться и вспоминать еще одно её такое же удивительное свойство: способность дать любой желаемый результат. Эта математика так хорошо работает просто потому, что мы и вывели её из прямых наблюдений за окружающей действительностью. Эффективно работает, значит, верно подсмотрели. Более того, в науке и, в частности, в физике уже давно замечена еще одна интересная закономерность: кажущиеся поначалу абстрактными математические выражения, уравнения вдруг оказываются описанием какого-нибудь вполне реального явления: "... физики обнаруживают, что математические построения, необходимые им для описания нового класса явления, уже исследованы математиками по причинам, не имеющим ничего общего с обсуждаемыми явлениями" [2, с.264]. Однако даже при таком явно полезном подходе следует все-таки быть предельно осторожным при формулировке выводов и следствий из этих математических построений. Можно привести ряд примеров, когда такие выкладки приводят не просто к противоречиям со здравым смыслом, но к довольно заметным противоречиям с логикой, содержат логические ошибки. Например, одним из наиболее известных таких странных выводов при исследовании бесконечных множеств элементов являются доказательства Кантора о равенстве числа точек на квадрате и линии, равной длине его ребра. Приведённые в статье выкладки опубликованы в авторской книге [11]. Равномощные множества чисел В литературе по космологии встречаются весьма любопытные рассуждения о тождественных бесконечностях. В частности делается очевидный ошибочный вывод о том, что в бесконечности часть может быть равна целому: "множество натуральных чисел (ℕ) равномощно множествам целых чисел (ℤ), чётных натуральных чисел, всех рациональных чисел (ℚ), а отрезок числовой прямой (𝕀 = [0,1], континуум) оказывается в биективном соответствии со всей числовой прямой (ℝ), а также с n-мерным евклидовым пространством (ℝn)" [1]. Несомненно, это противоречит нашей интуиции. Ведь четные числа явно составляют лишь половину всех целых чисел. Это справедливо для любой конечной совокупности чисел, но, как утверждается в цитате, не соответствует бесконечным рядам, для которых получается, что их количества равны. А утверждение в отношении отрезка буквально означает, что всем точкам отрезка соответствуют все точки всей евклидовой бесконечной плоскости. Такие же странные выводы о соотношении целого и части делаются и в космологии [7, с.77; 2, с.282]. И эти противоречащие здравому смыслу и логике выводы преподносятся в научно-популярной литературе, в книгах, в документальных фильмах (BBC) как строго доказанные факты. Ошибочность подобных методов можно показать, если произвести подсчет количеств натуральных чисел при различных способах их группирования, приводящие к любому произвольному результату. Для доказательства указанной равномощности точек отрезка и квадрата Кантор использует противоречивый, нелогичный метод. Конечно, можно предположить, что методология и доказательства Кантора и приведенные в цитате утверждения являются узкими теоретическими, частными проблемами. Однако они в явном виде использованы для того чтобы поставить под сомнение, например, одно из основных положений понятия многомерности: "... параметрическое определение размерности (по крайней мере в форме: "Размерность пространства -- это минимальное число параметров, которые необходимы, чтобы отличать точки пространства друг от друга") математически некорректно. Это стало ясно после построенного Георгом Кантором (1845--1918) знаменитого примера взаимно-однозначного соответствия между множествами точек квадрата и отрезка" [4, с.32]. Рассмотрим некоторые доказательства, которые позволят решительно отвергнуть аргументы Кантора. Количества натуральных чисел в группах Нумерация четных чисел. Например, в одном из вариантов для доказательства равномощности предлагается записать четные числа в виде бесконечного ряда, а под этим рядом написать их порядковые номера из натурального ряда чисел [7, с.78]: 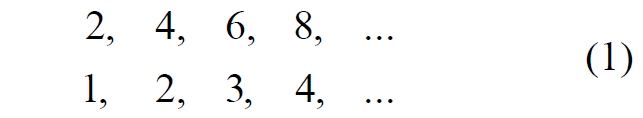 Здесь каждому четному числу соответствует один порядковый номер из натурального ряда чисел и наоборот. Значит, утверждается, число четных чисел равно числу всех чисел натурального ряда. Но это неверно. В частности, в данном примере четные числа не являются частью ряда натуральных чисел, это совершенно самостоятельный ряд, в котором вместо четных чисел могли быть любые символы. Ошибка состоит в некорректном способе подсчета, в котором часть элементов исходного ряда просто игнорируется, исключается из процедуры подсчета. Произведём подсчет другим, правильным способом. Возьмем ряд всех натуральных чисел и будем их считать самым обычным, привычным способом. Для этого каждое натуральное число будем класть в соответствующий ящик, и при этом называть его значение: один, два, три и так далее. Одновременно, по мере того, как нам будут встречаться эти числа, мы будем с каждым четным числом класть такую же цифру во второй ящик. И, для наглядности, с каждым нечётным - в третий ящик. Ну, и для ещё большей наглядности - для каждого пятого числа - в четвертый ящик. Через некоторое время посмотрим, что у нас в ящиках? Через тысячу шагов, очевидно, в первом ящике будет 1 000 чисел. Во втором и третьем - по 500, а в четвертом - только 200. Ну, или в виде соотношения 10:5:5:2. Продолжим раскладывать числа и вновь проверим содержимое ящиков теперь уже через 10 000 шагов. И в этот раз мы обнаружим, что количества чисел в ящиках соотносятся как 10:5:5:2. Нужно ли доказывать, что и через миллион, и через миллиард, и через гугл шагов количества чисел в ящиках будут соотноситься как 10:5:5:2? Если мы последовательно синхронно считаем количества чисел в натуральном ряду, то мы найдём истинное соотношение их количеств. Однако говорить, что бесконечное число всех натуральных чисел больше, чем число всех четных или нечетных чисел не совсем правильно. Эти числа образуют бесконечности, и следует говорить только об их мощности: бесконечность всех натуральных чисел в два раза мощнее, чем бесконечности всех четных или нечетных чисел и в пять раз мощнее, чем бесконечность всех чисел, кратных пяти. Утверждение, что часть может равняться целому ошибочно в самой формулировке. Мощность части бесконечности всегда меньше мощности всей бесконечности. Рассмотрим приведённый выше пример в терминах мощностей. Примем без доказательства, что количество членов множества и его мощность - это разные, но схожие по смыслу понятия. Мы не можем сравнивать число членов множеств, по определению равных бесконечности, но мы можем сравнивать их мощности. Отношение мощностей М1 и М2 равномощных множеств всегда равно конечному числу: 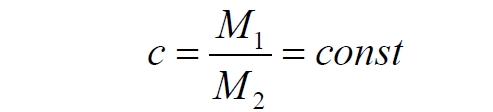 В этом случае отношение множеств (1) для четных чисел запишется в виде: 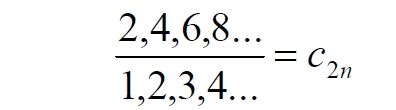 Запишем также и отношение множеств для нечетных чисел: 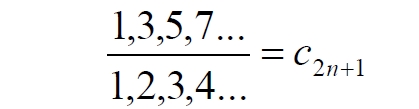 Далее нам понадобится и такое тождественное отношение: 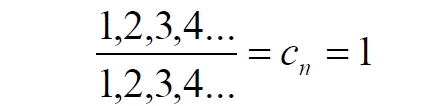 Это равенство очевидно, поскольку числитель равен знаменателю. Теперь просуммируем эти приведенные два отношения мощностей: 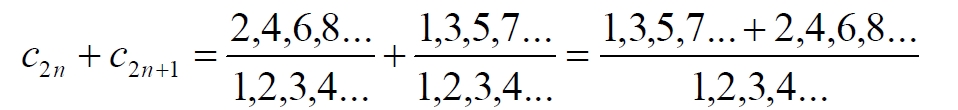 Очевидно, что последняя дробь содержит в числителе все целые натуральные числа: 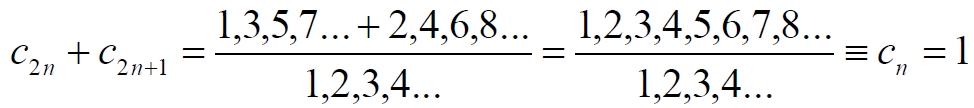 поэтому они и равны тождественно единице. Это определённо означает, что мощности множеств всех натуральных чисел и суммы множеств всех четных и нечетных чисел равны. Но это также означает и тождественное равенство их бесконечного количества членов. Очевидно, что множества четных и нечетных чисел равномощны, поэтому, разделив полученное равенство на cn, получим: 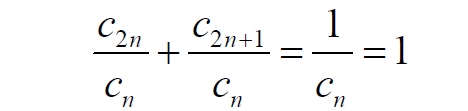 Поэтому из равенства также следует, что каждая из мощностей четных и нечётных чисел в два раза "слабее" мощности всех натуральных чисел: 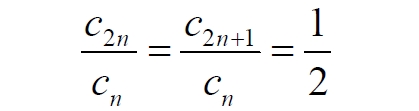 Отметим также без доказательств, что любые действия над каждым членом множества не изменяют мощности множества: 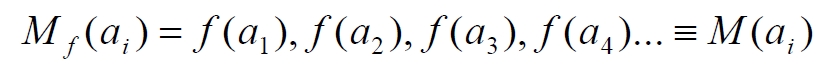 Из этого непосредственно следует, что решающее значение имеет способ, каким получено множество. Например, множество всех четных чисел может быть получено удалением из множества всех натуральных чисел нечётных или умножением на 2 каждого члена множества всех натуральных чисел: 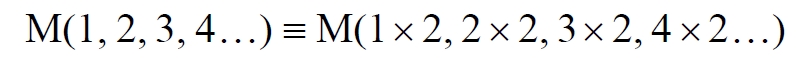 Казалось бы, последнее выражение является точной копией множества всех четных чисел М(2, 4, 6, 8...). Но это ошибочно, поскольку любые действия над всеми (или отдельными) членами множества не изменяют их полного количества и, соответственно, мощности. Поэтому справедливо (знак множества M опускаем): 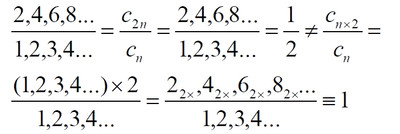 Хотя оба множества в числителях в обеих строках выглядят тождественно, на самом деле это разные множества, имеющие разную мощность. Перестановки в рядах. Еще один вариант доказательства равномощности части и целого приведен в книге [2, с.282], где предлагается вести подсчет нечетных чисел, предварительно переставив их в ряду: "В бесконечной вселенной коэффициент объема можно определить как долю, занятую областями данного типа. Но это определение приводит к неоднозначности. Чтобы проиллюстрировать природу проблемы, зададимся вопросом: какова доля нечетных чисел среди целых? Четные и нечетные числа чередуются в последовательности 1, 2, 3, 4, 5, и можно подумать, что ответом, очевидно, будет половина. Однако целые числа можно упорядочить другим способом. Например, так: 1, 2, 4, 3, 6, 8 ... Эта последовательность по-прежнему включает все целые числа, но теперь за каждым нечетным числом следует два четных, и кажется, что только треть целых чисел являются нечетными" Здесь нам отчетливо видна некорректность и противоречивость такой модификации числового ряда, которая строго последовательно и логично легко доводится до абсурда. Для этого все нечетные числа поместим в самый конец бесконечной последовательности. Теперь при поверхностном анализе последовательности мы обнаружим, что в ней нечетных чисел нет вообще. Конечно, мы догадываемся, что все они где-то дальше, но, как бы долго мы ни просматривали последовательность, мы никогда не встретим в ней ни одного нечетного числа. Однако итог явно абсурден: нечетные числа точно есть, но мы их почему-то не пересчитываем. Причина заключается просто в выборе метода подсчета: игнорирование длины ряда. Мы же сами каким-то образом перенесли нечетные числа в конец ряда? Ну, так и нумеровать тогда следует весь ряд. Это же относится и к предложенному выше методу упорядочивания. Каким-то образом эти числа перетасованы? Вплоть до последнего. Ну, так и считать следует соответственно - до последнего числа. Если же числа перетасовываются в процессе счета, тогда "временно вынутые из ряда нечетные числа" все время будут где-то скапливаться. Трудно будет не заметить это бесконечно большое хранилище нечетных чисел. С другой стороны, мы можем проделать то же самое и с четными числами, например, получив в результате, что их в общем ряду только треть. Иначе говоря, один и тот же метод показывает, что среди целых чисел нечетных одновременно только половина и только две трети. Понятно, что методика, дающая два взаимоисключающих результата не вызывает доверия. Группировка степеней. Такие методики пересчета, отождествления всегда содержат плохо скрытую подмену понятий. Например, с рядом натуральных чисел отождествляется ряд степеней 101, 102, 103 ... 10n... и так далее. Таким же образом устанавливается взаимно однозначное соответствие и между множеством натуральных чисел и множеством всех квадратов натуральных чисел 12, 22, 32, ... n2... и так далее. Но принять такое отождествление нет никаких оснований. Нужно просто обратить внимание на то, что же именно отождествляется. В обоих приведенных примера сразу же можно заметить присутствие члена натурального ряда. Понятно, что отождествляются не значения членов ряда, а их порядковые номера, которые самым наглядным образом обозначены в каждом из членов рядов. До начала отождествления каждый член ряда уже имеет свой натуральный порядковый номер, а значение самого члена ряда не имеет никакого смысла. Это могут быть и летучие обезьяны с соответствующей биркой на шее, и протоны в бесконечной Вселенной, которые ещё только предстоит пометить соответствующим номером, и даже множество миров Эверетта. Группировка в пары. Попробуем теперь просто пересчитать, перенумеровать все натуральные числа, предварительно соединив их в пары четное-нечетное число: (1,2), (3,4), (5,6), то есть, присваивая каждой паре последовательно номера 1, 2, 3, 4 и так далее. Очевидно, что каждой паре будет присвоен один номер, натуральное число. И мы получаем явное противоречие, поскольку это означает, что количество всех натуральных чисел, собранных в пары, в два раза больше количества всех натуральных чисел. Буквально, количество всех натуральных чисел в два раза больше количества всех натуральных чисел. Но натуральные числа можно группировать и тройками, пятерками, десятками и так далее. Десять рядов. Еще более наглядно подмена понятий будет видна, если составить из натурального ряда десять новых рядов, каждый из которых содержит натуральные числа, оканчивающиеся на 0, 1, 2 и так далее до 9. Если теперь пересчитать их количества, то для каждого ряда, как и в случае (1) мы получим количество, совпадающее с количеством натуральных чисел. Теперь вновь соединим все эти ряды в единый. Очевидно, что в результате мы получим исходный ряд - натуральные числа. Получается, что количество членов просуммированного ряда в десять раз больше, чем в ряду натуральных чисел. Но ведь просуммированный ряд - это тот же самый натуральный ряд. Здесь совершается та же ошибка: подсчет без учета принадлежности чисел выделенных рядов исходному, натуральному ряду. Квадратная таблица. Однако и это не предел. Можно, например, составить таблицу из n строк натуральных чисел, поэтому, соответственно, столбцов будет тоже n, где n - натуральное число. Теперь подсчитаем, перенумеруем диагональным процессом Кантора все числа этой таблицы. Очевидно, что каждое из чисел получит свой порядковый номер, которых, понятно, будет ровно n, стремящееся к бесконечности. Но таблица определенно содержит n2 элементов. Получается, что количество n2 элементов равно n, или, другими словами, количество всех натуральных чисел равно квадрату количества всех натуральных чисел. Конечно, сами натуральные числа к этому непричастны. Проблему создаёт выбор специфических способов подсчета, в основе которых явно лежат методы Кантора, позволяющие получить любой, произвольный результат. Поскольку один и тот же метод при корректном применении даёт разные результаты, такой метод не может быть верным. О счетности континуума - точек на отрезке Как утверждается со ссылкой на методологию счета Кантора, множество всех действительных чисел несчетно, то есть, невозможно их пересчитать, присвоив каждому из них некоторое натуральное число - номер, поскольку всегда останутся непронумерованные числа [3, с.73-74]. Вообще-то, на первый взгляд, интуитивно это выглядит вполне очевидно. Рассмотрим, например, следующую явно бесконечную последовательность действительных чисел: 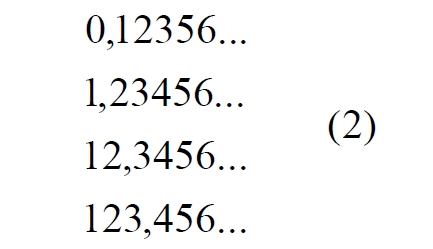 В этих числах запятая просто занимает позицию n, представляющую натуральное число, поэтому чисел в указанной последовательности в точности равно числу строк, n, где n равно бесконечности. Поскольку все номера натуральных чисел использованы для нумерации этих действительных чисел, то очевидно, что остальное множество действительных чисел осталось без номеров, то есть их множество - несчетно. В связи с хитростями нумерации, как правило, вспоминают математика Кантора, который, как считается, доказал, что число точек на отрезке прямой сосчитать никаким способом нельзя. Утверждается, что их нельзя перенумеровать с помощью бесконечного ряда натуральных чисел, приписывая каждой точке свой номер, в каком бы порядке мы ни выбирали эти точки. Всегда останется хотя бы одна точка, на которую не хватит номера! Перенумеровать или, тождественно, пересчитать бесконечное количество чего-либо, в том числе, сосчитать точки отрезка, действительно, невозможно физически. Однако приводимое затем доказательство, как правило, начинается со слов: "Представим, что вопреки нашему утверждению кому-то удалось перенумеровать точки этого отрезка", после чего приводятся хитрые комбинации с нумерацией. Но здесь следует напомнить фундаментальный принцип классической логики и классической математики, который постулирует полное отрицание актуальной бесконечности: "Infinitum Actu Non Datur" (Аристотель) - "актуальная бесконечность не существует". Принцип утверждает потенциальный, т.е. принципиально незавершаемый характер бесконечности множества. Актуальная, то есть, пересчитанная бесконечность лишена смысла. Бесконечностью может считаться лишь потенциальная бесконечность, завершить счет членов которой невозможно. Поэтому приводимое доказательство на этих словах можно и прервать - оно некорректно с самого начала. Впрочем, в этом вопросе особое мнение, которое следует признать некорректным, приписывается Давиду Гильберту. По мнению немецкого математика, одного из величайших умов своего времени, главное различие между актуальной и потенциальной бесконечностью заключается в следующем. Потенциально бесконечное есть всегда нечто возрастающее и имеющее пределом бесконечность, тогда как актуальная бесконечность - это завершённое целое, в действительности содержащее бесконечное число предметов [5]. В литературе можно встретить описание довольно интересного способа подсчета количества точек на отрезке линии. Нетрудно догадаться, что в этом примере использованная методика счета ошибочна и ведет к ошибочному выводу. Несложное доказательство несчетности содержит не очень сильно скрытую подмену понятий. Итак: "Теперь уже несложно доказать, что множество всех точек на прямой линии несчетно. Вместо этого множества можно говорить о множестве всех действительных чисел, так как каждой точке прямой соответствует действительное число и обратно. Каждое действительное число можно записать в виде бесконечной десятичной дроби вида α, α1 α2 α3 ... αn ..." [3, с.73-74]. Как видим, ряд знаков имеет бесконечное счетное количество знаков и, резонно предположим, что так же считает и автор доказательства. Сразу же заметим, что утверждения следует признать абсурдными. Любое конечное число всегда меньше бесконечности. "Предположим, что нам удалось каким-то образом перенумеровать все действительные числа. Чтобы доказать, что это предположение неверно, достаточно построить хоть одно незанумерованное число. ... поступим следующим образом. Сначала напишем нуль и поставим после него запятую. Потом возьмем число, получившее первый номер, и посмотрим на его первый десятичный знак после запятой (то есть на число десятых)" [там же]. Для определенности отметим, что поиск незанумерованного числа производится, как можно заметить, на отдельном интервале всех действительных чисел [0, 1]. Сначала как на неточность в этом рассуждении, как и в предыдущем доказательстве, сразу же укажем на очевидное, но, похоже, незамеченное обстоятельство: на самом деле при последовательном, возрастающем счёте у второго числа вторая цифра тоже будет 0. И у третьего. И у четвертого. И у числа, занимающего бесконечно большую позицию. На словах это, возможно, не совсем ясно, поэтому покажем это на "виновнике торжества" - на оцифрованном отрезке: 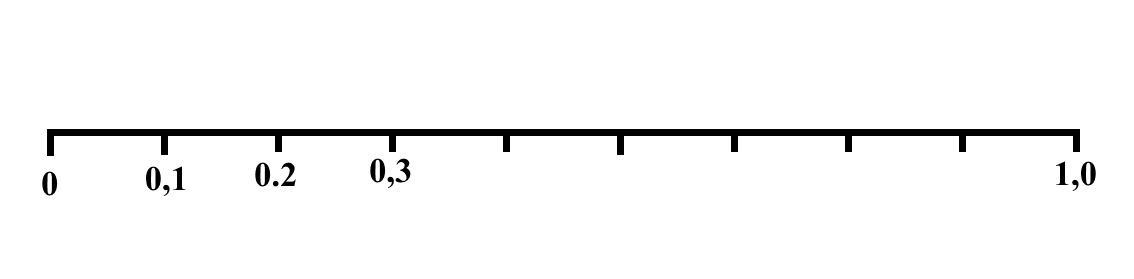 Рис.1. Оцифрованный отрезок, отдельный интервал всех действительных чисел На рисунке видно, что первая цифра после нуля будет отличной от нуля, единица будет только после точки 0,1 отрезка. На интервале от 0 до 0,1 содержится счетное (пока оспариваемое) количество точек. Во всяком случае, это не одна, не миллион и даже не гугл точек, равный 10100, а в бесконечное число раз больше. У всех этих чисел первой цифрой после запятой будет ноль. Следовательно, искомое число пока находится вблизи нулевой точки, в самом начале отрезка [0, 1]. "Если эта цифра отлична от 1, то в числе, которое мы пишем, поставим после запятой 1, а если эта цифра равна 1, то поставим после запятой 2" [3, с.73-74]. Еще раз отметим, что отличная от единицы цифра в первой позиции после нуля первого числа будет нулем. Следовательно, в "искомом" числе после запятой первой будет 2. То есть, число будет 0,2. Сразу же на рисунке находим, что эта точка на отрезке есть - это точка 0,2. "Затем перейдем к числу, получившему второй номер, и посмотрим на его вторую цифру после запятой. Снова если эта цифра отлична от единицы, то в числе, которое мы пишем, поставим на месте сотых цифру 1, если же эта цифра является единицей, то поставим цифру 2" [там же]. Как и в предыдущем случае, вторым знаком опять будет ноль, поскольку точки расположены рядом и их номера различаются лишь в очень далекой позиции после нуля. Следовательно, и вторая цифра искомого числа будет 2. То есть, это будет число 0,22. По рисунку видно, что и эта точка на отрезке имеется. Она находится правее точки 0,2 и отстоит от неё примерно на 1/5 отрезка от 0,2 до 0,3. "Точно так же будем действовать и дальше, каждый раз обращая внимание лишь на n-ю цифру числа, получившего n-й номер. В результате мы выпишем некоторое число, например, N=0,1121211. . . [там же]. Но мы уже можем заметить, что такое число не получается. А получится число 0,22222..., в котором цифра 1 появится очень и очень не скоро. И эта цифра, единица также будет тиражироваться многократно. В конечном счете, формируемое число примет вид: N=0,22222...11111...22222...11111 Кстати, можно догадаться по алгоритму, что число будет в основном состоять из двоек, поскольку из 10 цифр единица, которую помечаем двойкой, только одна. "Ясно, что это число не получило никакого номера: в первом десятичном знаке оно отличается от числа с номером 1, во втором -- от числа с номером 2, . . ., в n-м -- от числа с номером n и т. д." [3, с.73-74]. Верно это только отчасти, поскольку в целом неверно. Указанные совпадения, действительно, на первом участке отрезка отсутствуют. Однако это найденное число совпадает в первом знаке с бесконечным множеством чисел, соответствующих другой точке отрезка - [0.2, 0.3]. Первым и вторым знаками оно соответствует множеству чисел следующих точек этого отрезка. Первым, вторым и третьим - следующему множеству точек отрезка. И так далее - до бесконечности! Проще говоря, "найденное" число будет находиться правее числа 0,222 и бесконечно близко к нему, никогда не достигая числа 0,223. "Чтобы читателю стало яснее, как выписывается число, не получившее номера, предположим, что при выбранной нумерации первые пять чисел имеют следующий вид: 4,27364... --1,31226... 7,95471... 0,62419... 8,56280... " [там же]. Здесь очевидна небольшая неточность, поскольку автором, судя по всему, выбран интервал [0, 1], а на этом интервале таких чисел при выбранной нумерации не будет никогда. Однако эту неточность оставим без критики, просто заменив в них цифру перед запятой на ноль, поскольку пояснение вполне верно описывает принцип формирования искомого числа. "Тогда число, не получившее номера, будет начинаться со следующих десятичных знаков: 0,12121 . . . Разумеется, не только это, но и многие другие числа не получили номеров (мы могли бы заменять все цифры, кроме 2, на 2, а цифру 2 на 7 или выбрать еще какое-нибудь правило). Но нам достаточно существования одного-единственного числа, не получившего номера, чтобы опровергнуть гипотезу о возможности нумерации всех действительных чисел" [3, с.73-74]. Еще раз отметим, что доказательство на самом деле рассматривает бесконечно малую часть всех действительных чисел - на интервале [0, 1]. Предложенный способ просмотра чисел некорректен. При таком способе все просматриваемые действительные числа на этом интервале будут сгруппированы возле нулевой точки. И ожидаемого числа 0,12121, приведенного в качестве примера, получено не будет никогда. А будет образовано указанное выше число N из бесконечного количества двоек. Следовательно, в этом отношении доказательство не может достичь успеха, поскольку полученное число точно имеется на близлежащем интервале. Действительно, на интервале, например, от 0,222 до 0,223 присутствуют все возможные комбинации знаков после запятой, в том числе и знаков указанного числа N. Конечно, в доказательстве явно не указана последовательность номеров чисел. Но под "нам удалось" тоже явно никто не указан. Эти самые "нам" могли перенумеровать числа интервала подряд: сначала все возле нуля, затем они дошли до 0,1 и так далее. В рассмотренном выше примере с перестановкой запятой (2) такие пропущенные числа очевидны, например, в нем отсутствуют числа 1,111 и 2,222. Однако и традиционный метод нахождения пропущенного числа изначально содержит логическую ошибку, противоречие. Подбор такого числа дает результат, который изначально обязательно должен был быть подсчитанным, пронумерованным натуральным числом. Покажем эту очевидную логическую ошибку такого нахождения отсутствующего числа в более явном виде. Предположим, что в процессе поиска получено новое число, скажем, 0,7182814159.... Однако это число не является новым, отсутствующим в пронумерованном множестве. Это странным образом не замеченное очевидное обстоятельство. Очевидно, что последовательности цифр после запятой всех действительных чисел являются полными, исчерпывающими, содержащими все без исключения их возможные комбинации. То есть, любая наперед заданная комбинация цифр, в том числе и у этого "найденного", обязательно присутствует в бесконечном множестве действительных чисел. Более того, любое число с конечным числом знаков как фрагмент, шаблон присутствует в этом ряду бесконечное число раз. Действительно, "найденных" чисел вида 0,718nnn... - бесконечное множество, как и чисел 0,7182814nnn..., где n - любая цифра, поэтому среди них обязательно имеется и "найденное". Следовательно, любое найденное подобным образом число, обязательно имеется среди подсчитанных, то есть, оно пронумеровано, как и любое другое из множества действительных чисел, что означает счетность всех действительных чисел. Ошибочность доказательств многих тезисов Кантора вызвана выбором специфического метода подсчета числа элементов, неудачного способа записи последовательностей этих элементов, в результате чего отождествление элементов оказалось завуалированным. Очевидно, что указанный метод доказательства несчетности множества действительных чисел, который можно назвать традиционным, содержит явную логическую ошибку и непригоден сам по себе. Этот метод опирается на недопустимое предположение "если кому-то удалось все их пересчитать, то можно найти пропущенное". Вместе с тем существует достаточно очевидный способ записи элементов континуума, наглядно доказывающий счетность всех мыслимых видов чисел, и позволяющий записать все их строго последовательно. Покажем это на примере способа записи всех действительные числа, меньших нуля. Способ записи достаточно очевиден: нужно просто записывать после запятой все последовательные натуральные числа в обратном порядке, инверсно "задом наперед". Например, под номером 12345678 будет записано действительное число 0,87654321, а инверсией последовательных натуральных чисел 996, 997, 998, 999, 1000 будет создан фрагмент последовательности действительных чисел: 0,699?0,799?0,899?0,999?0,0001 и так далее. Такая инверсная запись дробной части чисел, меньших единицы, позволяет записать всю их непрерывную, бесконечную последовательность. Инверсная запись, "задом наперед" используется для того, чтобы при возрастании номера сохранялись значащие нули, поскольку при обычной записи будут пропущены, например, действительные числа, имеющие нули сразу после запятой. Очевидно, что бесконечная последовательность содержит все без исключения действительные числа, меньшие нуля, в частности, полную дробную часть чисел π (3,14159...), числа Эйлера - е (2,71828...), основания натуральных логарифмов, константу пропорциональности Ландау - Рамануджана С (0,76422...) и постоянную тонкой структуры α ≈ 1/137, причем с бесконечной точностью. Для удобства эти дробные числа с нулевой целой частью можно представить, например, записью следующего вида: 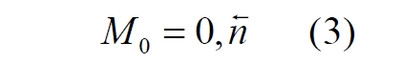 где индекс 0 означает, что все числа этого множества не превышают единицы, то есть, перед запятой у них записан 0, а n со стрелкой влево над ним - это обычное натуральное число, записанное после запятой в обратном порядке, "задом наперед", как дробная часть этого элемента множества. Очевидно, это число n является порядковым номером соответствующего элемента множества M0, точки линии. Теперь возьмем отрезок, линию [0,1] и отождествим каждую точку этой линии с полученной числовой последовательностью (3). Очевидно, что каждая точка отрезка будет единственно отождествлена с единственным числом последовательности, парно. Ни одна точка или число не будут пропущены. Какое бы число мы ни взяли, на линии обязательно будет точка с таким же значением. Наоборот, какую бы мы не взяли точку на линии, этот номер обязательно будет в созданном массиве. Иначе говоря, рассмотренный отрезок числовой прямой [0, 1], континуум оказывается в биективном соответствии со всеми числами созданного множества. Собственно процесс нумерации элементов массива или точек линии также достаточно очевиден. В этом процессе, как можно обнаружить, точки, элементы линии, числа сформированного ряда, матрицы оказываются расположенными не в виде монотонной последовательности, а "вперемешку". 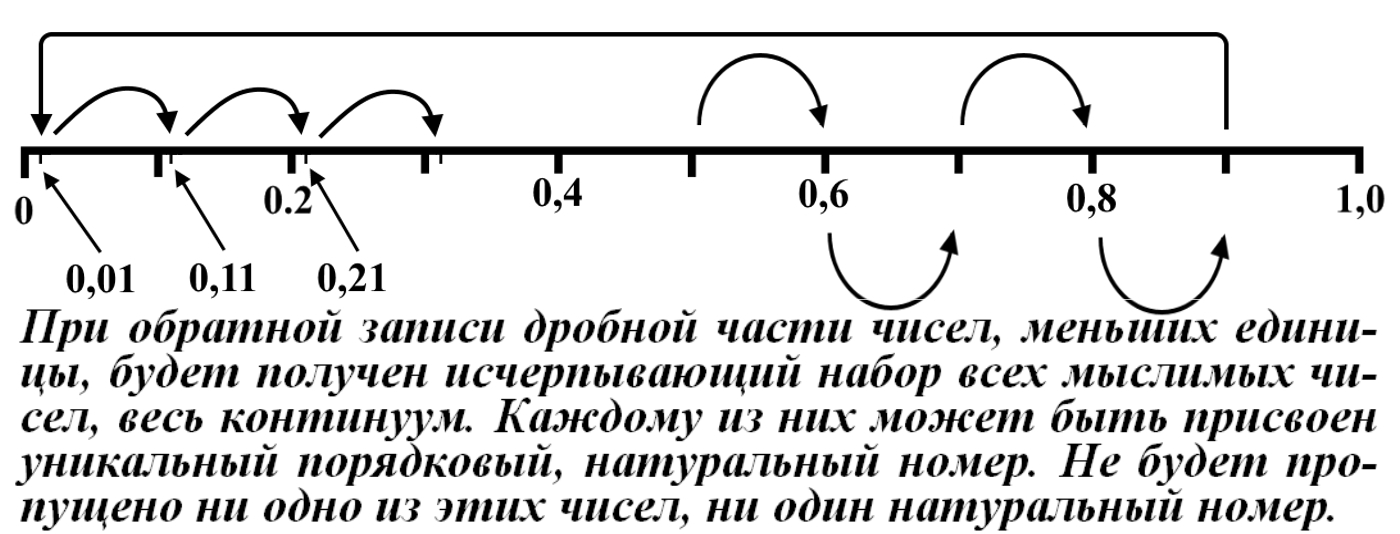 Рис.2. Нумерация точек отрезка На рисунке показан фрагмент последовательной нумерации точек, начиная с точки 0,5 и заканчивая на точке 0,31. Мы последовательно рассматриваем фрагмент, точки с натуральными порядковыми номерами 5, 6, 7, 8, 9, 10, 11, 12, 13, по которым из выражения (3) определяем значения этих точек: 0,5 (точка номер 5); 0,6 (точка номер 6); 0,7 (точка номер 7 и так далее); 0,8; 0,9; 0,01 (точка номер 10); 0,11; 0,21; 0,31 (точка номер 13). Как видим, порядковые номера точек равномерно возрастают, но сами точки при этом "скачут" по линии. Отметим главное: фактическое значение точки "возникает" в самом процессе нумерации. То есть, сначала мы выбираем некоторый или очередной, натуральный порядковый номер точки, а затем определяем её местоположение на линии и присваиваем этой точке выбранный номер. Собственно говоря, нумерация элементов массива и означает присвоение конкретному элементу некоторого определенного номера, как бы навешивание на элемент таблички с номером. Поэтому выбрав элемент, мы можем увидеть его номер, а выбрав номер, узнать, какому элементу он принадлежит. В рассмотренном случае с нумерацией точек линии натуральный порядковый номер, например, 12 389 принадлежит точке на линии со значением 0,98321. Наоборот, точка линии со значением, например, 0,5612999 имеет в массиве порядковый номер 9 992 165. Такой же алгоритм можно использовать и для нумерации точек плоских или объемных, многомерных объектов, например, точек куба. В случае многомерных объектов номер преобразуется к виду (3) по методу Кантора, созданного им для отождествления точек линии и квадрата [3, с.77]. Предположим, некая точка куба имеет следующие координаты, в которых буквы α, β и γ обозначают любую цифру в этих числах: 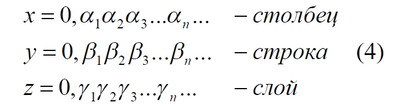 Используя метод Кантора, формируем из этих чисел новое число: 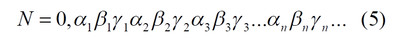 Отсутствующие цифры для какого-либо индекса заменяем нулями. Дробную часть полученного комбинированного числа инвертируем, поворачиваем "задом наперед", согласно (3), и получаем натуральный порядковый номер рассмотренной точки куба. Например, точка куба с координатами p(x, y, z) = (0,123; 0,321; 0,9171) при комбинировании даст число N=139 221 317 001, что означает порядковый номер точки в бесконечном их массиве, равный 100 713 122 931. Понятно, что обратным преобразованием можно так же найти координаты любой точки по её номеру. Например, точка с порядковым номером 1 234 567 890 имеет в кубе координаты p(0,0741; 0,963; 0,852). Рассмотренный вариант относится к кубу с единичным ребром, но он может быть легко расширен на куб с любым размером ребра, а также на объекты вообще с любым числом измерений. Наконец, метод позволяет перенумеровать и составные элементы: комплексные числа, кватернионы и тому подобные. Например, комплексное число можно представить в виде 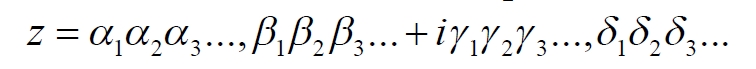 В этой записи буквами α и γ обозначены целая часть числа реальной и мнимой части, а буквами β и δ, соответственно, их дробные части. Например: 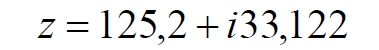 Количество цифр α, β, γ и δ в записях может быть любым. Теперь, используя метод комбинации, можно получить число N, инверсная запись которого и будет обозначать натуральный порядковый номер этого числа в их бесконечном массиве. Например, приведенное выше комплексное число будет иметь в бесконечном массиве всех возможных комплексных чисел натуральный порядковый номер 200 123 021 325. Кстати, можно заметить, что в таком массиве первые 10 чисел (0...9) являются реальными, а число i (комплексная единица) находится на позиции 100 и имеет порядковый номер 10. Также заметим, что при таком подходе основой всех чисел являются вещественные числа, а различные комплексные и им подобные - это простая комбинация этих базовых чисел. Условно говоря - все эти комбинационные числа являются своеобразной тенью, миражом чисел реальных. Нетрудно заметить, что нумерация комплексных чисел тождественна нумерации точек квадрата. В этих частных случаях можно легко применить для их нумерации традиционный диагональный процесс Кантора. Далее, если составить множество строк, подобных выражению (3), в каждой из которых вместо нуля теперь уже будут записываться последовательные натуральные числа, то образуется квадратная таблица, матрица, содержащая все без исключения положительные действительные числа. То есть, запись (3) будет иметь следующую расширенную форму: 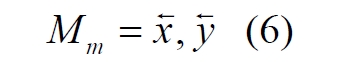 где x, y - это обычные натуральные числа, которые, как и выше, записаны в обратном порядке, "задом наперед", что обозначено обратными стрелками над ними. Нетрудно догадаться, что эти числа могут обозначать соответствующие координаты точек квадрата. Дублирование строк со знаком минус добавит в таблицу и все отрицательные действительные числа. Если теперь записать матрицу координат его точек по выражению (5) для их подсчета диагональным процессом Кантора [3, с.70], то полученная запись будет иметь вид: 0,0→0,1→0,2→0,3→0,4→... →0,0001 и так далее. 1,0→1,1→1,2→1,3→1,4→... →1,0001 и так далее. 2,0→2,1→2,2→2,3→2,4→... →2,0001 и так далее. 3,0→3,1→3,2→3,3→3,4→... →3,0001 и так далее. ... 10,0→10,1→10,2→10,3→10,4→... →10,0001 и так далее. Нетрудно заметить, что такая запись содержит весь бесконечный ряд действительных чисел, причем слева (столбцом) и справа от запятой записаны независимые ряды в диапазонах значений от 0 до 1. Понятно, что ряд слева от запятой нужно читать справа налево, добавив в начале него 0 и запятую. Такая трактовка этих последовательных числовых рядов позволяет присвоить значения их членов координатам точек квадрата, присвоить каждую пару этих чисел x, y каждой из точек квадрата со стороной 1 - без взаимных пропусков, то есть, обеспечить их полное биективное соответствие. Действительно, каждая точка квадрата на его некоторой, например, горизонтальной линии может быть пронумерована, как и точки линии, дробной частью x чисел представленного квадратного массива. Соответственно, каждой линии по вертикали так же может быть присвоен номер y, записанный инверсно, "задом наперед", то есть, и всё бесконечное множество горизонтальных линий квадрата будет пронумеровано всем рядом действительных чисел, меньших единицы. Теперь все точки квадрата в созданной матрице можно пересчитать диагональным процессом Кантора. Причем, отчетливо видно, что в представленной матрице первая строка номеров точек квадрата тождественна строке номеров точек линии (3) при y = 0. А это означает, что количество точек на линии в бесконечное число раз меньше количества точек на квадрате. Следует признать, что нумерация точек квадрата диагональным процессом менее удобна, чем способ конвертации номеров (6). При конвертации мы легко можем по натуральному порядковому номеру N точки p(x,y) определить её координаты x, y и наоборот. Использование же в этих целях выражения (5) связано с заметными вычислительными трудностями. Таким образом, приведенные рассуждения позволяют подвести итог и сделать однозначный вывод: Вся бесконечная последовательность действительных чисел, континуум любого числа измерений являются счётными, все они могут быть пронумерованы натуральными числами. Задача об "Отеле Гильберта" Судя по всему, вопросы бесконечных множеств сложны не только для рядовых математиков. Иной раз в слабом их понимании можно заподозрить и величайших специалистов в этой области. Рассмотрим рассказ, который, как считается, предложил Гильберт где-то в третьем десятилетии 20 века [9, 8, 10; 3, с.70-71]. Представим себе гостиницу с бесконечным числом комнат. Комнаты пронумерованы натуральными числами от 1 до ∞. Однажды в гостиницу вошел человек и попросил снять комнату. К сожалению, для нового гостя не нашлось комнаты, так как отель был полностью заполнен бесконечным числом гостей, и не было ни одного свободного номера. Как предоставить новому гостю свободную комнату, не выселяя никого из постояльцев? Несмотря на то, что по условиям задачи все номера заняты, утверждается, что, тем не менее, существует возможность выделить сколько угодно свободных комнат. Для этого необходимо переселить постояльца из первой комнату во вторую, постояльца из второй комнаты в третью и так далее. То есть, каждого постояльца из комнаты с номером n необходимо переселить в комнату с номером n+1, n→n+1. В результате этого освобождается комната с номером один, и в неё можно поселить нового гостя. Здесь неявно подразумевается, что переселение выселением не является. Но это решение ошибочно. По условиям задачи определённо сказано, что свободных номеров нет! Следовательно, данный "парадокс" Гильберта является псевдо парадоксом [9], поскольку вместо подселения производится выселение. В предложенном решении производится подмена понятий. Состояние, стационарное, неизменное - заполненность всех номеров жильцами - подменяется процессом, динамическим, движением - переселением постояльцев из одного номера в другой. Во-первых, этот процесс будет длиться вечно, во-вторых, в случае даже одного нового гостя, на всём протяжении процесса переселений один из постояльцев всегда будет без гостиничного номера, то есть, будет сидеть в коридоре, что является нарушением условий решения задачи. Иначе говоря, все постояльцы просто поделились своим временем проживания с новым жильцом как в пословице "с миру - по нитке". Собственно математическая ошибка состоит в том, что за большим числом постояльцев как-то незаметно прячется суть задачи. Математической процедурой, манипуляцией с бесконечностями подменяется само содержание исходного тезиса: подселение в заполненный отель дополнительных постояльцев. Показать эту подмену можно, если взять противоположный предельный вариант: в отеле всего один номер, и он занят. Для того чтобы поселить нового, прежнего постояльца временно выселяют буквально в коридор под предлогом переселения. Здесь, как видим, и обнаруживается скрытая подмена понятий переселения и выселения. Вновь пришедшего гостя селят в освободившийся номер. Но прежнего постояльца тоже надо куда-то поместить. Поэтому вновь заселенного гостя опять выселяют, а на его место селят прежнего постояльца. И так по кругу. В конечном счете, каждый из них в номере проживает только половину времени, а вторую - на стуле в коридоре. В таком варианте задача принципиально ничем не отличается от задачи с бесконечным числом комнат. Добавим ещё одну комнату и будем по кругу переселять теперь уже троих постояльцев. Можно добавить и четверную комнату и производить всё ту же процедуру "переселения-выселения". Дойдя до бесконечности, мы и получим парадокс отеля в исходном варианте. Однако в его минимальной конфигурации мы явно обнаруживаем: постояльцы, по сути, часть времени проводят на стуле возле комнаты. При бесконечном числе комнат и конечном числе новых постояльцев это время стремится к нулю. Отличие только в этом. Если же число постояльцев растет, как предлагается в расширенных версиях парадокса, то и время "на стуле около комнаты" также будет расти вплоть до той же исходной величины - половины времени проживания. Рассмотренные решения "парадоксов" нарушают главный принцип отелей: постоялец должен вселиться и жить в нем, пока сам не решит его покинуть. Вместе с тем, обнаруженное нарушение можно отнести к слабому опровержению решения задачи. Более важным выводом из неё является заявленное доказательство несчетности всех действительных чисел. Но ошибочно и это доказательство. Литература 1. Бесконечность, Википедия, URL: <a href="https://ru.wikipedia.org/wiki/п"пЅяЃпЊпЎпҐпЅя‡пҐпЎяЃя‚яЊ">https://ru.wikipedia.org/wiki/Бесконечность</a> 2. Виленкин А., Мир многих миров: Физики в поисках параллельных вселенных Алекс Виленкин, пер. с англ. А. Сергеева. -- М.: ACT: Астрель : CORPUS, 2010. -- 303, [1] с. -- (ЭЛЕМЕНТЫ) 3. Виленкин Н.Я., В поисках бесконечности.-- М.: Наука, 1983. 160 с. 4. Горелик Г.Е., Почему пространство трехмерно? М.: Наука, 1982, 168 с. 5. Крейг У., Самое начало. Происхождение Вселенной и существование Бога, URL: <a href="http://www.otkrovenie.de/beta/xml/other/samoeNachalo.xml">http://www.otkrovenie.de/beta/xml/other/samoeNachalo.xml</a> 6. Линде А.Д., Инфляция, квантовая космология и антропный принцип. Перевод Карпова С., URL: https://arxiv.org/abs/hep-th/0211048 7. Новиков И. Д., Черные дыры и Вселенная. -- М.: Мол. гвардия, 1985. -- 190 с., ил.-- (Эврика). 8. Парадокс Гильберта, URL: <a href="http://pikabu.ru/story/paradoks_gilberta_1962200">http://pikabu.ru/story/paradoks_gilberta_1962200</a> , <a href="http://www.yaplakal.com/forum3/topic782267.html">http://www.yaplakal.com/forum3/topic782267.html</a> 9. Парадокс Гильберта, URL: <a href="http://traditio-ru.org/wiki/п¤п№яЂп№пЄпЎпЊяЃ_п"пЈп"яЊпЂпЅяЂя‚a">http://traditio-ru.org/wiki/Парадокс_Гильбертa</a> 10. Парадокс Гильберта, Википедия, URL: <a href="https://ru.wikipedia.org/wiki/пђпNoпЈяЃпЎпЊ_пNoп№яЂп№пЄпЎпЊяЃпЎпЃ">https://ru.wikipedia.org/wiki/Список_парадоксов</a> 11. Путенихин П.В. Логика противоречий. - Саратов: "АМИРИТ", 2017. - 133 с., илл., URL: <a href="https://www.elibrary.ru/item.asp?id=42733187">https://www.elibrary.ru/item.asp?id=42733187</a> <a href="https://www.twirpx.org/file/3089642/">https://www.twirpx.org/file/3089642/</a> 16.22.2017 | |
| Категория: Разное | | | |
| Просмотров: 1772 | Загрузок: 598 | |
| Всего комментариев: 0 | |