Путенихин П.В. Диаграммы Пенроуза – что это такое? Часть 2.
| [ Скачать с сервера (1.72 Mb) · Скачать удаленно (1,72 Mб) · Скриншот ] | 05.06.2021, 14:58 |
ЧАСТЬ 2 Часть 1. URL: http://moianauka.ru/load/2-1-0-1521 Часть 2. URL: http://moianauka.ru/load/2-1-0-1522 Аннотация Диаграммы Пенроуза в исходном варианте являются системой координат, не имеющей принципиальных отличий, например, от традиционной декартовой системы координат. Использованное в диаграммах Пенроуза конформное тангенциальное сжатие также имеет принципиальное сходство, например, с логарифмическим сжатием декартовых координат. Однако некоторые модификации диаграмм Пенроуза приводят к возникновению на них физически противоречивых областей, например, с анизотропией времени, разрывами пространства, деформацией координатной сетки. Penrose diagrams - what are they? The Penrose diagrams in the original version are a coordinate system that has no fundamental differences, for example, from the traditional Cartesian coordinate system. The conformal tangential compression used in the Penrose diagrams also has a fundamental similarity, for example, with logarithmic compression of the Cartesian coordinates. However, some modifications of the Penrose diagrams lead to the appearance of physically contradictory regions on them, for example, with anisotropy of time, ruptures of space, deformation of the coordinate grid. Оглавление Диаграмма как система координат Классы диаграмм Пенроуза Диаграмма в форме ромба (квадрата) 2М-диаграмма Пенроуза Алгоритм построения диаграммы Пенроуза Динамические диаграммы Пенроуза Динамическая диаграмма обмена световыми сигналами Произвольные фигуры на диаграмме Заключение Литература Произвольные фигуры на диаграмме Как отмечено, диаграммы Пенроуза принципиально ничем не отличаются от традиционных, классических декартовых систем координат. Поэтому их можно использовать таким же образом для любых графических построений. Поскольку координатная сетка на диаграммах Пенроуза криволинейная, такие фигуры и графики выглядят довольно-таки экзотически - рис.11. Координатная сетка, линии погашены. Например, отрезок синусоиды t = sin(r) примерно в 10-12 периодов выглядит как сигнал, амплитуда которого сначала возрастает, затем убывает, а частота, наоборот, сначала уменьшается, затем возрастает. При этом форма синуса непривычно искривлена. Более привычный вид имеет гипербола t = 1/x. Два отрезка ветвей гиперболы в первом и третьем квадрантах отчетливо напоминают дуги окружности, но это гиперболы. Еще более непривычный вид имеет отрезок параболы t = x2. На довольно незначительном интервале изменения аргумента парабола имеет каплевидную или линзообразную форму. Понятно, что на диаграмме можно изобразить все эти графики функций полностью - в диапазонах изменения аргумента и функции от минус до плюс 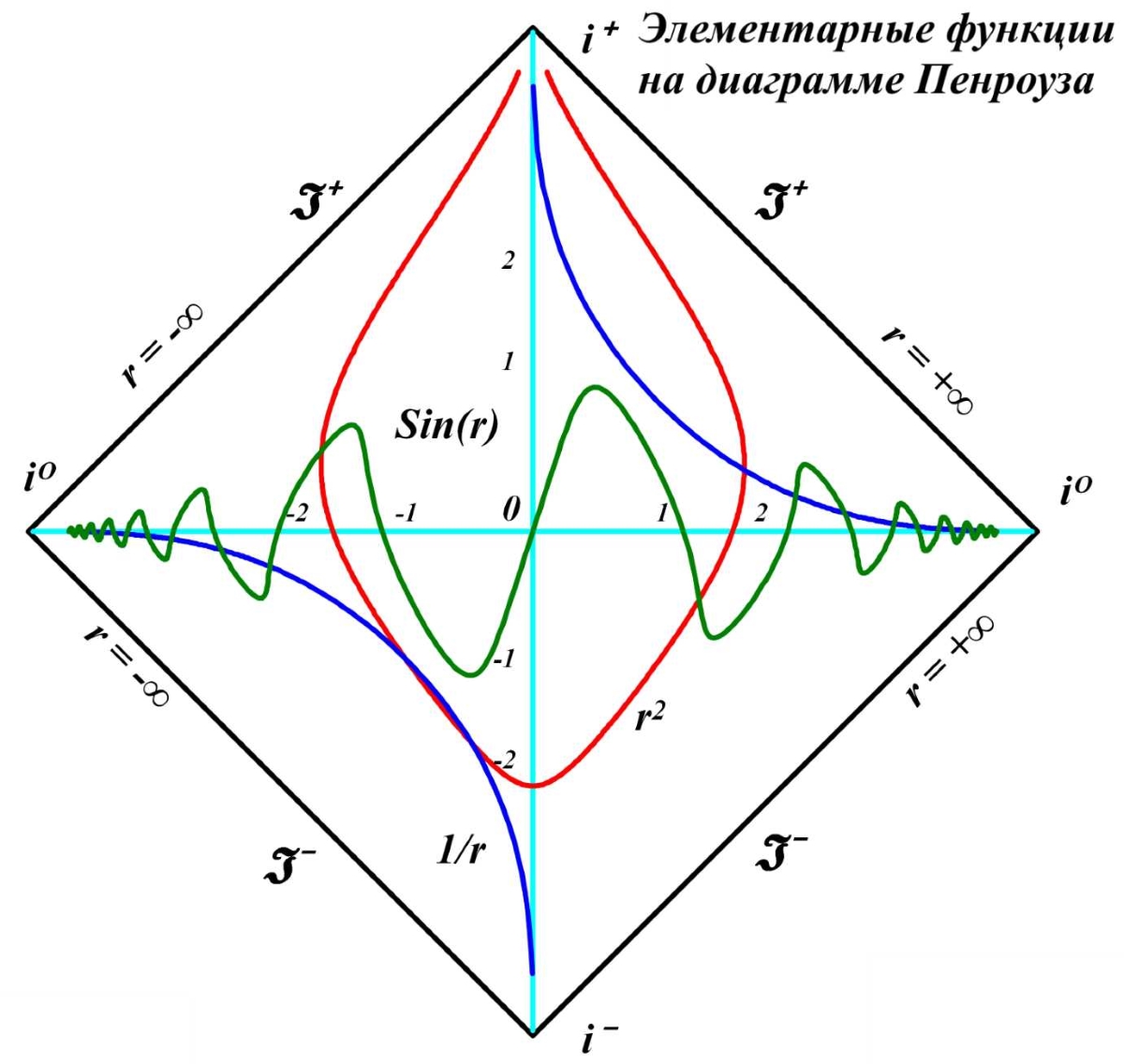 Рис.11. Изображение на диаграмме Пенроуза графиков функций - sin(г), гиперболы 1/r и параболы r2 Добавим, что универсальными изобразительными свойствами обладают также и другие релятивистские системы координат, например, координаты Крускала. В этих координатах размеры фигур ограничены рамками полотна, координатной сетки. Для примера на рисунке рис.12d-g также условно изображены традиционный гиперкуб - тессеракт, синусоида и секундомер, который аналитически, в уравнениях представляет собой обычную окружность. 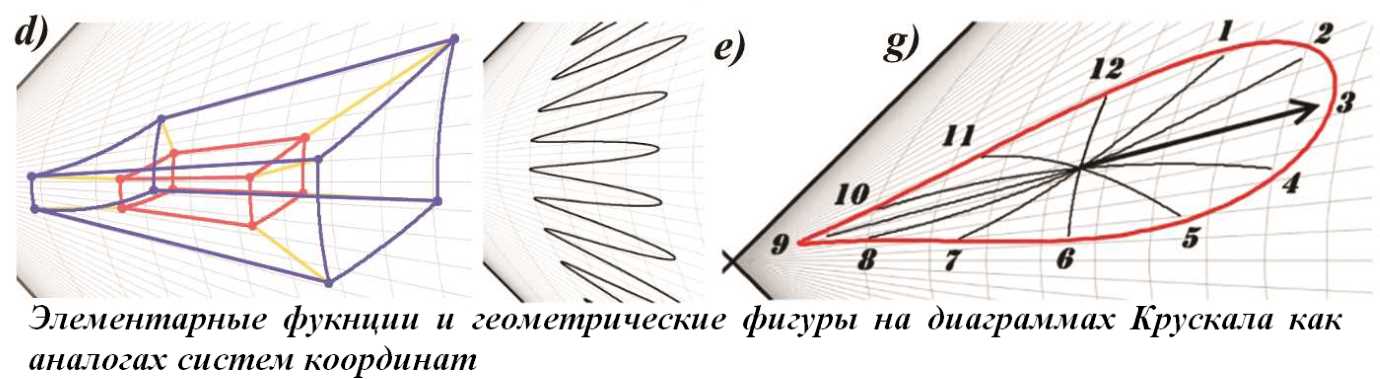 Рис.12. Фигуры на диаграммах Крускала Очень интересно на диаграмме Пенроуза выглядит наипростейшая геометрическая фигура - круг. На рис.13 он изображен в виде стилизованного секундомера, который приобрел довольно забавные очертания, деформируясь в некоторое подобие квадрата. 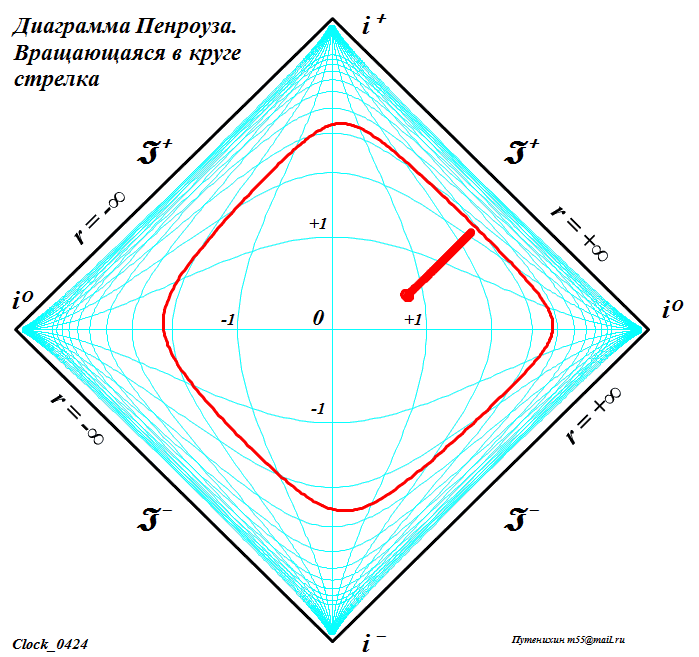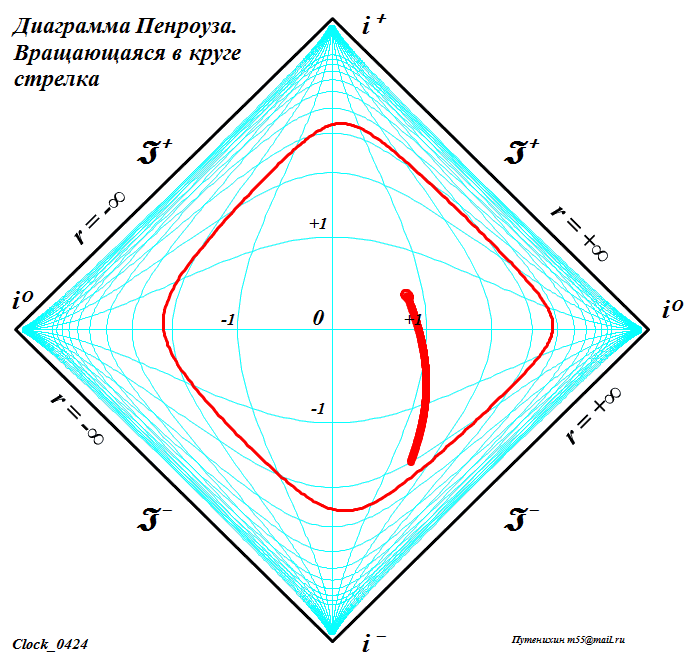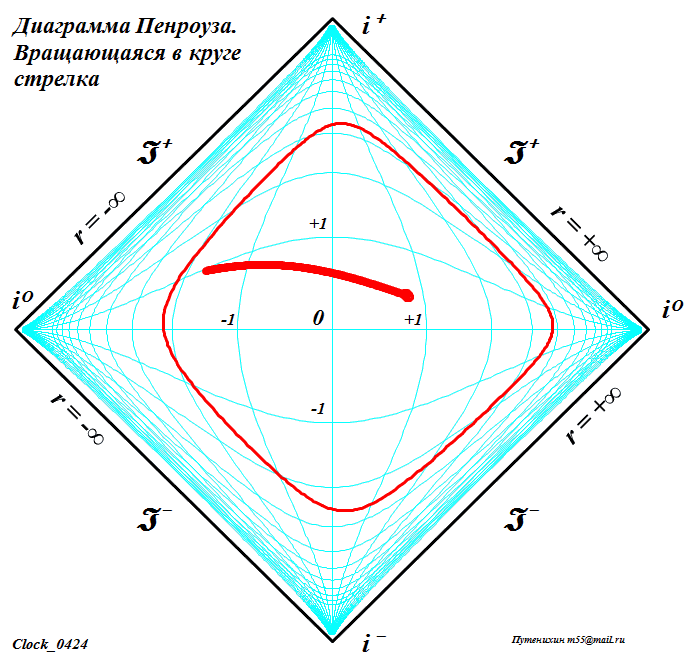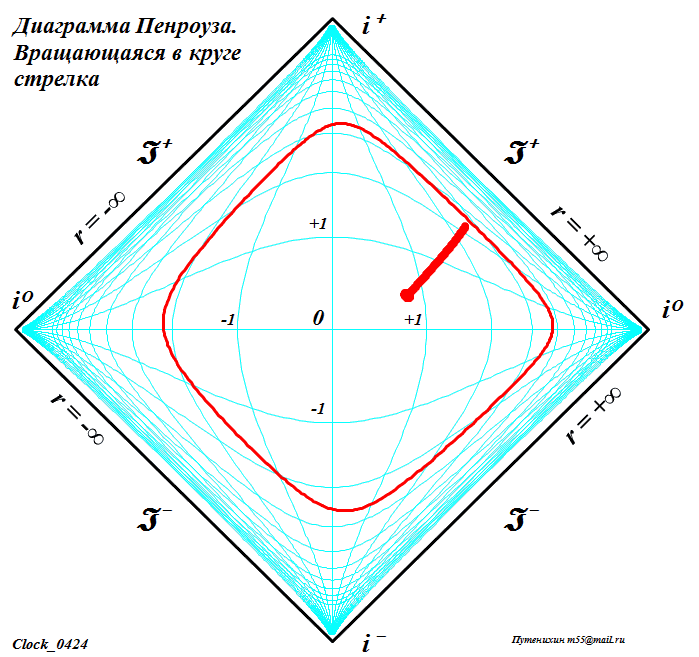 Рис.13. Диаграмма Пенроуза для вращающейся в круге стрелки Трудно представить, но на рисунке действительно изображен круг с вращающейся внутри стрелкой. Особенно забавно картина выглядит на анимации. В процессе движения по окружности стрелка постоянно изгибается - образуя горб то по ходу движения, то против него. И только в четырех точках своей траектории стрелка превращается в прямую линию - на светоподобных траекториях. Как и в случае диаграммы с бесконечными горизонтами, 2М-диаграмма так же является просто координатной системой, ничем принципиально не отличающейся от декартовой. Поэтому и здесь мы вполне можем рассматривать в качестве координат не время и радиус, а обычные декартовы координаты x-y. Однако в этом случае возникает интересный вопрос. На таких 2М-диаграммах Пенроуза имеется обнаруженная ранее право-левая анизотропия, полярность времени [4]. Интересно выяснить, каким образом она проявится в этом координатном случае? Каждому значению x, согласно анизотропии диаграммы, должны соответствовать два разных значения y. Для уравнений "прямых" линий всё, вроде бы, останется по-прежнему - величина зависит от скорости изменения функции. Но как быть с единичной точкой, об истории которой ничего не известно? Допустим, нам нужно изобразить два отрезка с одинаковыми координатами концов. Очевидно, что точки отрезка будут изображаться последовательно, а это уже движение, имеющее и направление и скорость. Вот его и можно использовать. Однако это не обязательно. Если использовать оба значения параметра анизотропии m, то будут изображены два симметричных, зеркальных объекта. Эти объекты зеркальны относительно оси m = 0, а их диаграммные координаты однозначно определены соответствующими параметрами анизотропии m и n. Таким образом, имея функции преобразования, можно построить любую геометрическую фигуру. Давайте построим "секундомер", такой же, как на диаграммах с бесконечными горизонтами рис.13. Построение "секундомера" можно произвести симметрично как с пересечением двух изображений друг с другом, так и без пересечения, когда каждое из изображений будет полностью находиться в одной из областей - выше или ниже оси m = 0. Мы построим только одно полноразмерное изображение каждого из выбранных объектов для одного из значений знака m - рис.14. На рисунке изображены три объекта - две окружности, внутри которых вращаются стрелки - указатели, наподобие секундомеров, и группа из концентрических окружностей. Отметим со всей определенностью, что на рисунке изображены только окружности (и пара стрелок - указателей). Левая, каплевидная синяя окружность имеет радиус R = 0.6, а центр её расположен в точке с координатами x = 3, y = 0.1. Длина указателя или радиус окружности, которую описывает его конец, равны 0.53. Параметр преобразования m имеет положительный знак. Все геометрические параметры фигур, их размеры выбраны такими, чтобы они занимали достаточно большую область рисунка. 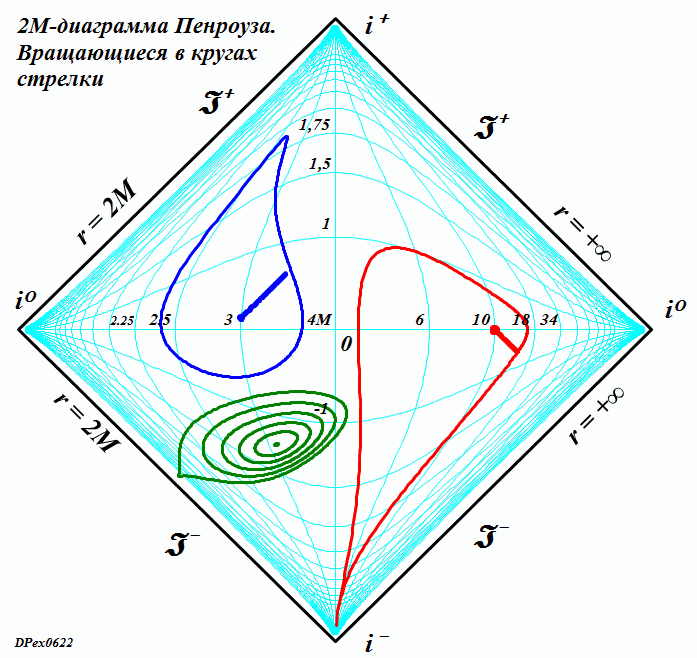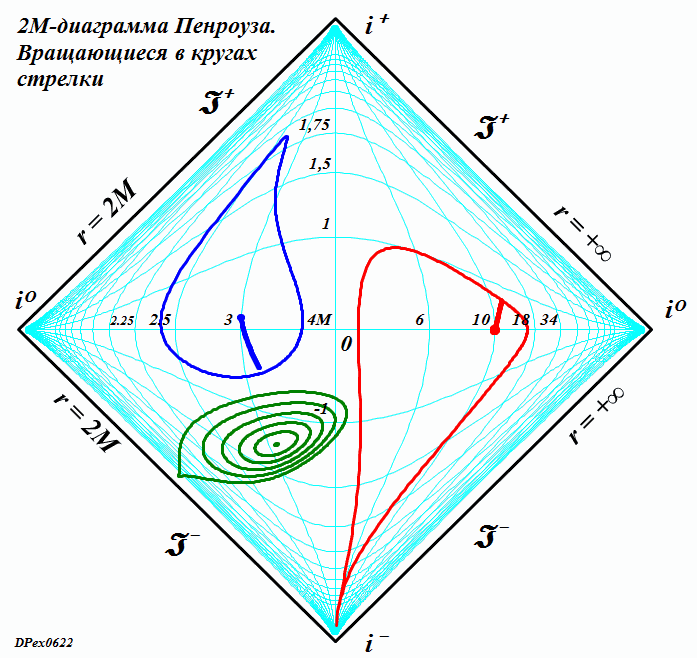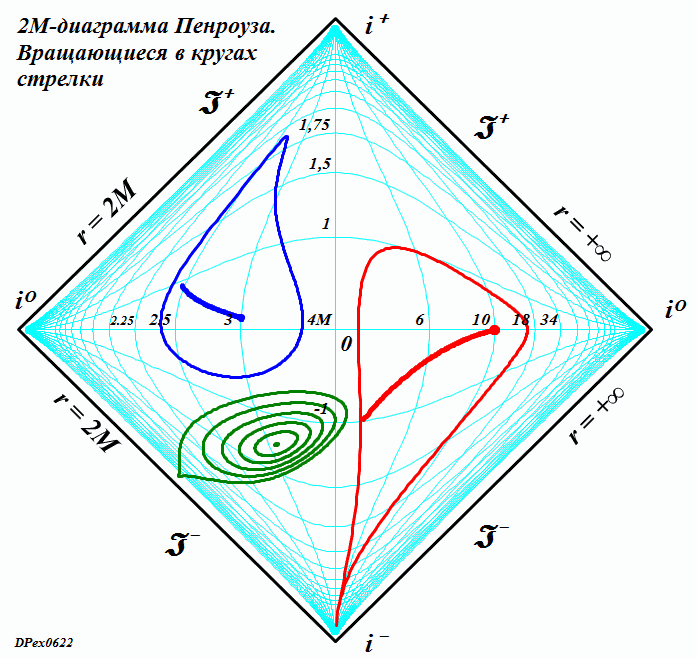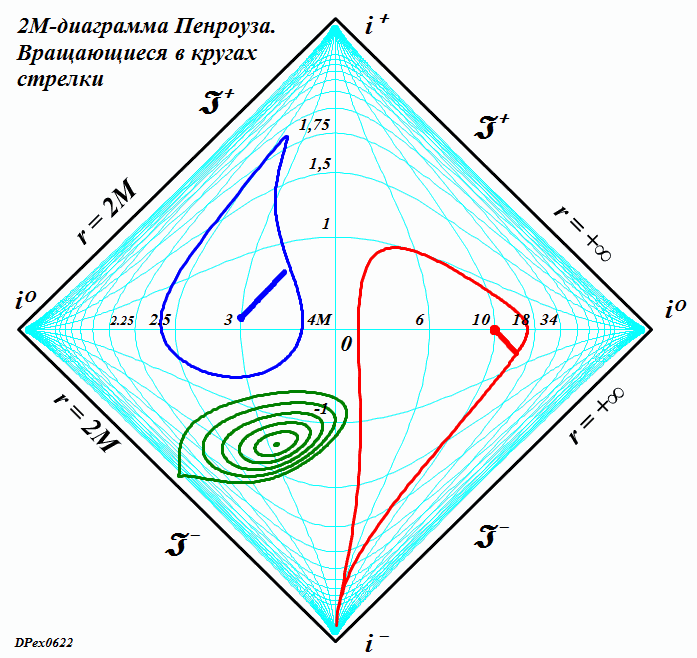 Рис.14. Секундомеры на координатной 2М-диаграмме Обратим внимание, что диаграмма явно "чувствует" знак параметра, поскольку в данном случае указатель секундомера на анимации движется в правильном направлении, по часовой стрелке. Однако, если мы принудительно поменяем знак параметра, то картинка просто перевернётся, зеркально отразившись от оси x. В этом случае направление движения указателя также изменится на противоположное. Этот переворот виден на правой стороне диаграммы. Фрагмент отдаленно напоминает картину "Твердость памяти" Сальвадора Дали с "плавящимися часами". У нас на диаграмме, как и выше, так же изображен круг, в котором вращается стрелка - указатель. Параметры окружности: радиус R = 5.66, а центр имеет координаты x = 10, y = 0. Длина указателя или радиус окружности, которую описывает его конец, равны 5,6. Знак параметра m выбран отрицательным и диаграмма это вновь "почувствовала", направив вращение указателя против часовой стрелки. Если для этой окружности мы выберем знак параметра m положительным, то "секундомер" просто отразится зеркально от оси x, а указатель будет вращаться, как положено - по часовой стрелке. Слева внизу диаграммы для наглядности изображена группа концентрических окружностей. Все визуальные деформации связаны исключительно с криволинейностью системы координат 2М-диаграммы. Заключение Итак, основная, фундаментальная сущность диаграмм Пенроуза состоит в отображении на квадрат конечных размеров бесконечного одномерного пространства-времени. По сути, это обычная координатная система одномерного пространства, поскольку время не является пространственной координатой. Используя все те же средства, что и на традиционных диаграммах Минковского, мы можем изобразить те же самые мировые линии. Используя уравнения преобразования координат, мы можем изобразить на диаграмме Пенроуза любую мировую линию, график вообще любой функции целиком. Для этого нам нужно знать только уравнение её движения r(t). Более того, мы можем нарисовать последовательность диаграмм для каждого момента времени по этим уравнениям, которые затем можно соединить в динамическую последовательность кадров, в анимацию. Часть 1. URL: http://moianauka.ru/load/2-1-0-1521 Литература 1. Хокинг С., Эллис Дж., Крупномасштабная структура пространства-времени. М.: "Мир", 1977. 2. Хокинг С., Пенроуз Р. Природа пространства и времени. -- Ижевск: НИЦ "Регулярная и хаотическая динамика". 2000. 160 с. 3. Путенихин П.В., Динамические диаграммы Минковского на примере обмена световыми сигналами, 2014, URL: http://samlib.ru/p/putenihin_p_w/ddm-light.shtml 4. Путенихин П.В., Показательная функция для 2м-диаграммы Пенроуза, 2019, URL: http://samlib.ru/editors/p/putenihin_p_w/exp33.shtml 5. Путенихин П.В. Диаграммы Пенроуза. Анализ и критика. -- Саратов: "АМИРИТ", 2017. - 176 с., цв. илл., URL: https://www.twirpx.org/file/3078810/ https://www.elibrary.ru/item.asp?id=42733192 | |
| Категория: Разное | | | |
| Просмотров: 1738 | Загрузок: 513 | |
| Всего комментариев: 0 | |