Путенихин П.В. Вселенная расширяется замедленно?
| [ Скачать с сервера (6.86 Mb) · Скачать удаленно (7,2 Mb) · Скриншот ] | 03.06.2021, 13:24 |
Введение 11. Исследование переменных параметров Хаббла 11.1. Наблюдаемые диаграммы Хаббла 11.2. Параметр Хаббла с изгибом 11.3. Проблема сверхсветового движения Диаграммы для действительных источников 11.4. Спорные выводы об ускоренном расширении Выводы 12. О возрасте Вселенной Аннотация Считается, что одним из главных аргументов, из которого следует вывод об ускоренном расширении Вселенной, является пониженная яркость дальних сверхновых. Математическое исследование этого явления неожиданно привело к прямо противоположному выводу. Если дальние сверхновые видны более тусклыми, то Вселенная расширяется с замедлением. Is the universe expanding decelerating? It is believed that one of the main arguments from which the conclusion about the accelerated expansion of the Universe follows is the reduced brightness of distant supernovae. A mathematical study of this phenomenon unexpectedly led to the exact opposite conclusion. If distant supernovae are seen dimmer, then the universe is expanding decelerate. Фрагмент для ознакомления Введение Существует предположение, что Вселенная расширяется в наши дни с ускорением, а в более далёком прошлом, напротив, она расширялась замедленно. Какими наблюдениями можно подтвердить это? Считается, что одним из главных аргументов, обосновывающих ускоренное расширение Вселенной, является пониженная яркость дальних сверхновых. Однако это правило выглядит довольно необычно. В самом деле, если они более тусклые, то они находятся дальше, что соответствует скорее их более быстрому удалению в прошлом. Хотя приведённое правило "тусклый-дальний" в целом корректно, правильнее всё-таки говорить, что при ускоренном расширении сверхновые имеют меньшую скорость, меньшее красное смещение, чем этого требует стандартный закон Хаббла. Хотя удалились они на меньшее расстояние, находятся они ближе, чем в равномерно расширяющейся Вселенной. Действительно, несложный анализ показывает, что при ускоренном расширении Вселенной и на самом деле любой объект оказывается на более близком удалении, проходит меньший путь, нежели при замедленном или равномерном расширении. Давно замечено одно интересное и важное свойство математики – делать верные описания нашего мира, предсказания, на первых порах кажущиеся буквально выдумками: "... почему математика столь эффективна при описании нашего мира и столь хорошо описывает его эволюцию? ... Почему эти правила так хорошо работают?" (Линде) Вряд ли следует слишком уж сильно этому удивляться. Эта математика так хорошо работает просто потому, что мы и вывели её из прямых наблюдений за окружающей действительностью. Эффективно работает, значит, верно подсмотрели. Более того, в науке и в физике, в частности, уже давно замечена еще одна интересная закономерность: кажущиеся поначалу абстрактными математические выражения, уравнения вдруг оказываются описанием какого-нибудь вполне реального явления: "... физики обнаруживают, что математические построения, необходимые им для описания нового класса явления, уже исследованы математиками по причинам, не имеющим ничего общего с обсуждаемыми явлениями" (Виленкин). Однако даже при таком явно полезном подходе следует все-таки быть предельно осторожным при формулировке выводов и следствий из этих математических построений. Можно привести ряд примеров, когда такие выкладки приводят не просто к противоречиям со здравым смыслом, но к довольно заметным противоречиям с логикой, содержат логические ошибки. В предлагаемой работе мы покажем, что математические выводы в физике во многом зависят как от их последующей трактовки, так и от предположений, оснований, исходных положений, использованных в процессе получения этих выводов. Вообще говоря, это очевидно: если изменить исходные положения, заявить истинными другие, выводы также будут иными, а то и противоположными. Но какие из этих взаимоисключающих выводов верны? Нас интересуют логические построения, послужившие основой для утверждения об ускоренном расширении Вселен-ной, опирающиеся на факт пониженной яркости дальних сверх-новых. Поскольку детали этой логики нам неизвестны, мы про-ведём собственные построения, пытаясь прийти к такому же выводу, утверждению. В дальнейшем мы используем следующую систему обо-значений. Все дистанции мы измеряем в миллиардах световых лет, а время – в миллиардах лет. В этом случае скорость света равна единице. Обозначение шкалы скоростей v/c и означает, что значения представлена в долях от скорости света. У переменных, параметров и графиков нижние индексы состоят из букв и их комбинаций: a – ускорение (accelerate); d – замедление (decelerate); s – условная стационарность, на отдельном участке; о – неизменный, обычный, традиционный. Например, ad – обозначает ускорение – замедление и наоборот. Возможны и более длинные индексы, поскольку некоторые параметры на всём протяжении состоят из нескольких участков: ada – ускорение, замедление, ускорение. Последний индекс - o, по сути, является эквивалентом нуля, используемый просто для удобства записи. То есть, Ho и H0 – это один и тот же параметр Хаббла в нашей Вселенной. Некоторые параметры имеют отдельные обозначения: Rф – график движения фотонов в системе отсчёта сверхновой; Rco – путь, пройденный фотонами по их измерениям; Rc и Vc – графики движения условного источника фотонов, пройденный им путь и его скорость. Большинство параметров на приводимых диаграммах за-висят от времени, однако эту зависимость в их обозначениях для краткости мы чаще всего опускаем. Все рассмотренные Вселенные и параметры их расширения являются вымышленными, условными и имеют к настоящей, нашей Вселенной лишь качественное, демонстрационное отношение. При этом на одной диаграмме для сопоставления будут изображены параметры движения сразу нескольких Вселенный, никак не связанных друг с другом. 11. Исследование переменных параметров Хаббла Построим диаграммы Хаббла для расширения Вселенной с каждым из этих параметров, используя выведенный в предыдущих разделах алгоритм определения удалённости объектов с учётом времени в пути света от них до наблюдателей на Земле. Для наглядности изобразим диаграммы с приведёнными на рис.11.1 параметрами на одном рисунке: Ro для равномерно расширяющейся Вселенной с параметром H0; Rd для Вселенной, расширяющейся замедленно с убывающим параметром Хаббла Hd; диаграмму Ra для Вселенной с параметром Ha, возрастающим от некой произвольной малой величины до современного значения, и теоретическую диаграмму Хаббла R(v): 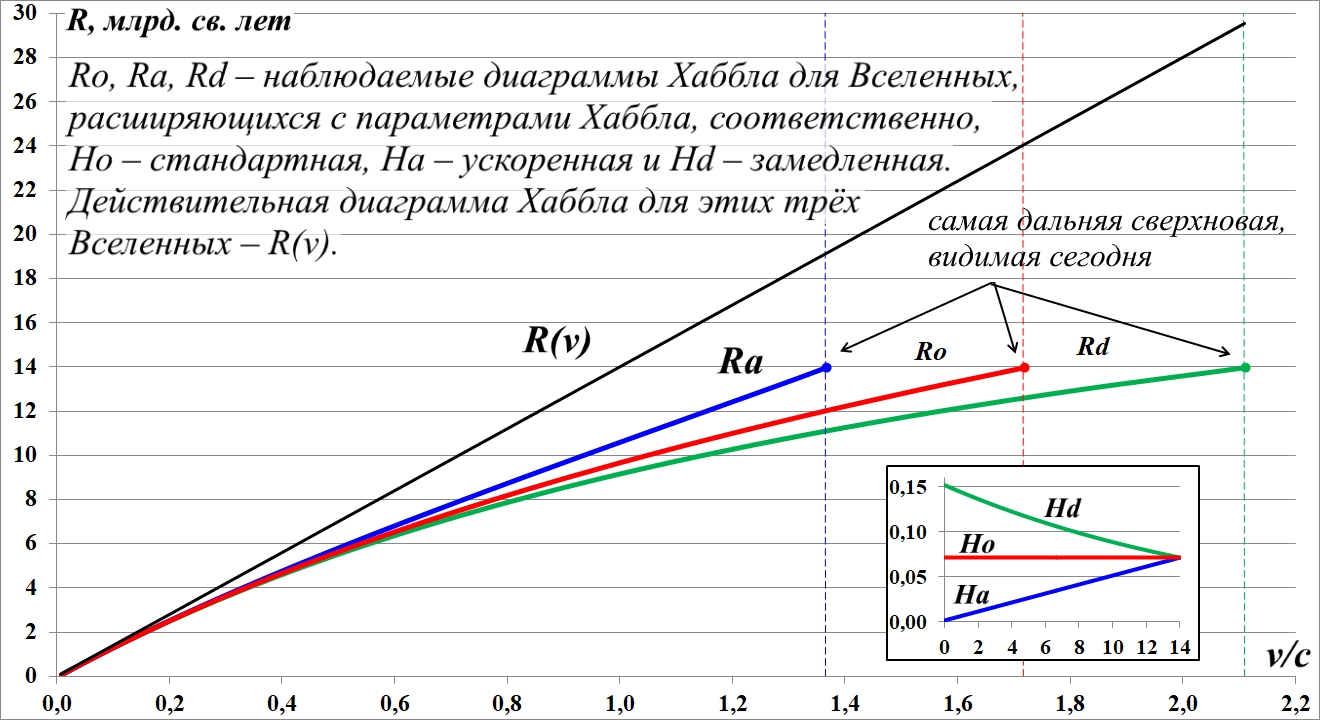 Рис.11.2. Наблюдаемые диаграммы Хаббла для Вселенных с параметрами H0, Hd и Ha. На рисунке чёрный график R(v) – это слившиеся в один графики теоретического закона Хаббла для Вселенной с H0 и теоретических графиков законов Хаббла для Вселенной с убывающим, Hd и с возрастающим, Ha параметрами Хаббла. Это слияние индивидуальных теоретических графиков Хаббла, собственно говоря, достаточно очевидно, поскольку является следствием того, что в конечной точке, в наши дни все параметры равны H0, и диаграммы соответствуют именно этому моменту времени, когда во всей Вселенной объекты удаляются друг от друга именно с этим параметром Хаббла. При этом отметим некоторую условность: мы принимаем, что скорость источника фотонов равна скорости удаления сверхновой на момент наблюдения фотонов. Как видим, взаимное положение графиков, диаграмм Хаббла сохранилось, но теперь ни один из них не является прямой линией, как на рис.11.1 и как на стандартной диаграмме. При этом замечаем, что графически при некоторой произвольной скорости сверхновой параметр Хаббла H0 для красного графика больше, чем для зелёного Ha, и меньше, чем для синего Hd. Диаграммы для действительных источников Такая корректировка прошла успешно и мы получили требуемый инверсный параметр Hda. Строим диаграмму Хаббла на его основе и обнаруживаем, что с такой зависимостью мы получаем известное соотношение: дальние сверхновые теперь видны более тусклыми, а сверхдальние, напротив, со временем замедляют скорость своего разбегания, рис.11.13. Падение параметра Had происходит по выпуклой параболе, что приводит к его резкому уменьшению в наши дни. Предполагаем, что более естественным было бы его падение по экспоненте или гиперболе. Наш регулируемый параметр Hda ~ Had не позволяет скорректировать этот участок, поскольку он функционально задан параболой. 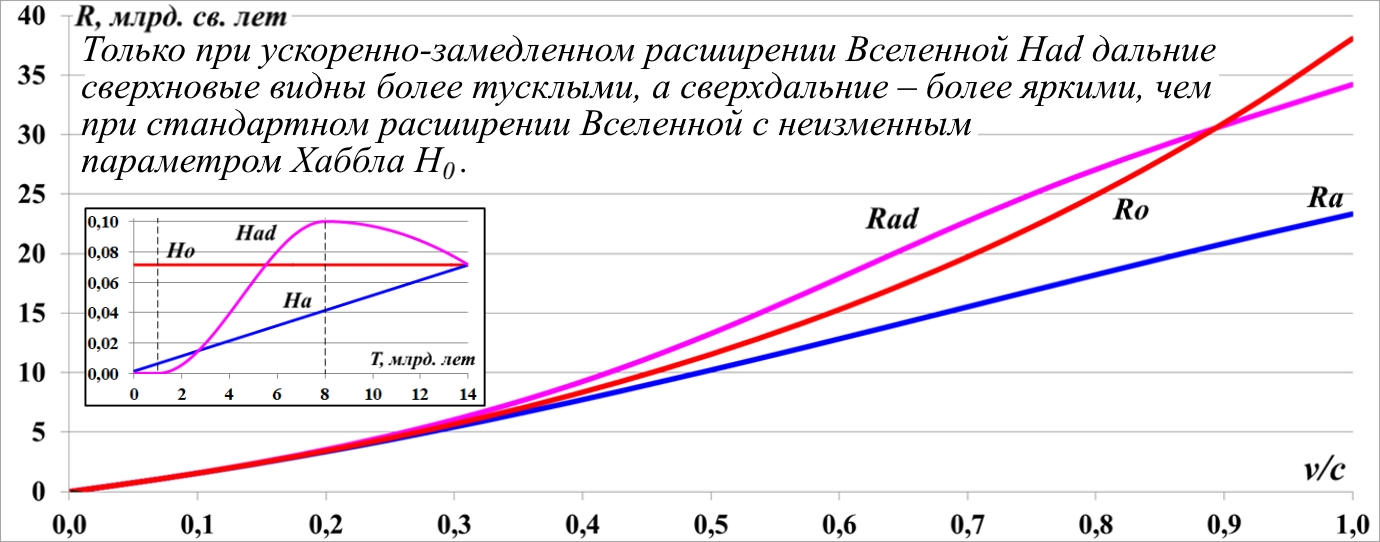 Рис.11.13. Только при ускоренно-замедленном расширении Вселенной с параметром Had дальние сверхновые видны более тусклыми, а сверхдальние – более яркими Для простоты сформируем этот параметр Had из прямолинейных отрезков, выбрав 14 интервалов. Такой способ формирования параметра позволяет подогнать его форму под любой вид диаграммы Хаббла. В результате удалось получить диаграмму, соответствующую утверждению об ускоренном расширении Вселенной: тусклые дальние сверхновые и более яркие – сверхдальние. 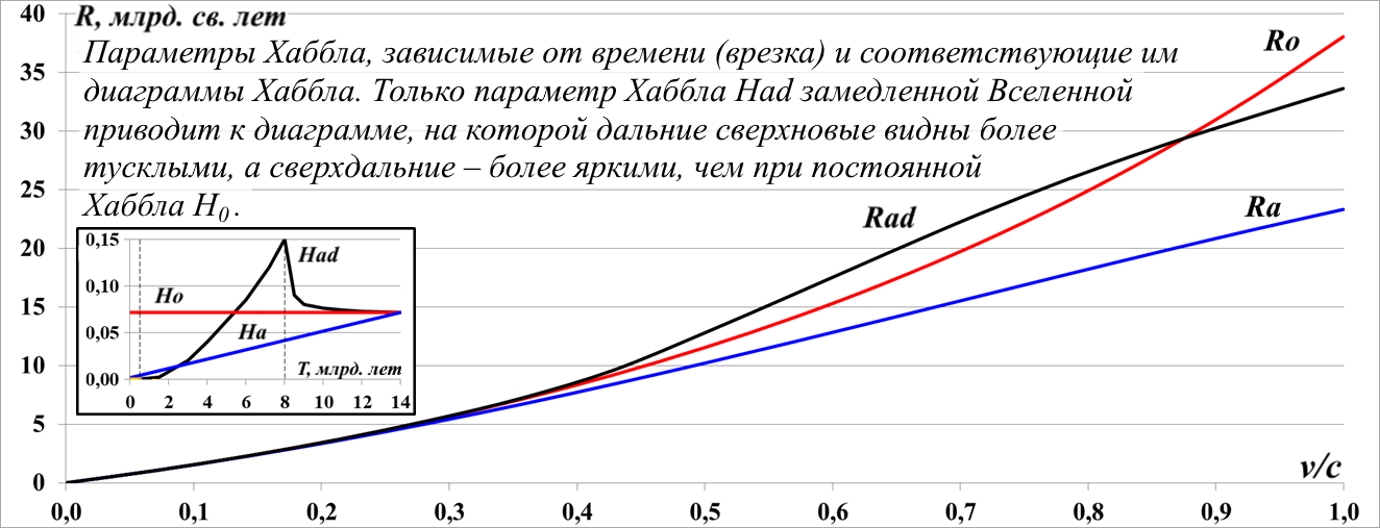 Рис.11.14. При ускоренно-замедленном расширении Вселенной с параметром Had дальние сверхновые видны более тусклыми, а сверхдальние – более яркими. Параметр представлен в виде ломаной линии Однако и в этот раз мы обнаруживаем, что сам параметр Хаббла соответствует противоположному характеру расширения Вселенной – замедленному. Вселенная сначала расширяется ускоренно, затем замедленно. Буквально это означает, что в наши дни согласно наблюдениям за тусклыми сверхновыми мы получаем замедленное расширение Вселенной. 11.4. Спорные выводы об ускоренном расширении Поскольку параметр Хаббла Hd также имеет настроечные величины для пика и минимума, мы проделали такую же процедуру подбора и с ним. Оказалось, что его регулировкой наугад можно получить вид диаграммы Хаббла, довольно близко приближающийся к виду диаграммы ускоренного расширения Вселенной, рис.11.18. Отметим, что правильнее было бы параметр Хаббла в этом случае именовать Hada. Единственным, неуверенно слабым местом этой диаграммы является участок ближних сверхновых. Хотя и очень слабо, но можно заметить их некоторую повышенную яркость по отношению к стандартной диаграмме Хаббла. Лучше всего это заметно на увеличенном фрагменте диаграммы рис.11.19. 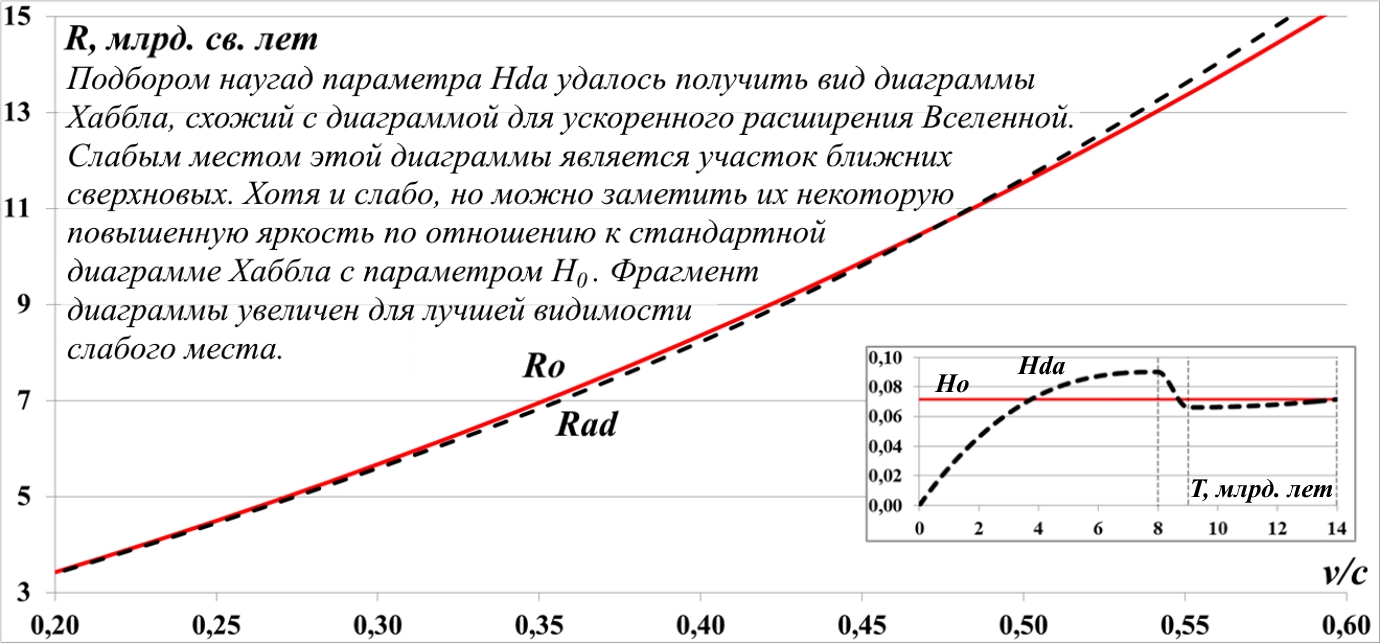 Рис.11.19. Увеличенный фрагмент диаграммы для замедленно-ускоренного расширения Вселенной с параметром Hda. Ближние сверхновые видны с повышенной яркостью. Обращаем внимание, что в соответствии с отрицательным знаком параметра Хаббла такая условная Вселенная на начальном этапе не расширялась, а сжималась, график R(t). Иначе говоря, изначально она обладала отрицательной скоростью v(t), которая в наши дни изменила направление и достигла скорости света. Свет от вспышки сверхновой распространялся практически так же, как в стационарной Вселенной. По графикам мы видим, что пути фотонов – фактический Rco и хаббловский Rф – практически не различаются, поэтому влияние поперечного хаббловского расширения светового потока сводится к обычному закону обратных квадратов. Наблюдаемые удалённость Rco и скорость Vc также практически совпадают с теоретическими значениями R(t) и v(t), соответственно. Лишь спустя 8 млрд. лет расширение Вселенной стало заметным, а спустя 12 млрд. лет скорость расширения резко возросла. В последний миллиард лет наша условная Вселенная вновь стала расширяться с замедлением вплоть до наших дней. Хотя Вселенная выглядит отчасти как стационарная, диаграммы Хаббла отчётливо показывают зависимость красного смещения, скорости сверхновых от их удалённости. Причём осталась в силе метафора "дальние сверхновые более тусклые". И, соответственно: сверхдальние, наоборот, более яркие. Выходит, что в классическом, прямолинейном виде диаграмма Хаббла R(v) = Rs(v) будет в нашей реальной Вселенной наблюдаема только в случае параметра Хаббла H0(t) = Hs, имеющего форму латинской буквы L, лежащей "на спине". Именно с таким параметром Хаббла диаграмма будет иметь классический вид рис.11.24: 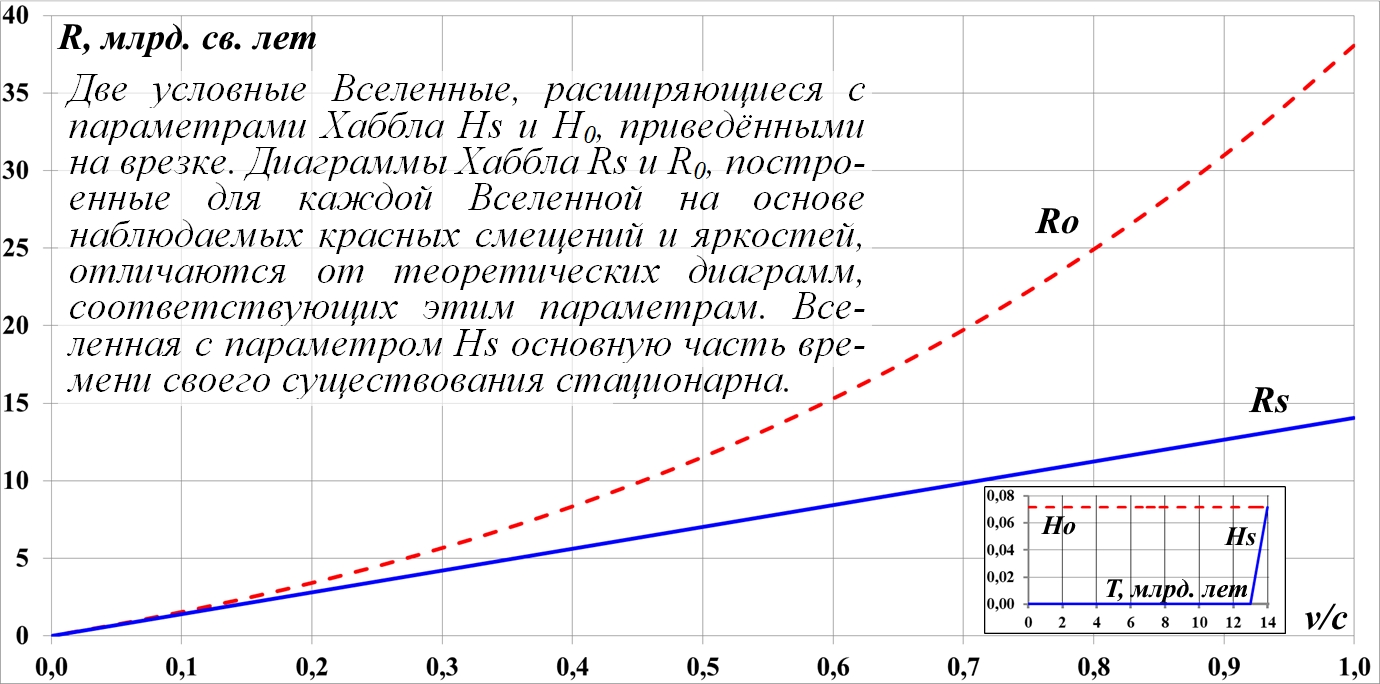 Рис.11.24. Наблюдаемые диаграммы Хаббла для Вселенных с параметрами H0 и Hs. Диаграмма Rs соответствует Вселенной, которая большую часть времени была стационарной На рисунке представлены две диаграммы Хаббла, а на врезке – соответствующие им параметры Хаббла. Обе диаграммы являются наблюдаемыми, результаты измерения скорости и яркости каждой сверхновой в своей Вселенной в точности лягут на соответствующую линию. Однако на самом деле их реальные, действительные удалённости и скорости удаления будут иными. Отметим, что Вселенная с параметром Hs основную часть времени существования является стационарной. Выводы Вывод об ускоренном расширении Вселенной по признаку пониженной яркости дальних сверхновых одинаково справедлив как при ускоренном, так и при замедленном реальном, фактическом расширении Вселенной. О действительной скорости расширения Вселенной нельзя судить только лишь по разнице наблюдаемых параметров Хаббла в далёком прошлом и в наши дни, это ускорение – замедление является кажущимся. Такая же неопределённая картина наблюдается и в случае первично стационарной Вселенной с L-образным параметром Хаббла Hs. Такая условная Вселенная была стационарной 13 млрд. лет, после чего начала стремительно расширяться до современного значения параметра Хаббла – H0. Иначе говоря, форма параметра Hs напоминает латинскую букву L, лежащую "на спине". При этом по наблюдаемым данным, яркости и красному смещению будет формироваться традиционная, прямолинейная диаграмма Хаббла. Производный от этой диаграммы параметр Хаббла будет неизменным и равным современному значению параметра Хаббла H0 в нашей Вселенной. В действительности же такая Вселенная большее время была стационарной. И при ускоренном и при замедленном расширении в такой условно стационарной Вселенной отличие диаграмм от "базовой", с L-образным параметром Hs, являющимся эквивалентом параметра H0 нашей Вселенной, точно так же будет наблюдаться эффект "дальняя – более тусклая" и "сверхдальняя – более яркая". Правда, модель ускоренного расширения пространства в такой Вселенной имеет "дефект", пусть и слабый, но всё-таки понижающий её достоверность – это повышенная яркость ближних сверхновых. Во всех случаях приоритетной моделью, видимо, следует считать модель замедленного расширения Вселенной. | |
| Категория: Разное | | | |
| Просмотров: 1746 | Загрузок: 558 | |
| Всего комментариев: 0 | |