Путенихин П.В. Квантовый гейт CNOT
| [ Скачать с сервера (1.81 Mb) · Скачать удаленно (1,81 Mб) · Скриншот ] | 01.06.2021, 17:24 |
Аннотация: Рассмотрена модификация традиционной установки для телепортации квантового состояния кубита. На передающей стороне изменена на противоположную последовательность гейтов CNOT и гейта Адамара. Модифицированная установка позволяет телепортировать теперь уже не просто неизвестное состояние кубита, а состояние запутанности кубитов. На стороне передатчика установка переводит два кубита в состояние запутанности, в результате чего и на стороне приемника два кубита также оказываются в состоянии запутанности. Показана также возможность непосредственной сверхсветовой передачи классической информации с помощью гейта CNOT. A modification of the traditional setup for teleporting the quantum state of a qubit is considered. On the transmitting side, it is changed to the opposite sequence of the CNOT gates and the Hadamard gates. The modified installation allows you to teleport now no longer just an unknown state of the qubit, but a state of entanglement of qubits. On the transmitter side, the installation translates two qubits into a state of entanglement, with the result that, at the receiver side, two qubits also end up in a state of entanglement. It is shown also the possibility of direct superluminal transmission of classical information using the gate CNOT Оглавление Введение Создание запутанных состояний гейтом CNOT Телепортация запутанности Квантовый семафор Передача сигнала нуля Передача сигнала единицы Заключение Библиографические ссылки Введение Явление запутанности непосредственно следует из математического формализма квантовой механики. В соответствии с первым постулатом квантовой механики состояние квантовой частицы полностью описывается её волновой функцией. Однако в некоторых случаях квантовым частицам не удаётся приписать индивидуальные волновые функции, а только одну на всех. Такое состояние частиц названо запутанностью. Это состояние удалось получить на реальных частицах, например, в так называемых процессах параметрического распада, преобразования с понижением частоты (down conversion) на специальных кристаллах. Физическое проявление запутанности в формализме квантовой механике получило собственное имя - нелокальность как антагонизм так называемому локальному реализму Эйнштейна, который не допускал пространственноподобной зависимости между запутанными частицами. Он предполагал, что экспериментально наблюдаемая связь между частицами на самом деле формируется в момент их запутывания и сохраняется до конца опыта. То есть, случайными состояния частиц формируются в момент их разделения. В дальнейшем они сохраняют полученные при запутывании состояния, и "хранятся" эти состояния в неких элементах физической реальности, описываемых "дополнительными параметрами", поскольку измерения над разнесенными системами не могут влиять друг на друга: "Но одно предположение представляется мне бесспорным. Реальное положение вещей (состояние) системы S2 не зависит от того, что проделывают с пространственно отделённой от неё системой S1" [4, c.290]. "... так как во время измерения эти две системы уже не взаимодействуют, то в результате каких бы то ни было операций над первой системой, во второй системе уже не может получиться никаких реальных изменений" [5, с.608]. К истокам возникновения таких взглядов на квантовую механику можно по праву отнести парадокс Эйнштейна-Подольского-Розена (ЭПР-парадокс), которые считали, что квантовая механика неполна, поскольку обнаруженная сверхсветовая корреляция запутанных частиц допускает одновременное определение некоммутирующих параметров системы, запрещаемое формализмом теории. Именно эти предположения и получили в дальнейшем название локального реализма Эйнштейна: "Насчет того, что понимать под нелокальностью в КМ, то в научной среде, я считаю, сложилось некоторое согласованное мнение на этот счет. Обычно под нелокальностью КМ понимают то обстоятельство, что КМ противоречит принципу локального реализма (его еще часто называют принципом локальности Эйнштейна). Принцип локального реализма утверждает, что если две системы A и B пространственно разделены, тогда при полном описании физической реальности, действия, выполненные над системой A, не должны изменять свойства системы B" [3]. Нелокальность, мгновенная корреляция между запутанными квантовыми частицами является одним из самых загадочных явлений физики. Буквально её сущность можно выразить фразой "связь есть, но её нет". Проявляется эта связь при передаче так называемой квантовой информации между запутанными парами квантовых частиц. При измерении состояния одной из частиц пары вторая частица мгновенно и на пространственноподобном расстоянии также переходит в собственное состояние, будто и над ней произведена операция измерения. При этом состояние второй частицы строго коррелировано с состоянием первой. Получается, что первая частица как бы передает второй частице некоторую информацию со сверхсветовой скоростью. Собственно носитель этой информации зарегистрировать в настоящее время не удалось, поэтому передача информации посредством нелокальной связи считается невозможной. На роль носителя этой неуловимой квантовой информации может претендовать гипотетическая частица - тахион, также не обнаруженный ни в одном эксперименте. Вместе с тем возникает некоторая взаимосвязь явлений: если происходит какое-то взаимодействие со сверхсветовой скоростью, которое обнаружено в реальном физическом эксперименте - квантовая телепортация, то мы обязаны признать, что существует и некий реально существующий физический, материальный носитель этой информации. Следовательно, должна существовать и возможность сверхсветовой передачи уже не только мистической квантовой информации, но и реальной, классической информации. Как известно, явление квантовой телепортации обнаружено исключительно математическими средствами в рамках квантовой информатики. Уравнения любых допустимых унитарных преобразований квантовых систем, то есть, преобразований, не приводящих к переходу квантовых частиц в собственные состояния, не содержат параметра времени и расстояний. Это ведет к естественному предположению о мгновенной передаче состояний объектов связанной, единой квантовой системы друг другу, причем на любом расстоянии. На основе аналитических уравнений была разработана установка для передачи состояния от одной частицы запутанной пары к другой. Передаваемое состояние является произвольным и может быть неизвестно передающей стороне. Но проблема не в этом: даже зная состояние передаваемой частицы, мы не можем мгновенно узнать состояние частицы, переданное удаленной стороне. Это возможно лишь с использованием дополнительной, классической информации. Иначе говоря, считается строго доказанным, что сверхсветовая передача классической информации посредством квантовой телепортации невозможна. Главным аналитическим критерием в этом вопросе стали так называемые неравенства Белла, утверждающие, что никакие вероятностные корреляции невозможны без сверхсветовой передачи информации. Собственно, понятие "неравенства Белла" породила статья Д.Белла "Парадокс Эйнштейна Подольского Розена" была опубликована в 1964 году, В ней Белл произвёл тщательный анализ доводов Эйнштейна, Подольского и Розена. Он убедительно показал, что теории со скрытыми переменными в принципе не позволяют объяснить результаты, полученные в реальных экспериментах. Белл пришёл к выводу: "В квантовой теории с дополнительными параметрами для того, чтобы определить результаты индивидуальных измерений без того, чтобы изменить статистические предсказания, должен быть механизм, посредством которого настройка одного измеряющего устройства может влиять на чтение другого отдаленного инструмента. Кроме того, задействованный сигнал должен распространяться мгновенно ..." [1]. Другими словами, если мы с позиции теории с дополнительными параметрами будем утверждать, что результаты измерений над каждой частицей полностью независимы друг от друга, независимы в физическом смысле, а все совпадения являются статистическими следствиями, то есть, по существу, они всего лишь случайные совпадения, то в этом случае мы будем вынуждены переложить весь груз этой случайности на некий механизм, упомянутый Беллом. Этот механизм должен обладать способностью подстраиваться под измерения со сверхсветовой скоростью. Следовательно, такая теория опять-таки противоречит специальной теории относительности и поэтому тоже отвергает ЭПР-аргументы. Еще один запрет на сверхсветовую передачу классической информации накладывает теорема о запрете клонирования кубита. Клонирование могло бы позволить многократными измерениями клонов определить состояние телепортированного кубита. Вместе с тем, вопрос о непосредственной передаче информации как таковой является до сих пор дискуссионным. В одной из работ этот вопрос формулируется в явном виде: "Подразумевает ли передача нелокальной информации автоматически сверхсветовую сигнализацию?" [2, гл.1.1] Здесь, как видим, фактически между квантовой (нелокальной) и классической информацией не проводится явной границы. Констатируется, что сама по себе передача сверхсветовой информации не приводит к возникновению парадоксов причинности, если эта информация недоступна. Квантовая информация, по крайней мере, в настоящее время таковой и является. Отсюда возникает интересная интерпретация нелокальной информации, как одной и той же информации одновременно присутствующей в двух разных областях пространства. Эта информация как бы объединяет эти области, она становится "пространственно расширенной" [2, гл.6.3]. Несмотря на все эти доводы, аргументы можно провести фундаментальную параллель между квантовой и классической информацией. Хотя носитель квантовой информации в явном виде, в эксперименте не зарегистрирован, есть гипотетическая возможность использования квантовой информации для сверхсветовой передачи информации классической. Создание запутанных состояний гейтом CNOT Помимо косвенной сверхсветовой сигнализации посредством телепортации состояния запутанности можно рассмотреть еще один гипотетический способ непосредственной сверхсветовой коммуникации. С этой целью удобно использовать квантовые гейты CNOT, которые позволяют получить состояние запутанности вместо параметрического распада. Математическое описание этого процесса достаточно наглядно. Схема гейта CNOT представлена на рис.1a - изображение, чаще всего используемое в литературе, на рис.1б - изображение гейта, использованного в схеме традиционной квантовой телепортации (перевернуто). 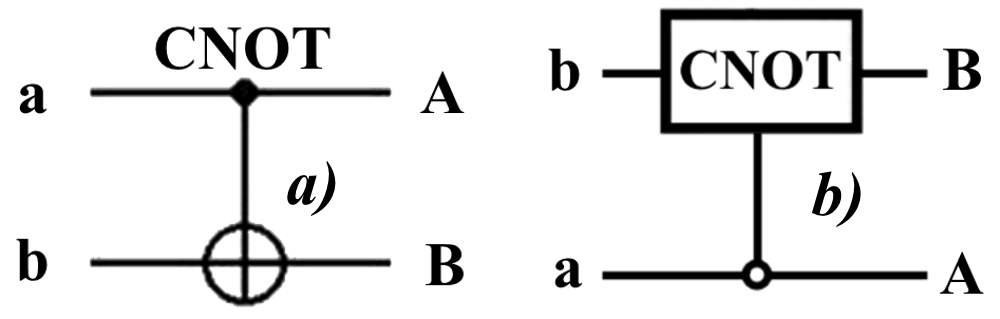 Рис.1. Схема гейта CNOT Обозначения входов и выходов перевернутого изображения гейта, используемого далее в схеме рис.2, полностью соответствуют его традиционной таблице состояний (ниже). Математически этот квантовый оператор описывается выражением: 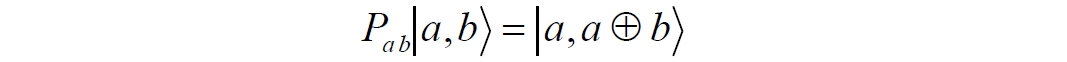 где a⊕b означает логическое сложение по модулю 2. Как видно из выражения, управляющий сигнал проходит со входа на выход без изменений. Матрица преобразования гейта CNOT имеет вид: 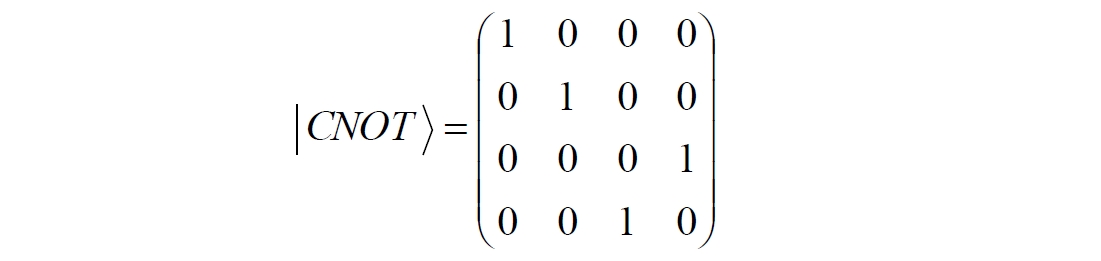 Подадим на управляющий и управляемый входы CNOT два фотона, соответственно, в следующих состояниях: 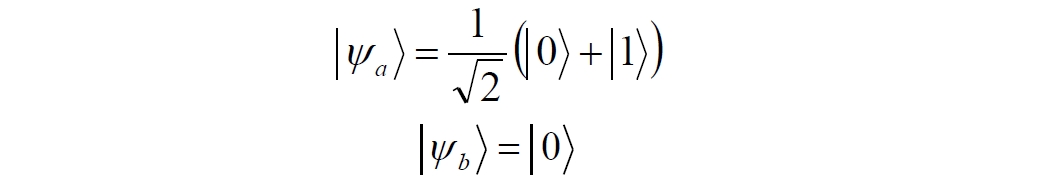 Это состояние системы фотонов на входе гейта будет описываться уравнением и матрицей вида: 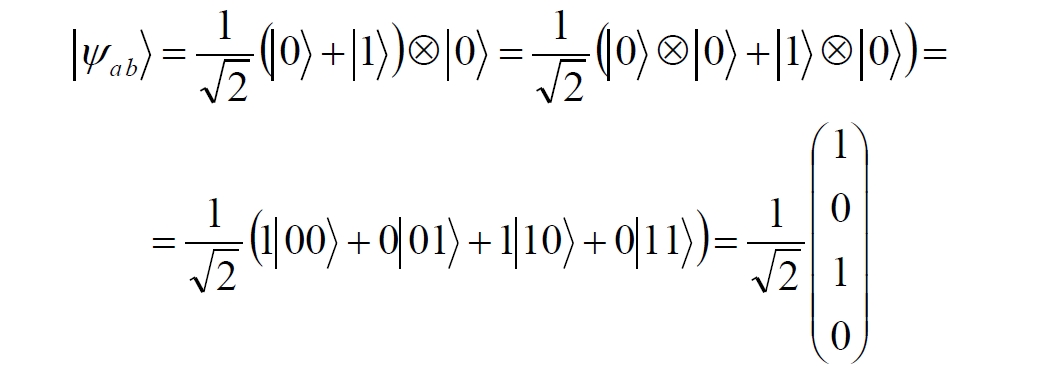 После прохождения фотонов через гейт будет получено новое состояние системы: 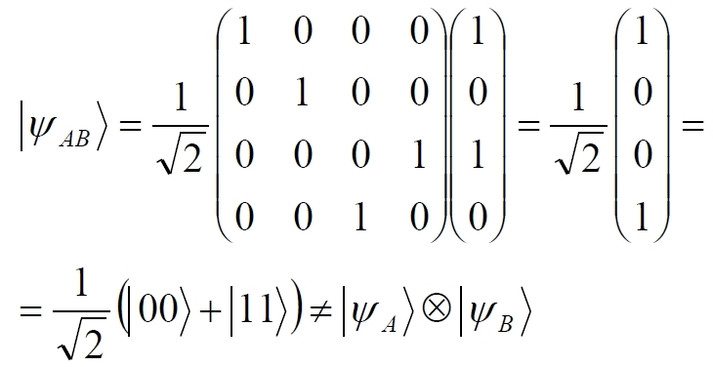 Знак неравенства означает, что на выходе получено запутанное (белловское) состояние фотонов: управляющего и управляемого, поскольку такое состояние не может быть факторизовано, то есть, не может быть представлено как тензорное произведение состояний независимых фотонов. Из этого сразу же следует, что входной управляющий сигнал на выход в неизменном виде все-таки не прошёл. Состояния квантовых частиц с нелокальными свойствами в квантовой механике известны как состояния полной запутанности - состояния Белла: 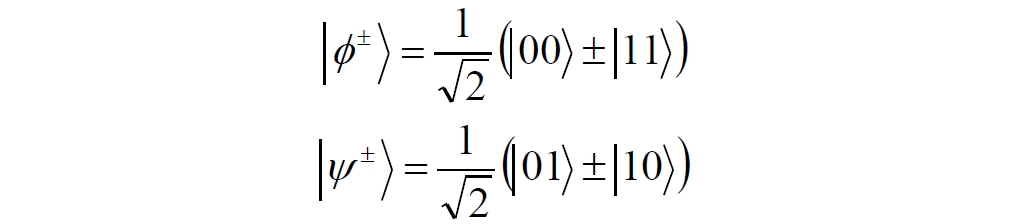 Два из этих состояний в литературе известны под собственными именами: ψ - - "ЭПР-состояние" и φ+ - "состояние шрёдингеровского кота". Частицы в состоянии запутанности ведут себя как единое целое независимо от расстояния между ними, демонстрируя полную и мгновенную взаимосвязь. Однако приведённые четыре состояния Белла - это лишь часть всех возможных состояний запутанности, их частный случай. Как и чистых состояний Белла, таких общих состояний также четыре: 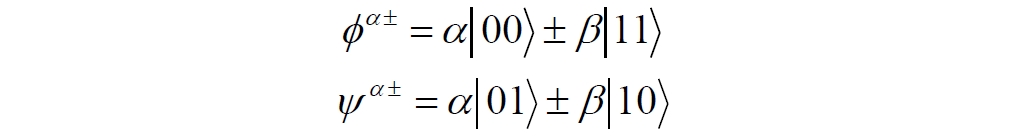 В литературе гейт CNOT описывается помимо уравнений также таблицей истинности, в которой, однако, не отражено это свойство гейта - создавать запутанные состояния. То есть, традиционная таблица истинности гейта CNOT неполна, и должна быть дополнена строками, отражающими создание запутанных состояний. В конец полной таблицы состояний гейта CNOT должны быть добавлены следующие две строки:  Эти строки показывают, что при определённых комбинациях входных сигналов на выходе образуется запутанное состояние, которое не является логическим сложением по модулю 2. Запутанные состояния приведены в общем виде, частным случаем которых являются запутанные состояния Белла φ± и ψ±, для которых α = β = 1/√2. Это дополнение расширяет понятие гейта "Controlled NOT" (CNOT, "управляемое НЕ"), поскольку его управляемый вход при определённых условиях становится управляющим. Телепортация запутанности Квантовая телепортация, то есть, мгновенная передача квантового состояния от одной частицы к другой - это свершившийся экспериментальный факт. В процессе традиционной "квантовой телепортации состояния" частицы (кубиты) преобразуются в специальной установке, где они последовательно изменяют свои состояния. Если немного видоизменить классическую установку, то можно попытаться осуществить еще одни вариант телепортации - "телепортацию состояния запутанности". Это более общий случай телепортации, когда телепортируется не состояние одного кубита, а состояние запутанности пары кубитов, что, вероятно, позволит получить новый интересный результат. Для такой расширенной телепортации в схеме традиционной установки следует поменять местами гейт CNOT и гейт Адамара, как показано на рис.2. 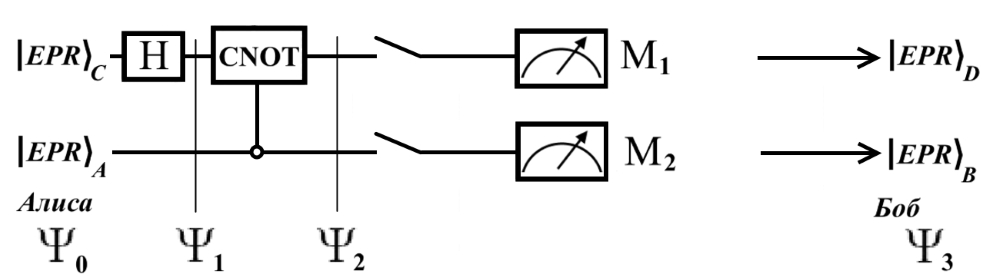 Рис.2. Установка для телепортации запутанности При описании процесса телепортации будем считать, что в его осуществлении принимают участие традиционные персонажи - Алиса и Боб. Пометим индексами A и C кубиты, принадлежащие Алисе, а индексами B и D кубиты, соответственно, принадлежащие Бобу. Волновые функции двух запутанных пар описываются уравнениями 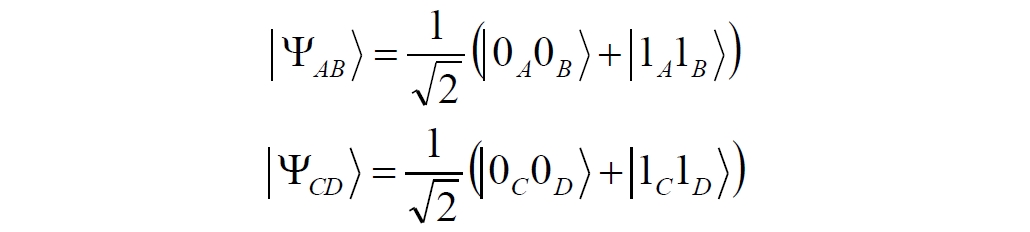 Тогда на стороне Алисы исходные, начальные состояния системы кубитов, участвующих в телепортации запутанности, можно записать следующим образом: 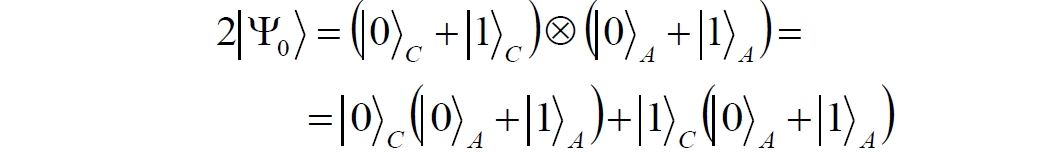 Здесь мы совершаем кажущееся нарушение формализма теории, поскольку фотоны Алисы запутаны с соответствующими фотонами Боба, поэтому, казалось бы, не могут быть описаны собственной волновой функцией. Однако при отсутствии воздействий на фотоны Боба для Алисы её фотоны ничем не отличаются от обычных, незапутанных фотонов, и она может работать с каждым из них как с обычным фотоном. В этом случае независимые фотоны Алисы описываются волновыми функциями: 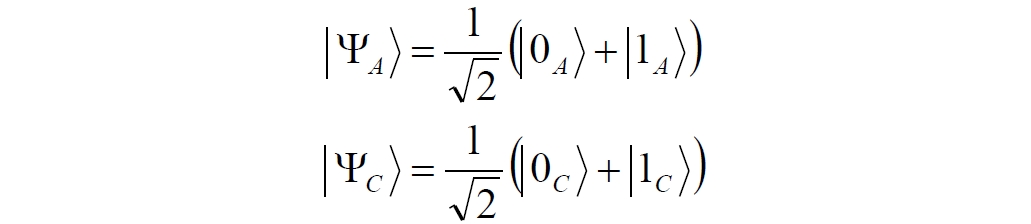 Пропустим кубит C Алисы через гейт Адамара. В результате получаем новую функцию системы 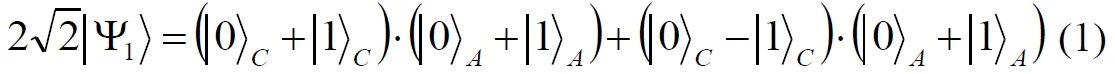 Раскрываем скобки у правых сомножителей 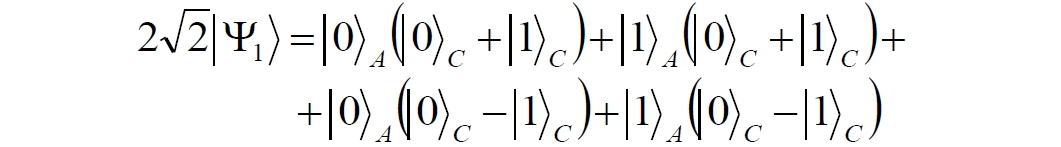 Раскрываем оставшиеся скобки и собираем однотипные члены уравнения 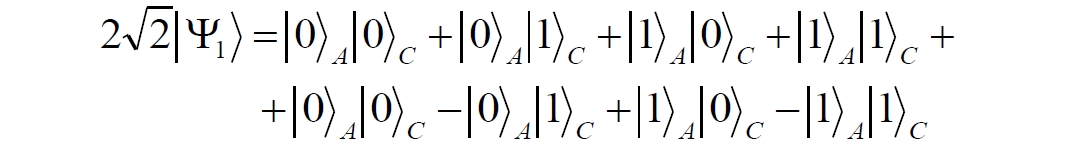 После группировки и сокращения получаем 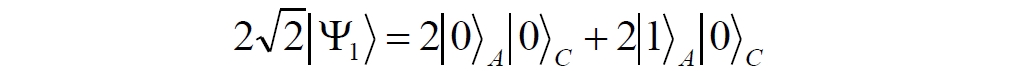 Здесь мы в рамках формализма квантовой информатики выполнили хотя и очевидные, но не вполне обоснованные математические операции: совпадающие члены уравнения мы сложили, а члены, имеющие противоположные знаки, сократили. Иначе запись должна была иметь вид: 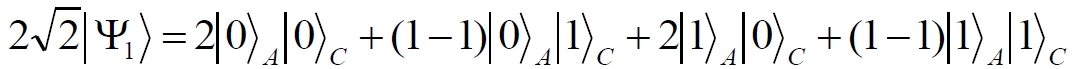 Но после сокращения получаем выражение 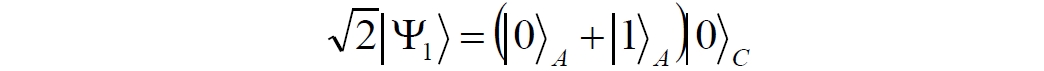 Заметим, что полученная волновая функции выглядит на первый взгляд довольно странно: 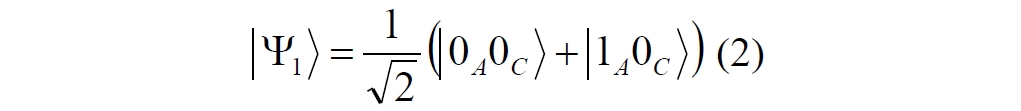 Это состояние не является запутанным, но любое совместное измерение всегда даст нулевую (горизонтальную) поляризацию фотона C. Казалось бы, фотоны независимы, поэтому любому результату измерения A должен соответствовать такой же любой результат измерения C. Но причиной образования состояния (2) является действие гейта Адамара: фотон C в результате попросту перешёл в пределах системы в ортогональное состояние |0С⟩. Пропустим полученную пару (2) через гейт CNOT. Для удобства перепишем новое состояние в матричном виде: 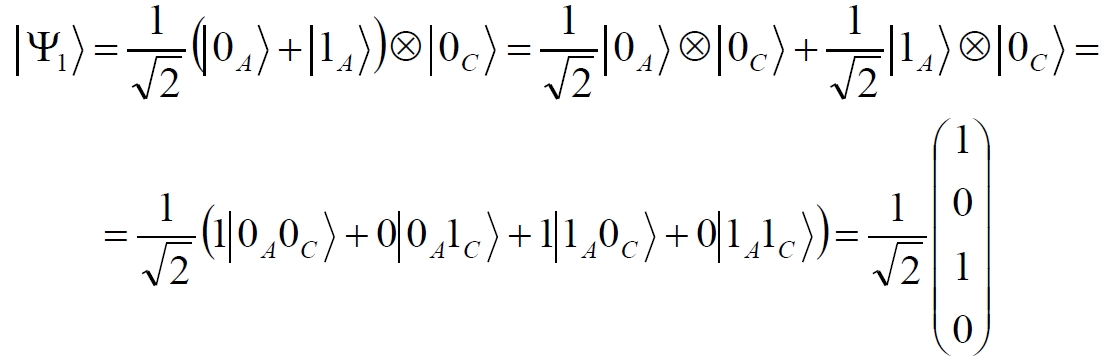 После прохождения фотонов Алисы через гейт CNOT состояние в матричном виде будет иметь вид: 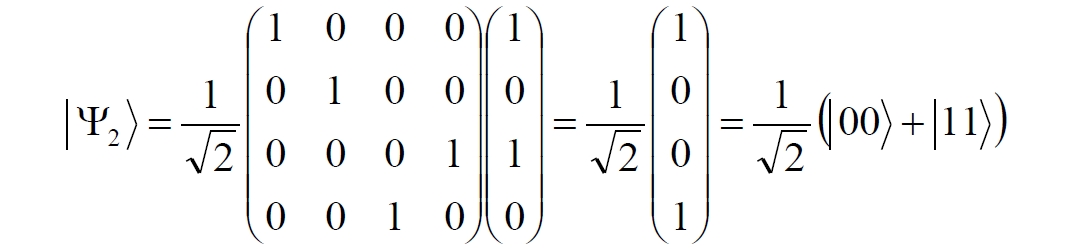 В дираковской форме волновая функция теперь уже не может быть представлена как тензорное произведение двух независимых волновых функций фотонов A и C, что означает запутанное состояние этих фотонов (чистое состояние Белла φ+, состояние шрёдингеровского кота): 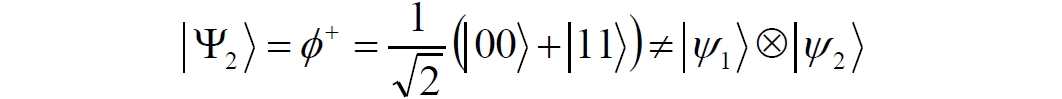 Для контроля проделаем все эти же преобразования в дираковской форме. Используем выражение (2): 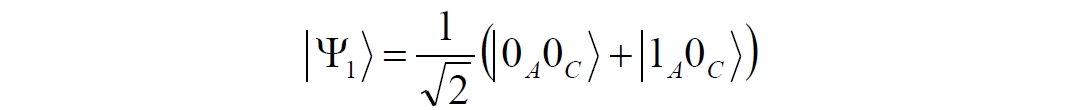 Пропустим эту пару через гейт CNOT и сразу же в соответствие с таблицей состояний гейта CNOT получаем то же самое новое состояние системы: 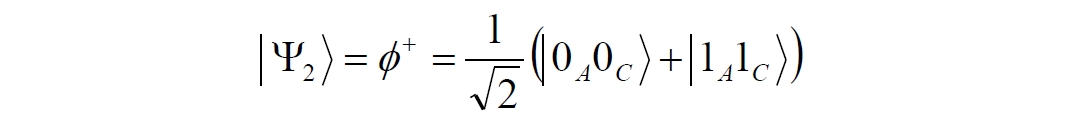 Итак, двумя способами мы получили один и тот же результат: на стороне Алисы фотоны A и C перешли в запутанное состояние. Однако каждый из этих фотонов запутан также и со своей исходной парой, поэтому вследствие унитарности проведенных преобразований неизбежно запутанными оказываются и фотоны, переданные Бобу: 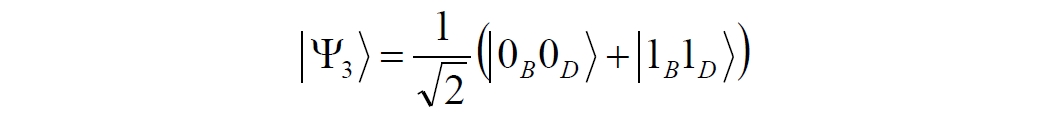 Если Алиса не делает над своими фотонами никаких измерений, то состояние запутанности сохранится и на стороне Боба. Это означает, что фотонам Боба передано запутанное состояние. В этом случае все измерения у Боба фотонов D и B будут давать 100% парных прохождений при любой ориентации поляризаторов. Если же Алиса произведёт измерение над любым из своих фотонов, то её фотоны перейдут в собственные состояния с разрушением запутанности, и точно так же запутанность разрушится и на стороне Боба. Теперь на стороне Боба при любом положении поляризаторов парных прохождений будет только 50%. Таким образом, Боб мгновенно узнает, что Алиса произвела измерение своих фотонов. Конечно, можно предположить, что на стороне Боба запутанность может иметь иной вид, поскольку на стороне Алисы фотоны были пропущены через гейт CNOT: 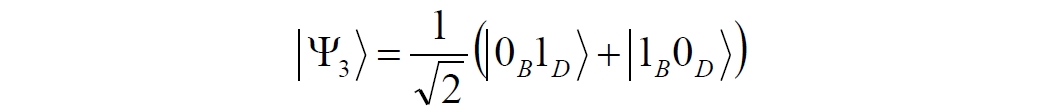 Однако это ничего не меняет по существу. Просто в этом случае парных прохождений не будет вообще, поэтому по-прежнему сохраняется возможность определить изменение состояний фотонов на стороне Алисы. Теперь уже возникает обратный эффект: при отсутствии измерений у Алисы на стороне Боба будут только равновероятные измерения |01⟩ и |10⟩. Напротив, при наличии измерений у Алисы на стороне Боба будут наблюдаться также и парные прохождения |00⟩ и |11⟩. Поскольку изменение состояния запутанности на пространственноподобном удалении является физически детектируемым, то это означает мгновенную, нелокальную, сверхсветовую передачу классической информации. Квантовый семафор Считается, что главной проблемой при использовании запутанности для передачи информации считается невозможность регистрации фактического состояния квантовых частиц и, как следствие, невозможность различения их неизвестных состояний. Еще одно ограничение на такое различение создаёт запрет на клонирование квантовых частиц: наличие копий частиц давало бы возможность множеством измерений определить их состояние, то есть, выявить различие между частицами, передаваемыми от передатчика к приёмнику. Таким образом, можно считать, что для принимающей стороны главной проблемой является проблема различимости, то есть, возможности различить посылаемые передатчиком сигналы, квантовые состояния. Передатчик изменяет состояния своих частиц, что приводит к изменению состояния удалённых, принимаемых приёмником частиц, то есть передаёт им квантовую информацию. Считается твердо установленным, что приёмник не способен различить квантовые частицы по их изменённым состояниям, не способен непосредственно "прочитать" эти изменения квантового состояния частицы, превратив их в классическую, читаемую информацию. Рассмотрим возможности гейта CNOT для использования в режиме фильтрации, селекции фотонов в различных состояниях - их различения. Этот гейт, как отмечено выше, осуществляет логическое сложение сигналов по модулю 2, причём считается, что сигнал на управляющем выходе равен сигналу на управляющем выходе просто вследствие того, что это одна и та же линия (a = A). Однако это справедливо только для ортогональных состояний управляющего кубита. Управляющий кубит в произвольном состоянии будет запутан с управляемым кубитом, потеряет своё первоначальное состояние и перейдет в состояние запутанности. Таким образом, гейт CNOT оказывается чувствительным к направлениям поляризации как управляемого, так и управляющего фотонов, и это, вероятно, может позволить приёмнику явно зарегистрировать эти направления. Для определенности назовем "несущей" нелокальную связь фотонов, передающую квантовую информацию. В качестве несущей передаваемой информации удобнее всего использовать чистое запутанное состояние Белла φ+, состояние шрёдингеровского кота: 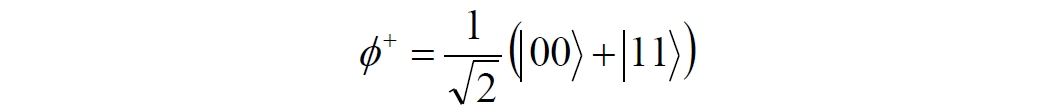 Соответственно, изменение угла наклона поляризатора у передатчика при измерении собственных фотонов из запутанных пар можно назвать фазовой модуляцией нелокальной несущей. При такой модуляции на стороне приёмника также происходит изменение угла наклона поляризации фотонов. Вот эту фазовую составляющую нелокальной несущей на стороне приёмника и позволяет выделить квантовый гейт CNOT. В основу модуляции положено следующее явление. Логический анализ явления запутанности с точки зрения квантовой теории приводит к выводу, что опережающее измерение запутанных фотонов в одном канале, в передатчике приводит к созданию во втором канале, в приемнике двух смешанных плоско-поляризованных потоков с взаимно перпендикулярными поляризациями. Собственно эффект модуляции несущей состоит в изменении их угла поляризации. На рис.3 приведена простейшая схема эксперимента по проверке квантовой корреляции, демонстрирующая механизм модуляции нелокальной несущей. Источник S испускает пару запутанных фотонов v1 и v2, которые встречают на своем пути два поляризатора I и II, расположенные перпендикулярно, то есть с взаимным углом, равным π/2. На рисунке фотон v1 не показан, поскольку считаем, что он уже был измерен своим поляризатором I. После коллапса волновой функции фотоном v1 на поляризаторе I второй фотон v2 приобретает одну из двух возможных поляризаций: параллельную или перпендикулярную к направлению модулирующего поляризатора I.  Рис.3. Образование крестовой поляризации Воспользуемся квантово-механической формулой, дающей вероятность прохождения фотона через поляризатор, если угол между поляризаторами равен θ: 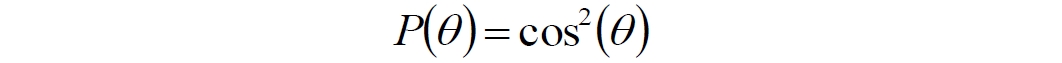 Очевидно, в рассматриваемом случае совместных прохождений фотонов не будет: 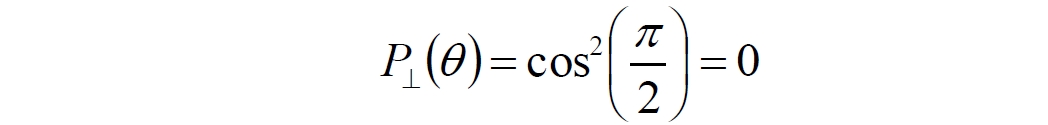 Однако через каждый из поляризаторов некоторые фотоны пройдут. Наблюдатели, находящиеся рядом с поляризаторами, зафиксируют вероятность прохождения фотонов, равную 1\2. Если источник испустит, например, 1000 фотонов, то через каждый из поляризаторов пройдут ровно половина - 500 фотонов. Но это будут некоррелированные фотоны: среди пар не будет ни одной, в которой один из фотонов прошёл через поляризатор одновременно со вторым фотоном, прошедшим через другой поляризатор. Наоборот, если поляризаторы параллельны, то есть угол θ между ними равен нулю, то через поляризаторы будут проходить только парные фотоны: если пройдет первый фотон, то второй будет спроектирован в коллинеарную поляризацию и так же пройдет через свой поляризатор с вероятностью 1. Предположим, что первый поляризатор находится вплотную к источнику S, а второй - на некотором удалении. Поэтому фотоны в направлении влево будут измерены сразу же при вылете из источника. Если этот фотон пройдет через свой поляризатор, то в этот же момент их парные фотоны приобретут поляризацию, параллельную, коллинеарную первому поляризатору. Это означает, что выходной поток в сторону второго поляризатора будет состоять словно бы из двух фотонных потоков. Первый из этих потоков - это поток плоско поляризованных фотонов с известным направлением поляризации - параллельной первому поляризатору. Будет и второй поток - из фотонов, которые имеют другое направление поляризации. Попробуем выяснить, какое именно. Установим на пути потока фотонов поляризатор II, параллельный первому. Очевидно, что известный нам поток из плоско поляризованных фотонов пройдет через поляризатор с достоверностью. Известно также, что это ровно 1\2 от общего числа всех фотонов, испущенных источником в данном направлении. Исследователь на этой стороне зафиксирует этот факт. Но он может не знать, что фотоны в потоке имеют определенные направления поляризации и скажет, что через поляризатор проходят 1\2 от всех фотонов в потоке. Он (исследователь) не разделяет этот поток на два и считает, что через поляризатор с вероятностью 1\2 проходит любой из прилетевших фотонов. Но мы знаем, что в общем потоке имеется известный нам подпоток, который пройдет через поляризатор с вероятностью 1, и их общее количество равно тому количеству, которое зафиксирует исследователь. Следовательно, остальные фотоны не пройдут через поляризатор, а будут задержаны с вероятностью 1. То есть из остальных фотонов через поляризатор не пройдет ни один. Это означает, что средняя вероятность фотонов в остальном потоке равна 0. Поэтому мы можем с уверенностью сказать, что весь этот поток состоит из плоско поляризованных фотонов с поляризацией, перпендикулярной направлению нашего поляризатора (и, соответственно, первого поляризатора), поскольку через поляризатор с достоверностью не проходят только перпендикулярно поляризованные фотоны. Это обстоятельство не должно вызвать особых возражений и вполне объяснимо. Фотоны, которые не прошли через первый поляризатор, коллапсировали, очевидно, получив направление поляризации, перпендикулярное первому поляризатору и были им поглощены. Парный им фотон автоматически был спроектирован в такое же направление поляризации и тоже был поглощен вторым поляризатором. Итак, мы можем с достаточной уверенностью заявить, что в рассматриваемой схеме эксперимента по второму направлению, вправо излучаются два потока плоско поляризованных фотонов: с вертикальной и с горизонтальной поляризацией (относительно первого поляризатора). Это обстоятельство не противоречит математике квантовой теории. Понятно, что эти потоки представляют собой случайную смесь, в которой фотоны с ортогональными поляризациями встречаются в случайной последовательности. Эту смесь из ортогонально поляризованных фотонов можно вращать, наклоняя поляризатор I вблизи передатчика. В простейшем случае мы можем выбрать два фиксированных направления, когда потоки вертикально-горизонтальные и имеют наклоны ±45 градусов к горизонтали. Это максимально возможные градации углов. Пусть для передачи информации передатчик на своей стороне измеряет фотоны из запутанных пар одним из этих положений: вертикальным или наклонённым под 45о поляризатором. В этом случае на стороне приёмника фотоны также образуют два разных сигнала, каждый из которых состоит из двух таких же ортогональных поляризованных потоков в виде вертикального и наклонного под 45о "крестов". Следовательно, измерений на стороне приемника должно быть, по меньшей мере, четыре, поскольку он принимает четыре различно поляризованных фотона: вертикально, горизонтально, под углом +45о и под углом -45о. Главная цель приёмника - различить эти два ортогонально поляризованных потока-креста. Попробуем выяснить, возможно ли это. Произведём измерения четырёх возможных состояний с помощью одной и той же схемы. Передача сигнала нуля Сначала рассмотрим смесь из двух потоков ортогонально поляризованных фотонов: с вертикальной и горизонтальной поляризацией, вертикальный "крест". Попробуем использовать его для передачи сигнала "ноль", "нет", false, точка азбуки Морзе и так далее. Каждый из фотонов этой смеси имеет либо вертикальную поляризацию, либо горизонтальную. Пропустим эту смесь через гейт CNOT: поток поступает на управляющий вход гейта, а на управляемый вход подадим фотоны с горизонтальной поляризацией. С выходов гейта CNOT фотоны подаются на два соответствующих наклонённых на 45 градусов расщепляющих поляризатора с ± выходами (П1 и П2 на рис.4). Произведем измерения фотонов этого потока. Измерение вертикальной составляющей потока прямого "креста". Для вертикально поляризованного потока на входе гейта имеем входное двухкубитное состояние: 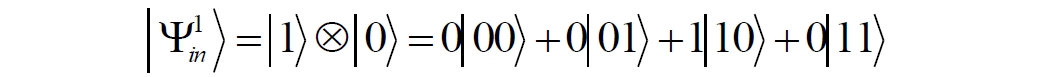 Этот вектор в матричном виде, в виде столбца коэффициентов запишем в следующем виде: 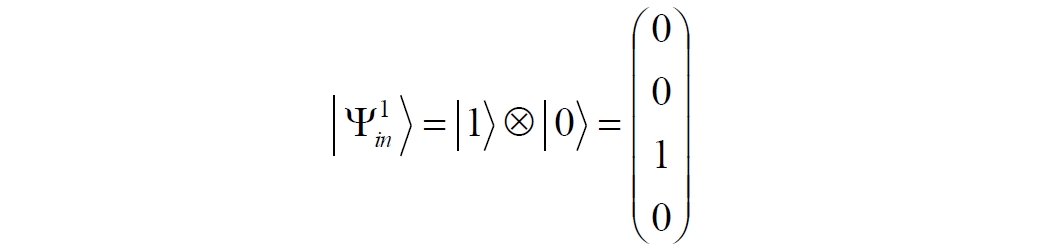 Следовательно, после прохождения через гейт CNOT волновая функция в матричном виде будет преобразована следующим образом: 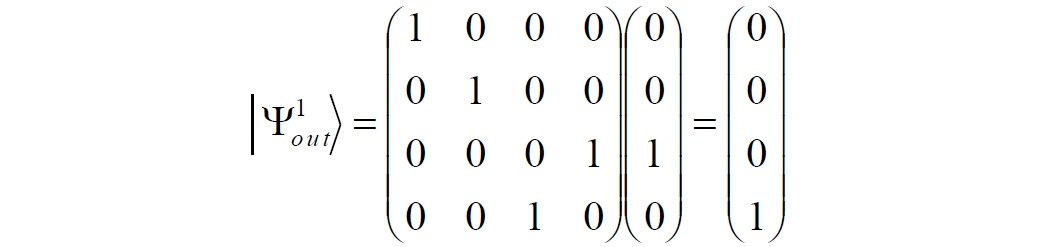 В дираковской форме эта волновая функция может быть представлена как тензорное произведение двух независимых волновых функций, то есть, пара не является запутанной: 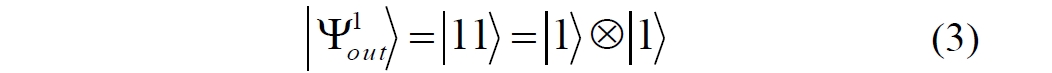 Эти два фотона (из потока и управляемый фотон на выходе) поступают на два наклонённых под 45 градусов расщепляющих поляризатора, каждый из фотонов - через свой поляризатор. Поскольку фотоны независимые, то через эти одинаково ориентированные поляризаторы на одноименные выходы пройдёт по 50% фотонов с управляющего и управляемого выходов гейта CNOT. Вероятность парного прохождения, то есть, когда на одноименные выходы разных поляризаторов пройдут оба фотона пары, согласно закону Малуса будет равна: 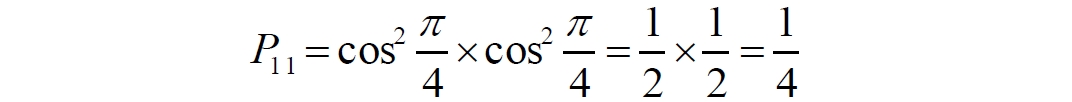 Это очевидно, поскольку в базисе поляризаторов фотоны описываются одинаковыми волновыми функциями 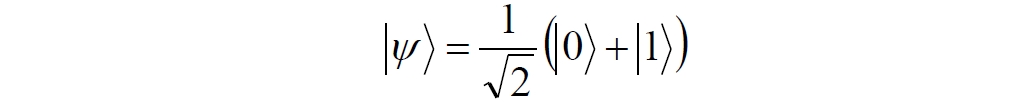 Таким образом, поскольку фотоны не запутанные, совпадений при прохождении через поляризаторы будет 50% (25% - оба прошли на плюс, 25% - оба прошли на минус). Измерение горизонтальной составляющей потока прямого "креста". Для горизонтально поляризованного фотона на управляющем входе гейта CNOT и горизонтально поляризованного фотона на управляемом входе имеем волновую функцию: 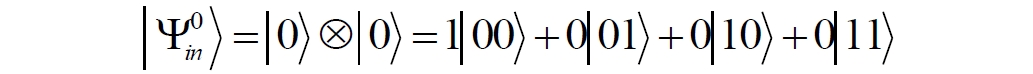 Или в матричном виде: 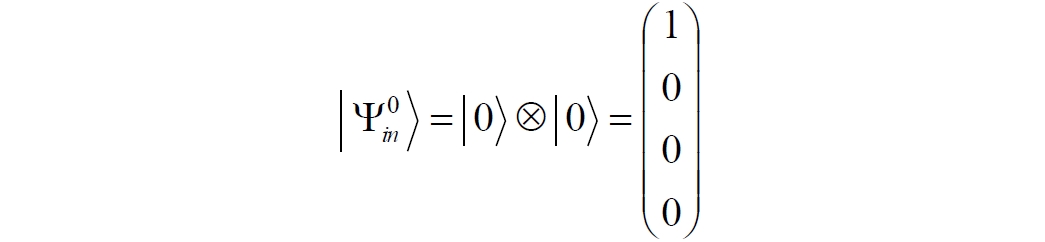 На выходе CNOT получаем функцию в матричном виде: 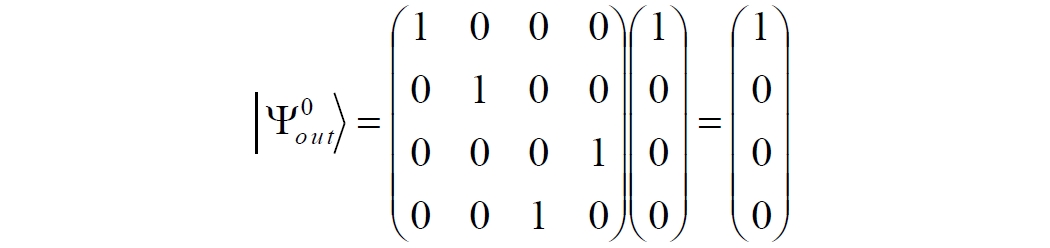 В дираковской форме эта волновая функция также может быть представлена в виде тензорного произведения двух независимых волновых функций, то есть, пара так же не является запутанной: 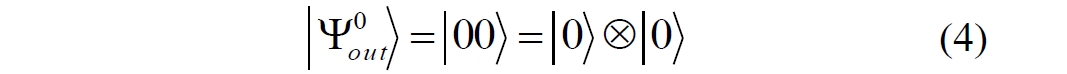 Поскольку фотоны на управляющем и управляемом выходах гейта CNOT независимые, то при их прохождении через наклонённые на 45 градусов поляризаторы также будет по 25% совпадений. Волновые функции фотонов будут иметь вид 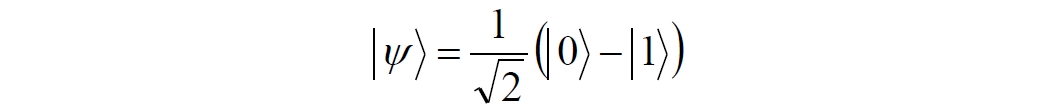 Вероятность парного прохождения, то есть, когда через одноименные выходы поляризаторов пройдут оба фотона, как и в предыдущем случае, будет равна: 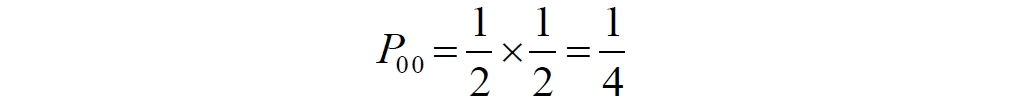 То есть, и в этом случае совпадений при прохождении через поляризаторы будет 50% (25% - оба прошли на плюсовые выходы, 25% - оба прошли на минусовые выходы). Но каждый из полу-потоков составляет 50% от общего количества фотонов в потоке, поэтому в их полном количестве парные совпадения также будут равны, соответственно, P00 и P11. То есть, хотя в каждом полу-потоке вероятность парного прохождения равна 50%, в полном потоке это количество составит только 25%. Следовательно, общее совместное одноименное прохождение, таким образом, составит 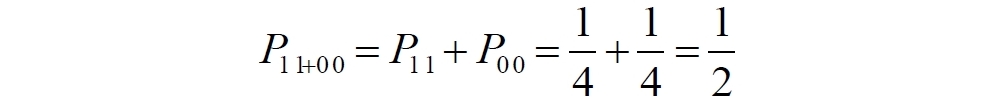 Такое 50-процентное совпадение обозначим как сигнал "ноль", "нет", false, точка азбуки Морзе и так далее. Передача сигнала единицы В случае поворота поляризатора передатчика на вход приемника поступят два ортогонально поляризованных потока фотонов с наклоненной на 45 градусов вертикальной и горизонтальной поляризацией (наклонный "крест"). Попробуем использовать его для передачи сигнала "единица", "да", true, тире азбуки Морзе и так далее. Смесь в этом случае будет содержать два потока фотонов с волновыми функциями: 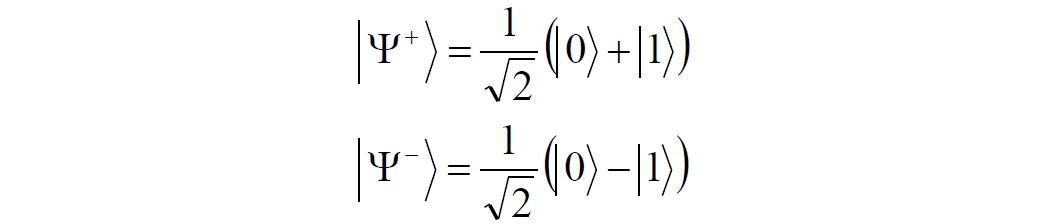 Измерение составляющей Ψ+ потока наклонного "креста". Для этой составляющей на управляющем входе гейта CNOT и горизонтально поляризованного фотона на его управляемом входе имеем волновую функцию и её матричную форму: 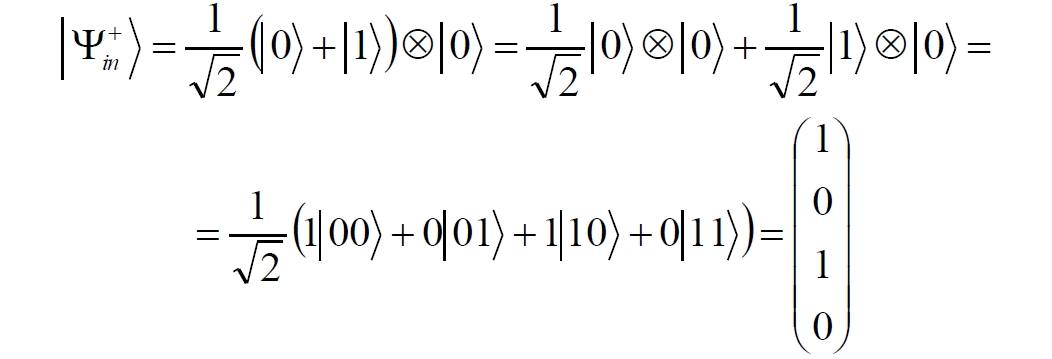 После их прохождения через гейт получим состояние в матричном виде: 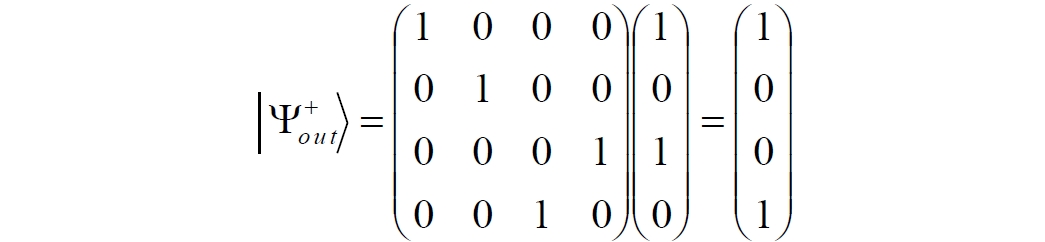 В дираковской форме волновая функция теперь уже не может быть представлена как тензорное произведение двух независимых волновых функций, что означает запутанное состояние фотонов (чистое состояние Белла φ +, состояние шрёдингеровского кота): 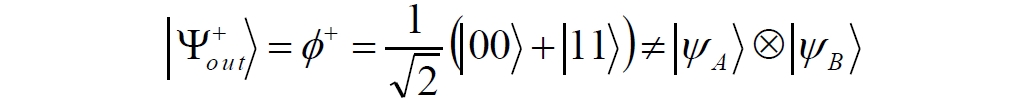 Поскольку фотоны запутанные, то при их прохождении через наклонённые на 45 градусов поляризаторы оба всегда с единичной достоверностью пройдут на одноименные выходы. И на плюсовой и на минусовой выходы фотоны пройдут одновременно с вероятностью: 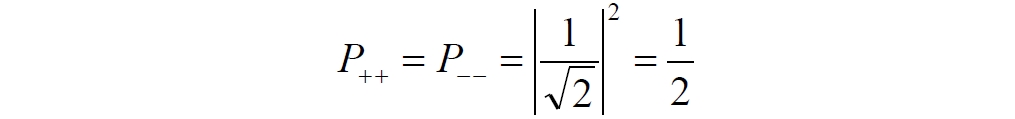 Вероятности разноименных прохождений равны нулю: 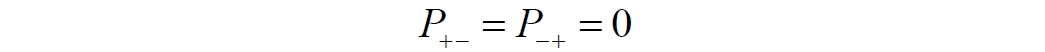 Таким образом, совпадений при прохождении через поляризатор будет 100% (50% - оба прошли на плюсовой выход, 50% - оба прошли на минусовой выход): 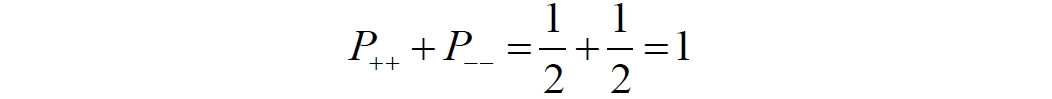 По количеству фотонов это составит 50 фотонов из 100 для каждого из совпадений для данного полу-потока или из 200 пар фотонов в полном потоке. Измерение составляющей Ψ- потока наклонного "креста". Для этой составляющей потока на управляющем входе гейта и горизонтально поляризованного фотона на управляемом входе гейта имеем волновую функцию и её матричную форму: 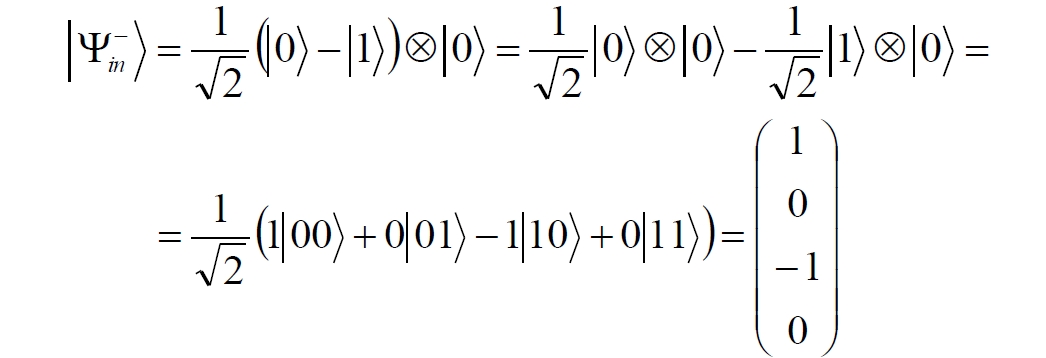 После их прохождения через гейт CNOT получим совместное состояние в матричном виде: 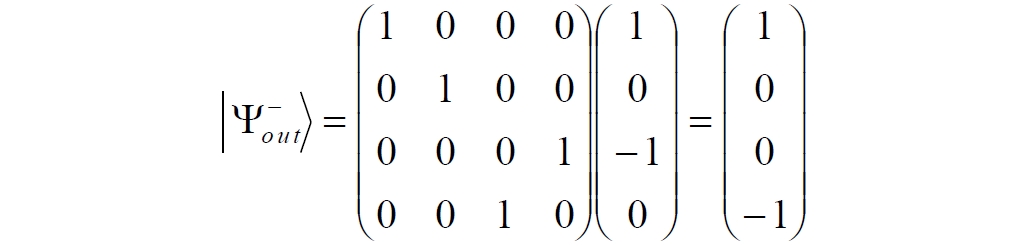 И в этом случае в дираковской форме волновая функция не может быть представлена как тензорное произведение двух независимых волновых функций, что означает запутанное состояние фотонов (чистое состояние Белла φ-). Эта волновая функция имеет следующий вид: 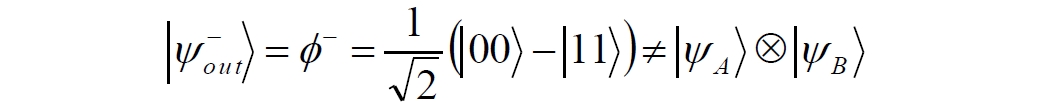 Поскольку фотоны запутанные, то через наклонённые на 45 градусов поляризаторы, как и в предыдущем случае, пройдёт 50% пар управляющих и управляемых фотонов с выхода гейта CNOT. То есть, на одноименные выходы расщепляющих поляризаторов оба фотона пройдут с вероятностью: 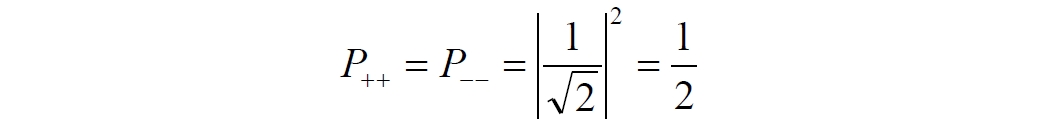 По количеству фотонов это вновь составит 50 фотонов из 100 для каждого из совпадений. Вероятности разноименных прохождений в этом случае также равны нулю: 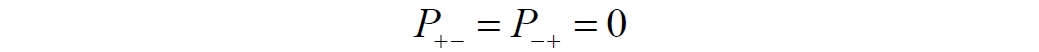 Таким образом, как и в предыдущем случае, совпадений при прохождении через поляризатор будет 100%, (50% - оба прошли на плюсовый выход, 50% - оба прошли на минусовый выход), то есть, для суммарного прохождения фотонов двух полу-потоков эта величина составит 200 фотонов из 200: 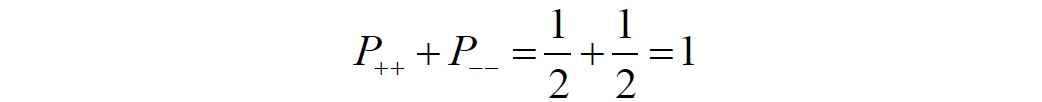 Такое 100-процентное совпадение, то есть парное прохождение всех фотонов, то есть, 200 фотонов из 200 в приведенных числовых примерах, мы обозначим как сигнал "единица", "да", true, тире азбуки Морзе и так далее. Как видим, передатчик формирует два отчетливо различимых для приёмника потока. Первое и второе измерения, вертикальный крест дают в приёмнике количество совпадений (50%), надёжно отличающееся от количества совпадений, которое дают третье и четвёртое измерения (100%), наклонный крест. Состояния фотонов на стороне передатчика формируются, например, поворотом рукоятки поляризатора - в вертикальное или наклонное положение. Фотонам на стороне приёмника эти состояния передаются со сверхсветовой (нелокальной) скоростью. Квантовый гейт CNOT позволяет различить эти модулированные состояния запутанных фотонов, определить в каком положении на стороне передатчика находилась рукоятка поворотного поляризатора. 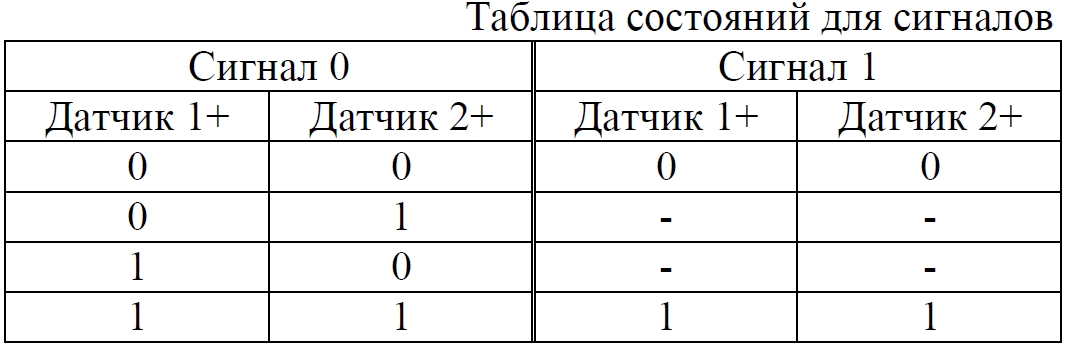 Обобщенно результаты измерений можно свести в две таблицы состояний: для сигналов 1 и для сигналов 0. Поскольку возможны 4 комбинации сигналов на выходах измерителей, для нижнего уровня достоверности должно производиться измерение как минимум 4-х последовательных фотонов. Согласно колонкам Сигнал 0 обязательно будут зафиксированы противофазные фотоны. Другими словами, наличие противофазных фотонов (разноименных совпадений) означает получение приемником сигнала 0. Очевидно, что и передатчик и приемник можно легко автоматизировать, использовать компьютерную технику. Наиболее сложным является формирование несущей, то есть создание и разделение фотонных пар между передатчиком и приемником, создание своеобразного подобия телеграфных проводов. Но здесь возникает серьезный вопрос: каким же образом неуловимая, неощутимая квантовая информация вдруг позволила все-таки передать информацию классическую, вещественную? Вероятно, что в данном случае, по всей видимости, удалось обойти запрет на клонирование фотона. Хотя о единственном случае клонирования было известно и ранее: это клонирование фотона в базисном состоянии. Такое клонирование осуществляет гейт CNOT. Эта одна-единственная, буквально крошечная возможность создания клонированного фотона допустила возможность передачи классической информации, формально даже и не нарушая теорему о запрете клонирования кубита. Опишем такую возможность передачи информации в виде небольшой истории с традиционными участниками Алисой и Бобом, которые решили осуществить передачу сигналов посредством квантового нелокального семафора. Почему семафор, а не традиционные телепортация или телеграф? Дело в том, что два ортогональных сигнала - вертикальный и наклонный кресты поляризованных фотонов довольно сильно напоминают морской семафор, когда матрос размахивает флажками, образуя разные фигуры. Очевидно, что разница наклонов в 45 градусов соответствует максимальной различимости положения таких крестов. Конечно, в этом случае используется не морская семафорная азбука, а азбука Морзе, поскольку у таких флажков только два положения, хотя возможно и сколь угодно много промежуточных положений. Итак, для такого эксперимента они собрали модель квантового нелокального семафора примерно такого вида, как показано на рис.4. На одинаковом расстоянии от себя они установили источник запутанных фотонов S, который испускает непрерывную последовательность фотонных пар v1 и v2. Свои полученные фотоны Алиса пропускает через вращаемый поляризатор. Чтобы передать Бобу сообщение с помощью азбуки Морзе, Алиса поворачивает свой поляризатор в одно из двух положений. Вертикальное положение поляризатора означает точку (ноль), наклонное под 45 градусов - тире (единицу). На своей стороне Боб принимает вторые из пар запутанные фотоны и пропускает их через квантовый гейт CNOT, подавая на его управляющий вход полученные запутанные фотоны, а на управляемый вход - фотоны с горизонтальной поляризацией. 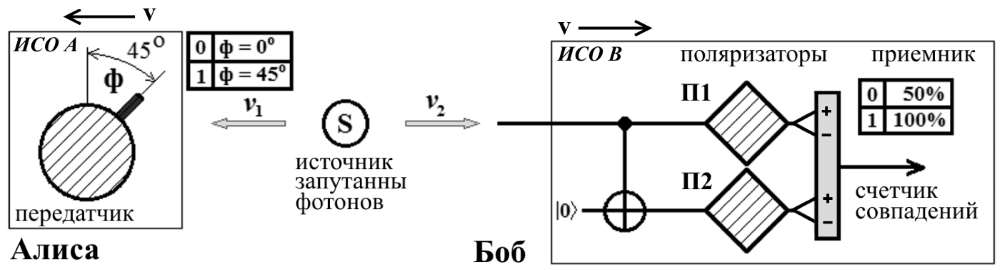 Рис.4. Квантовый нелокальный семафор С выхода гейта управляющий и управляемый фотоны Боб пропускает через наклоненные под 45 градусов расщепляющие поляризаторы и с помощью устройства совпадения измеряет парные регистрации, когда оба фотона одновременно прошли либо на одноименные их выходы (плюсовые или минусовые), либо на разноименные. Конечно, использование расщепляющих поляризаторов не обязательно, поскольку всякое прохождение на один выход тождественно отсутствию такого прохождения на другой. Устройство совпадения выдаёт информацию о процентном соотношении парных регистраций. Если все фотоны парно прошли через одноименные выходы поляризаторов (100%-ное совпадение), то Боб записывает тире (единицу). Если одноименных регистраций только 50%, то Боб записывает точку (ноль). Поскольку совпадения формируются при коллапсе волновых функций запутанных фотонов v1 и v2, то такая передача текста азбукой Морзе происходит со сверхсветовой скоростью [7, 6]. Заключение В заключение следует сделать, видимо, неожиданный вывод. Остаются сомнения в окончательном и убедительном доказательстве того, что квантовая нелокальность может быть использована для сверхсветовой передачи информации - слишком уж много вопросов возникает в физике при такой возможности. Но, если приведённые выкладки неверны, то в чём ошибка? Возможно, она заключена в трактовке запутанности. В частности, видимо, только эксперимент может подтвердить, что при запутывании пар запутанных фотонов на одной стороне приведёт к запутанности и их удалённых пар. Кроме того, если посмотреть литературу по CNOT, то можно встретить утверждения, что на выходе гейта фотоны запутаны всегда и во всех режимах. В этом случае селекция фотонов на выходах предложенной схемы не позволит различить их исходное состояние и передачи информации не будет. Другими словами, уравнения (3) и (4) тоже, видимо, представляют запутанные состояния фотонов, хотя это довольно странные состояния запутанности. Действительно, в этом случае оба фотона находятся в собственных состояниях и имеют точно определённые поляризации, а их совместное состояние является тензорным произведением, означающим отсутствие запутанности, вопреки многочисленным заявлениям от имени квантовой механики! Такая запутанность, если она действительно имеет место, весьма красочна. Фотон с достоверно известной поляризацией без какого бы то ни было влияния извне поворачивает её в приемнике на глазах экспериментатора. И сразу же становится очевидным, что такая запутанность с ещё большей простотой позволяет произвести сверхсветовую передачу информации. Поворачивая поляризатор у фотона в передатчике, мы получаем на выходе такое же вращение фотона в приемнике. В любом случае рассмотренная семафорная квантовая сигнализация, "странная запутанность" или управляемое переключение состояния запутанности пары удалённых фотонов фактически создают ряд серьёзных физических проблем, парадоксов. Появляется возможность сверхсветовой передачи классической информации, что де-факто вступает в противоречие со специальной теорией относительности. Прямо говоря, опровергает её основные положения. Становится недействительным вывод из основного постулата теории - о предельности скорости света и невозможности сверхсветовой передачи взаимодействия или сигналов. Отвергаются принцип относительности одновременности, преобразования Лоренца. Конечно, такую сигнализацию довольно сложно использовать в дальней космической связи, хотя это было бы самым перспективным её приложением. Для такой связи требуется создать некое фотонное подобие обычной телеграфной линии связи (провода, оптоволокно), что связано с заметными техническими трудностями. Но её достаточно просто использовать для кодированной передачи информации. Источник запутанных фотонов передает их отправителю и получателю, например, по обычной волоконно-оптической линии, либо со спутника. Передача информации производится либо непосредственно путем описанной семафорной сигнализации, либо передачей открытого ключа. Любое постороннее вмешательство в сеанс связи сразу же обнаруживается по нарушению контрольных сумм и может быть незамедлительно пресечено. Очевидно, что две рассмотренные выше ИСО Алисы и Боба, связанные таким каналом связи, могут двигаться относительно друг друга с любой скоростью, что, собственно, и ведёт к возникновению сверхсветовых парадоксов теории относительности. Как известно, сверхсветовую сигнализацию теория относительности нередко трактует как сигнализацию во времени, как передачу информации в прошлое, то есть, как некий вариант машины времени. Однако это неверный подход. Сверхсветовая сигнализация опровергает основы специальной теории относительности, поэтому и все её выводы в этом случае также становятся недействительными. Библиографические ссылки: 1. Bell J.S., On the Einstein Podolsky Rosen paradox, Physics Vol.1, No.3, pp.198-200, 1964 2. Walleczek J., Groessing G., Nonlocal quantum information transfer without superluminal signalling and communication, arXiv:1501.07177v3 [quant-ph] 3. Доронин С.И., "Не локальность квантовой механики", форум на сайте "Физика магии", URL (недоступен): http://physmag.h1.ru/forum/topic.php?forum=1&topic=29 Эйнштейн А. Собрание научных трудов в четырех томах. Том 4. Статьи, рецензии, письма. Эволюция физики. М.: Наука, 1967 5. Эйнштейн А., Подольский Б., Розен Н. Можно ли считать квантовомеханическое описание физической реальности полным? / Эйнштейн А. Собр. научных трудов, т.3. - M.: Наука, 1966, с. 604-611 6. Дополнения к статье, сайт Самиздат, URL: http://samlib.ru/p/putenihin_p_w/teledop.shtml 7. Путенихин П.В., Нелокальная квантовая передача классической информации, журнал "Точная наука", ИД "Плутон", вып.33 от 17 декабря 2018 г., URL: https://elibrary.ru/item.asp?id=36746320 | |
| Категория: Разное | | | |
| Просмотров: 1755 | Загрузок: 533 | |
| Всего комментариев: 0 | |