Путенихин П.В. Как распутать квантовую запутанность
| 20.05.2021, 19:58 | |
Люди верят в чудеса и любят их. Хотя и говорят, что чудес на свете не бывает, но они порой обнаруживаются там, где их, уж, никак не ожидаешь – в физике. Одной из важнейший обязанностей любой физической теории является предсказание новых явлений, которые не были известны до создания этой теории. Такие предсказания, подтвержденные впоследствии экспериментами, являются наиболее убедительным доказательством истинности теории, её права на существование. Самым превосходным образом эту свою обязанность исполняет квантовая механика. Среди множества предсказанных ею явлений есть невероятные, удивительные явления, смысл которых воспринимается с трудом. Одним из самых удивительных таких предсказаний квантовой механики является «запутанность». На её основе впоследствии было сделано ещё одно, пожалуй, более широко известное предсказание: телепортация. Не вымышленная телепортация из фантастических рассказов, а реальное физическое явление. Википедия явлению квантовой запутанности дает такое описание: «Квантовая сцепленность (англ. entanglement «запу́танность, спу́танность, перепу́танность») — квантовомеханическое явление, при котором квантовое состояние двух или большего числа объектов должно описываться во взаимосвязи друг с другом, даже если отдельные объекты разнесены в пространстве. Вследствие этого возникают корреляции между наблюдаемыми физическими свойствами объектов. Например, можно приготовить две частицы, находящиеся в едином квантовом состоянии так, что когда одна частица наблюдается в состоянии со спином, направленным вверх, то спин другой оказывается направленным вниз, и наоборот, и это несмотря на то, что согласно квантовой механике, предсказать, какие фактически каждый раз получатся направления, невозможно. Иными словами, измерения, проводимые над одной системой, оказывают мгновенное воздействие на сцепленную с ней. Однако то, что понимается под информацией в классическом смысле, не может быть передано через сцепленность из-за статистического характера передаваемой информации». Это достаточно полное описание. Однако в нём не видно того, что квантовая запутанность является парадоксальным, прямо-таки мистическим явлением. Само по себе как физическое явление оно не вызывает никаких особых вопросов. Непривычное, даже забавное название, не более того. Но в современной физике таких забавных названий и терминов - хоть отбавляй. Как и явлений, понять которые непросто даже в описательном смысле. Не в глубоком физическом, не взглядом профессионала, а в образном смысле, как же это выглядит, как это проявляется. Приведём такой образный пример. Фраза «односторонняя монета» может звучать забавно и странно. Сразу же возникают различные ассоциации, требующие пояснений: - Наверное у монеты обе стороны одинаковые? - Нет! У монеты только одна сторона! - Может быть монета имеет шарообразную форму? - Нет! Это обычная плоская монета. - Тогда она, видимо, имеет форму ленты Мёбиуса? - Нет же! Это самая обычная монета! - Какая обычная? Круглая? Вроде пятака? - Да, именно! - И у этого круглого пятака только одна сторона?! - Да, именно так. - Но этого же не может быть! Примерно в так можно сказать и про явление запутанности: этого не может быть. Опишем его подробнее. Для этого рассмотрим упрощённую, схематичную модель. Допустим, у нас есть два фотона - квантовые частицы. Для простоты представим их в виде двух одинаковых монет [14]. Скажем, однокопеечных. Назовём «решку» этих монет «спином» (направлением спина в сторону решки).  Рис.1 Слева монета, изображающая первый фотон, лежит «спином вверх», справа монета, изображающая второй фотон, лежит «спином вниз» в результате 12-го подбрасывания монет. Если монета лежит решкой вверх, то это означает, что у фотона (который эта монета олицетворяет) спин, соответственно, тоже направлен вверх. Далее неким хитрым способом «запутаем» эти два фотона. Для монет это будет, предположим, их совместное встряхивание в стакане. Для реальных фотонов этот процесс связан с их совместным испусканием, например, специально обработанным кристаллом. Теперь у нас есть две «запутанные» (сцепленные, перепутанные) монеты (два фотона в состоянии квантовой запутанности). Произведём «измерение» поляризации этих двух монет (фотонов). Измерение фотонов производится с помощью поляризаторов, а «измерение» монет произведём их бросанием на стол. Каков результат этого эксперимента? Сколько бы мы ни измеряли запутанные фотоны, сколько бы, соответственно, мы ни подбрасывали монеты, мы всегда получаем один и тот же результат: если спин одного фотона направлен вверх, то спин второго направлен вниз. Соответственно, если одна монета упала решкой вверх, то вторая обязательно упала решкой вниз. И наоборот. Такой эксперимент и демонстрирует явление квантовой запутанности. Конечно, монеты никогда не ведут себя так хитро: если одна упала решкой вверх, то другая - обязательно решкой вниз. А вот запутанные фотоны - ведут. Такое поведение запутанных частиц в 1935 году поставили под сомнение Эйнштейн, Подольский и Розен. Изложенные ими взгляды получили название «ЭПР-парадокса» [21]. В 1965 году другой исследователь – Белл математически показал ошибочность взглядов Эйнштейна [4, 19], а в 1981 году известный физик Ален Аспект подтвердил доводы Белла экспериментально [1, 2, 3, 5, 6]. Оказалось, что, действительно, запутанные фотоны вели себя в точности так, как мы выше это обрисовали: многочисленные пары фотонов поляризовались таким удивительным образом, будто чувствовали друг друга. Вот в этом и состоит удивительное свойство квантовой запутанности. Когда одна из квантовых частиц (первый фотон) получает в результате измерения некоторую поляризацию, зависящую от измерительного прибора - поляризатора, так в тот же момент другая квантовая частица получает противоположную поляризацию, что подтверждает второй измерительный прибор. Обе эти поляризации «рождаются» одновременно. Как только первая частица поляризовалась, так сразу же, мгновенно, независимо от расстояния поляризуется и вторая частица. На монетах это выглядело бы так: на северном полюсе монета упала решкой вверх, на южном в тот же самый момент другая монета упала решкой вниз. И так при каждом подбрасывании, сколько бы их ни было. О явлении запутанности стали говорить, что оно нелокально, то есть поведение частиц синхронно, но не связано с их локальной связью, не является локальным. Эйнштейн так описывал локальность связей: «... (состояние) системы S2 не зависит от того, что проделывают с пространственно отделённой от неё системой S1» [20]. «… так как во время измерения эти две системы уже не взаимодействуют, то в результате каких бы то ни было операций над первой системой, во второй системе уже не может получиться никаких реальных изменений» [21]. Следовательно, запутанные частицы не подчиняются закону локальности. Сказав это, мы, собственно, ещё не видим явного парадокса, хотя уже догадываемся, что поведение частиц как-то плохо увязывается с положениями теории относительности об ограниченности скорости передачи взаимодействия. Вроде бы частицы взаимосвязаны, вроде бы состояние от одной к другой передаётся мгновенно, но нелокальность отвергает это: нет связи и поэтому ничего не передаётся. Надо признать, что одной лишь констатации «нелокальность» недостаточно. Хочется всё-таки прояснить, что конкретно за нею скрывается. Ведь мы явно видим: поведение второй частицы предопределено поведением первой. В популярной литературе есть попытки как-то аллегорически объяснить такую «несвязанную связь». Обычно приводится пример с парой перчаток. Пара перчаток, понятное дело, это одна правая и одна левая, то есть выглядит как своеобразная «запутанность». Предположим, что одну из перчаток «втёмную» отправили в Лондон, а вторая осталась в Париже. Когда в Лондоне вскрывают посылку и видят правую перчатку, то тут же, мгновенно становится известно, что в Париже осталась левая! Чем не явление нелокальности?! И правая - левая проявилось, и к тому же мгновенно. Очевидно, что «правая - левая» сформировалось в момент разделения пары перчаток. А что, если и квантовые частицы в момент запутывания тоже сформировались и затем просто сообщили измерительным приборам свои состояния? Возможно, ЭПР-парадокс появился исходя из подобных же соображений. Действительно, при его создании Эйнштейн ввёл понятие «элементов физической реальности», которые несли в себе информацию о поляризации и проявляли её при измерении частиц. Впоследствии вместо этих элементов стали говорить о «дополнительных переменных» или «скрытых параметрах». А теории, использующие эти взгляды назвали «теориями с дополнительными переменными (параметрами)». Но, как мы упомянули выше, Белл математически показал, что такие теории не в состоянии объяснить всю полноту поведения запутанных частиц. Они вели себя более зависимо, «коррелированно», чем это допускали скрытые параметры. Более того, из квантового формализма известно, что частицы не только не имели предопределённых поляризаций, они вообще их не имели. Это свойство частиц называется «суперпозицией состояний». Продемонстрируем это свойство на примере «запутанных» шаров. Допустим, у нас есть ящик, в котором лежат два шара - чёрный и белый. Если мы вынимаем один из них, то видим, что он белый. Следовательно, в ящике остался чёрный. Не глядя разложим шары по ящикам и расставим их в разные стороны. Мы можем сказать: в одном из ящиков чёрный шар, в другом - белый. Это неправильно. Каждый из шаров одновременно чёрный и белый. Если мы достанем один из шаров, то только в этом случае он станет либо чёрным, либо белым. И тут же, мгновенно второй из шаров станет белым или чёрным (противоположно первому). Это и есть правильное описание квантовой запутанности. Если один шар стал чёрным, то другой стал белым. Пока один шар не стал чёрным, то и другой не стал белым. Как только один – черный, так другой сразу же – белый. Про перчатки такого сказать нельзя. Ситуацию можно описать формулой «ЕСЛИ одни шар стал чёрным, ТО другой шар стал белым». То, что один из шаров стал чёрным – это независимое событие. Шар равновероятно мог стать либо чёрным, либо белым. То есть вероятность того, что шар станет чёрным, равна 1/2. А вот вероятность того, что второй станет противоположно белым зависит строго от состояния (цвета) первого шара. То есть, это однозначно определённое событие. При этом для того, кто вынимает этот второй шар, он будет либо белым, либо чёрным с той же вероятностью 1/2. В квантовой механике такая корреляция называется полной. Однако в реальности можно обеспечить и более мягкие условия, в которых второй шар может получить такой же цвет, что и первый. В экспериментах Алена Аспекта с запутанными фотонами использовалась такая неполная корреляция. Скажем, если первый шар стал чёрным, то второй станет белым не с достоверностью, а с некоторой конечной, отличной от единицы вероятностью. Установим вероятность того, что второй шар станет белым, когда первый шар стал чёрным, равной cos2(φ), где φ – некоторый произвольный заранее заданный параметр. Из этого условия следует, например, что если φ = π/4, то cos2(φ) = 1/2. Это значит, что если первый шар получил цвет чёрный, то второй шар равновероятно может получить цвет как белый, так и чёрный. Соответственно, если первый шар получил цвет белый, то второй шар равновероятно получит цвет либо чёрный, либо белый. Фактически это означает, что оба события – получение каждым из шаров определённого цвета – являются как бы независимыми. Ведь первый шар получает цвет равновероятно чёрный или белый. Независимо от этого второй шар тоже как бы равновероятно получает цвет либо белый, либо чёрный. Мы не можем даже с минимальной определённостью предсказать цвет каждого из шаров. Известно только, что при выемке первого шара второй сразу же приобрел какой-то цвет. Так вот, сделанное нами допущение в точности совпадает с формализмом квантовой механики. Выбранное соотношение в ней имеет название «закона Малуса»: 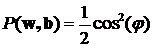 (1) (1) Уравнение показывает, что вероятность Р(w,b) получения вторым шаром белого (w) или чёрного (b) цвета равна произведению двух независимых событий: с вероятностью 1/2 (получение первым шаром чёрного цвета) и с вероятностью cos2(φ) того, что второй шар получит противоположный цвет. Рассмотрим крайние значения этого уравнения φ =0 и φ =π/2. 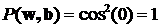 (2) (2) Из уравнения следует, что вероятность получения вторым шаром противоположного цвета равна 1. То есть во всех измерениях (испытаниях) всегда второй шар будет иметь противоположный цвет. Если же мы зададим значение параметра φ =π/2, то вероятность будет: 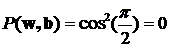 (3) (3) Это означает, что вероятность получения вторым шаром противоположного цвета равна нулю. То есть во всех измерениях (испытаниях) второй шар всегда будет иметь цвет, совпадающий с цветом первого шара. При этом в обоих случаях вероятность получения первым шаром одного из цветов всегда равна 1/2, то есть равновероятно шар будет либо белым, либо чёрным. Это уравнение мы задали произвольно, априори, не накладывая на процесс никаких других условий. Посмотрим, что следует из этого уравнения. Мы умышленно представили его как произведение двух величин: 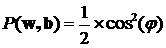 (4) (4) Если обратиться к формализму классической теории вероятностей, то можно заметить, что это уравнение фактически имеет вид теоремы умножения вероятностей, которая гласит, что «вероятность произведения двух событий (совместного появления этих событий) равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже наступило». И это описание полностью отвечает условиям нашего эксперимента с шарами. Действительно, первый сомножитель - это вероятность обнаружения первого шара с некоторым определённым цветом. Он либо белый, либо чёрный с вероятностью 1/2. На второе измерение мы наложили условие: второй шар будет иметь противоположный цвет к первому с вероятностью cos2(φ). Следовательно, это уравнение в нашем случае однозначно может трактоваться как теорема умножения вероятностей классической теории вероятностей. Однако уточним всё-таки, действительно ли события являются условно независимыми. Сначала определим чётко эти события. Событие первое: «Первый шар приобретает чёрный цвет». Очевидно, что эта вероятность однозначно определена и равна 1/2. Понятно, что шар равновероятно получит либо чёрный, либо белый цвет. Это событие является независимым. Какой бы цвет впоследствии ни получил второй шар, вероятность получения первым шаром чёрного или белого цвета неизменна. Событие второе: «Второй шар приобретает белый цвет, когда первый шар получил чёрный цвет». Наложенное нами выше условие делает это событие зависимым от первого. Если первый шар приобрёл черный цвет, тогда и только тогда второй шар может приобрести белый цвет. Если первое событие не наступило, то вероятность получения вторым шаром белого цвета либо не определена, либо цвет будет равновероятно чёрным или белым. То есть вероятность наступления второго события зависит от события первого. По правилам классической теории вероятности: «Два события А и В называются зависимыми, если появление одного из них изменяет вероятность появления другого» [7]. Получается, что два события по выемке шаров являются в нашем случае зависимыми. Как было сказано выше, это уравнение совпадает и по внешнему виду, и по описанию с квантовым уравнением закона Малуса [5]: 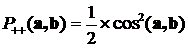 (5) (5) В этом уравнении параметры (a,b) имеют конкретное физическое значение. Это угол между осями измерительных поляризаторов. И что интересно, в противоположность рассмотренному нами эксперименту с шарами, в квантовой механике события, описываемые законом Малуса, считаются независимым. Соответственно, при вычислении вероятности наступления совместных событий используется не классическая теория вероятности, а так называемая квантовая теория вероятности: «Сложение волновых функций (амплитуд вероятностей), а не вероятностей (определяемых квадратами модулей волновых функций) принципиально отличает квантовую теорию от классической статистической теории, в которой для независимых событий справедлива теорема сложения вероятностей» [8, c.8]. Этот довод при объяснении ЭПР-парадокса можно услышать довольно часто. Отрицая зависимость событий, которая неявно требует обмена сигналами, утверждается, что вероятности вычисляются по другим, квантовым правилам. То есть события в ЭПР-парадоксе изначально объявляются независимыми и квантовому правилу сложения амплитуд вероятностей (дающим, к слову, верный результат) противопоставляется правило сложения вероятностей классической теории. Однако указанное правило классической теории совершенно непригодно для использования в нашем эксперименте с шарами. Оно звучит так: «Вероятность наступления в некоторой операции какого-либо одного (безразлично какого именно) из результатов А1, А2, ..., Аn равна сумме вероятностей этих результатов, если каждые два из них несовместимы между собой». Это неправильное применение к парадоксу ЭПР классической теории вероятностей, ведь в парадоксе ЭПР результаты наступают не «какой-либо один», а оба одновременно. Причём, более того, несовместимые события - это события вообще никогда одновременно не наступающие! Поэтому правило сложения вероятностей здесь совершенное неуместно. Но цель этого противопоставления очевидна: обосновать нелокальность. Она явочным порядком отрицает положения традиционной теории вероятности на зависимые и независимые события и обосновывает новые положения – квантовую вероятность, квантовые правила вычисления вероятности событий (сложение амплитуд вероятностей). Только так можно сохранить лоренц-инвариантность и исключить конфликт квантовой механики со специальной теорией относительности. Но, во-первых, подобный компромисс служит почвой для возникновения мистических взглядов на природу (нелокальность имеет все признаки паранормального, мистического явления), и, во-вторых, похоже, что отстоять лоренц-инвариантность не удалось [12, 18]. Главным Арбитром в этом вопросе признан знаменитый физик-экспериментатор Ален Аспект. Рассмотрим его доводы в пользу нелокальности. В процессе исследования явления нелокальности (это наша трактовка, поскольку, в сущности, эксперименты были направлены именно на это) Ален Аспект приводит аналитические обоснования на примере мысленного эксперимента Эйнштейна-Подольского-Розена (эксперимента ЭПР). В слегка изменённом виде этот эксперимент можно изобразить следующим образом:  Рис.2 Мысленный эксперимент Эйнштейна-Подольского-Розена с фотонами (подобие схемы, взятой из работы Алена Аспекта). Два фотона v1 и v2, испускаемые источником S, проанализированы линейными поляризаторами в направлениях a и b. Это оптический вариант мысленного эксперимента ЭПР в версии Бома [5]. Источник S испускает пару фотонов с различными частотами v1 и v2, разлетающихся противоположно. Предположим, что вектор состояния поляризации, описывающий пару: 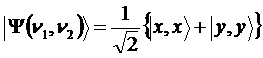 (6) (6) где |x> и |y> - линейные состояния поляризации. Это состояние замечательно: не может быть разложено на два состояния, привязанных к каждому фотону, так что мы не можем приписать никакого определенного состояния каждому фотону. В частности мы не можем назначать никакую поляризацию для каждого фотона. Такое состояние, описывающее систему нескольких объектов, о которых можно думать только глобально, является запутанным состоянием. Мы производим линейные измерения поляризации на этих двух фотонах анализаторами I и II. Анализатор I в направлении a имеет два выхода, снабженные датчиками и дает результаты + или - на соответствующем датчике, если встречена линейная поляризация параллельная или перпендикулярная к a. Анализатор II в направлении b действует аналогично. Как и для шаров рассмотрим характерные (крайние) значения угла между поляризаторами. Если угол (a,b) между измерительными осями поляризаторов равен нулю, то на их выходе фотоны всегда будут иметь одинаковую поляризацию с единичной вероятностью, то есть всегда будут регистрироваться пары соответствующими датчиками+ на обоих анализаторах: 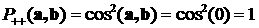 (7) (7) Это значит, что если первый фотон из пары принят датчиком+ анализатора I, то второй фотон обязательно будет принят датчиком+ анализатора II, и наоборот. Если же первый фотон из пары принят датчиком- анализатора I, то и второй фотон будет принят датчиком- анализатора II, и наоборот. Когда угол между поляризаторами равен π/2, то на их выходах фотоны никогда не будут иметь одинаковую поляризацию и всегда будут регистрироваться в противоположных каналах своих поляризаторов, и на одноименных выходах датчиков+ анализаторов никогда не будут регистрироваться фотоны одновременно: 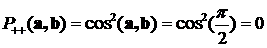 (8) (8) Такое сходство квантовых уравнений для фотонов не случайно совпадает с изобретёнными выше уравнениями для наших черно-белых «квантовых» шаров. Это два тождественных процесса. Поэтому, как и выше, здесь мы тоже имеем полное право допустить, что квантовые частицы – фотоны, подчиняющиеся закону Малуса, описываются классической теорией вероятности как два зависимых события. Однако в квантово-механическом описании этих процессов принято считать эти события независимыми. Насколько обоснованно наше заключение, противоречащее квантово-механическому, что события в эксперименте с запутанными фотонами следует считать зависимыми? Такая зависимость событий друг от друга хорошо заметна. Действительно, поляризация второго фотона зависит от поляризации первого. Ален Аспект так описывает это явление: «Когда измерение на v1 сделано, фотон v2, который не имел определенной поляризация перед этим измерением, проектируется в состояние поляризации, параллельное результату измерения на v1. Это очень удивительно, потому что это изменение в описание v2 происходит мгновенно, безотносительно расстояния между v1 и v2 в момент первого измерения» [5]. Недвусмысленно, однозначно, предельно определенно: «Когда сделано», тогда «проектируется». Налицо причинно-следственные отношения. Причина: «сделано измерение», следствие: «проектируется». «Как только сделано» первое, так сразу же наступает второе - «проектируется». Тем не менее, квантовая механика в лице её ведущих физиков упорно утверждает: события являются независимыми. Главной причиной констатации этой независимости является лоренц-инвариантность, которую, понятное дело, никто из квантовых физиков сомнению не подвергает. Напомним, что квантовый формализм даёт верные предсказания в этих экспериментах. Казалось бы, всё просто замечательно, и беспокоиться не о чем. Однако неизбежной платой за спасение лоренц-инвариантности стало введение понятия нелокальности, которая должна была окончательно снять все вопросы о зависимости событий «когда сделано - тогда проектируется». Тем не менее, вопрос остался: как же всё-таки объяснить это самое никуда не девшееся «когда сделано - тогда проектируется»?! Нелокальность в этом случае получила явные признаки мистического, паранормального явления: визуально зависимость имеется, но формально её нет. Присмотримся к этому противоречию более внимательно. Начнём с того, что попробуем конкретизировать, о каких же событиях, собственно, идёт речь? Закон Малуса, верно описывающий явление, имеет вид: 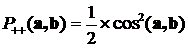 (5) (5) В этом уравнении виден ещё один довод в пользу квантово-механической трактовки процесса как независимых событий. Мы видим, что справа от знака равенства стоит произведение двух величин. Случайно или нет, но оно выглядит как произведение двух вероятностей (события А и события В). Из классической теории вероятностей известно: «Если для событий А и В выполняется равенство Р(АВ)=Р(А)Р(В), то эти события независимы». Иногда эту теорему называют обратной теоремой умножения вероятностей, иногда признаком того, что события являются независимыми. «Что такое независимые события в жизни - понятно каждому. Это значит, что между событиями отсутствует причинно-следственная связь, осуществление одного никак не влияет на другое». Казалось бы, приведённое уравнение явно подпадает под это определение. Действительно, вероятность события А «регистрация фотона датчиком+ анализатора I» - это Р(А) = 1/2; вероятность события В «регистрация фотона датчиком+ анализатора II» - это Р(В) = cos2(a,b); результирующая вероятность «совместная регистрация фотонов датчиками+ анализаторов I и II» - это Р(АВ). О чём теперь можно спорить?! Есть о чём. Дадим словесное описание этого уравнения в виде, удобном для нашего анализа. Вероятность Р(АВ) - это «вероятность того, что фотоны будут зарегистрированы одновременно в + каналах поляризаторов, которая зависит от угла между поляризаторами». Обратим внимание, что в этом описании угол между поляризаторами подразумевает как расстояние между ними, так и время между измерениями. Действительно, когда фотоны разлетелись, ничто не мешает нам повернуть эти поляризаторы (что, кстати, проделывал и Ален Аспект). И любой поворот в любое время будет учтён в момент прохождения поляризаторов фотонами (эксперименты Аспекта это подтвердили)! Угол определяется обоими поляризаторами независимо от расстояния и времени полёта вопреки утверждению Эйнштейна: «... (состояние) системы S2 не зависит от того, что проделывают с пространственно отделённой от неё системой S1». В момент второго измерения об изменении положения первого поляризатора сразу же становится известно второму поляризатору. Другими словами, этот угол (положение удалённого поляризатора) может постоянно изменяться, но в момент прихода фотонов он становится однозначно определённым. В момент прохождения второго фотона через свой поляризатор, этот второй фотон примет свою поляризацию, которая однозначно определяется положением первого поляризатора (углом с ним)! Этот второй фотон получит не какую-то, неизвестно откуда взявшуюся поляризацию, а поляризацию, которая зависит от положения удалённого от фотона первого поляризатора. Как можно произвести решение уравнения Малуса традиционным способом? Мы определяем (фиксируем, вычисляем, измеряем) угол близлежащего к нам (второго) поляризатора. Затем получаем (по почте, по телефону, по радио или глядя в телескоп) угол (положение) удалённого (первого) поляризатора и вычисляем как разницу результирующий угол. После чего подставляем его значение в уравнение закона. Результат наших вычислений зависит от получения положения удалённого поляризатора. В описанных обстоятельствах отрицать зависимость событий в экспериментах Аспекта (в парадоксе ЭПР, в законе Малуса) - полный абсурд. С учетом сказанного, попробуем дать другое определение событиям, которые описываются квантовой нелокальностью в этом эксперименте и которые входят (похоже, незаметно для многих) в уравнение закона Малуса. Очевидно, первым событием А остаётся событие «Регистрация первого фотона в + канале регистратора». Это автономное, независимое событие, имеющее вероятность наступления 1/2. Нет никаких указаний на то, что это значение вероятности может быть изменено каким-либо способом. Ничто не может повлиять на исход первого измерения. При любом измерении эта величина вероятности остаётся неизменной, то есть на неё в принципе не оказывается никакого влияния. Либо это такое «влияние», которое никак не изменяет результат. Но этого нельзя сказать о втором измерении. Его результат явно зависит от результата первого измерения. Второе событие (событие В) никогда не наступит, пока не наступит первое! А в чем состоит оно, это второе событие? Правильным следует считать такое определение второго события: «Регистрация второго фотона в + канале регистратора, который повёрнут под углом к первому регистратору при условии, что первый фотон был зарегистрирован в + канале регистратора», то есть, когда событие А наступило. В такой формулировке событие В является условно зависимым от события А. Вероятность этого события равна: PА(В) = cos2(θ) (9) где: θ –угол между поляризацией фотона и поляризатора, который с учетом условий нашего эксперимента в точности равен углу между поляризаторами. Невозможно представить себе совместное обнаружение фотонов, если один из регистраторов не обнаружил фотона. Это означает, что наступление второго события возможно тогда и только тогда, когда наступило событие первое. Классическая теория вероятностей это объявляет признаком зависимости событий: «Два события А и В называются зависимыми, если появление одного из них изменяет вероятность появления другого». Если второе событие не наступило, то вероятность совместного обнаружения фотонов - событие недостоверное: «Два события считаются независимыми, если вероятность одного из них не зависит от появления или не появления другого события». Если второе событие наступило - то вероятность совместного обнаружения фотонов становится определённой величиной. То есть, мы твёрдо убеждены, что описанные два события, входящие в выражение закона Малуса - зависимые. Но как же быть с определением независимости событий, приведённым выше? Возникает двусмысленность? Нет. В той же классической теории вероятностей есть такое определение: «Теорема умножения вероятностей. Вероятность произведения двух событий (совместного появления этих событий) равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже наступило: Р(АВ) = Р(А)РА(В)». Кроме того есть определение, проводящее связь между приведёнными формулировками теорем умножения: «Определение. Событие В называется независимым от события А, если появление события А не изменяет вероятности В, то есть РА(В) = Р (В)». Что следует из приведённых доводов? Главное: события при измерении двух удалённых фотонов являются зависимыми. А это означает, что между ними имеется какая-то связь, которая противоречит лоренц-инвариантности. То есть, квантово-механическая запутанность противоречит теории относительности Эйнштейна. С позиции релятивистской теории не могут два удалённых объекта взаимодействовать, передавать друг другу какую-либо информацию быстрее скорости света. Налицо противоречие между явлением нелокальности квантовой механики и специальной теорией относительности. Противоречие это возникло при попытке отказаться от мистической квантово-механической нелокальности и использовании для объяснения явления запутанности положений классической теории вероятности. От нелокальность мы отказались, но взамен получили противоречие с лоренц-инвариантностью. Нелокальность - это мистическое синхронное поведение объектов при отсутствии между ними какой бы то ни было связи. Трактовка с позиции классической теории вероятности - это признание сверхсветовой связи между объектами. Этакое абсурдное воплощение эйнштейновского локального реализма, «призрачного дальнодействия», как его называл Эйнштейн [13, 16]. Однако, мы не склонны считать это подменой одного мистического явления другим. Сверхсветовой синхронизм поведения - физический факт. Более того. Следует ожидать, что этот факт должен проявиться и в чём-либо ещё. И такое проявление имеет под собой весьма веские основания, позволяя поставить под вопрос истинность специальной теории относительности. Противоречие между КМ и СТО Какого-либо сигнала, с помощью которого квантовые частицы обмениваются информацией, до настоящего времени не зафиксировано. В своих экспериментах Аспект регистрировал сверхсветовое взаимное влияние состояния одной частицы на состояние другой, но передачи информации при этом обнаружено не было. Тем не менее, явление запутанности позволяет в принципе организовать проведение эксперимента, который явным образом может трактоваться как демонстрация информационной сверхсветовой связи между частицами, что в свою очередь позволяет показать синхронность хода часов, движущихся друг относительно друга. Это означает, что утверждение СТО о том, что движущиеся часы отстают, - противоречит явлению нелокальности. Отсюда следует вывод, что между квантовой теорией и специальной теорией относительности существует неустранимое противоречие, касающееся скорости передачи взаимодействия и квантовой нелокальности. Рассмотрим мысленный эксперимент [15, 11, 9, 10, 17], который показывает, что часы в движущихся друг относительно друга ИСО идут синхронно вопреки положениям СТО. Соберём экспериментальную установку из трёх ИСО: лабораторной (неподвижной) и двух ИСО А и В, движущихся навстречу друг другу с одинаковыми скоростями относительно неподвижной ИСО. 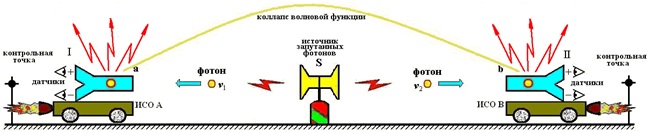 Рис.3 Две движущиеся инерциальные системы с точки зрения неподвижной ИСО. Источник запутанных фотонов неподвижен и фотоны из каждой пары приходят в движущиеся ИСО одновременно. Строенные стрелки-молнии указывают на точки, в которых находились фотоны в момент коллапса волновой функции. Движение двух ИСО А и В с точки зрения неподвижной ИСО происходит в сторону источника запутанных фотонов S с одинаковой удаленности от него таким образом, что фотоны v1 и v2 из каждой пары достигают каждый своей ИСО одновременно. Мы производим линейные измерения поляризации этих двух фотонов анализаторами I и II. Анализатор I в направлении a (справа налево) снабжен двумя датчиками и дает результаты + или -, если встречена линейная поляризации параллельная или перпендикулярная к a. Анализатор II в направлении b (слева направо) действует аналогично. Не трудно заметить, что установка в общих чертах соответствует мысленному эксперименту Эйнштейна-Подольского-Розена-Бома с фотонами, приведенному в статье Алена Аспекта [3, 5, 6, 2, 1]. Установим скорость сближения двух ИСО равной приблизительно 0,86с, что соответствует релятивистскому замедлению времени в 2 раза. Расстояние между ИСО А и В выберем таким, что каждая из ИСО достигнет источника фотонов S через 2 часа. Фотоны v1 и v2 достигают измерителей I или II, в результате чего происходит коллапс волновой функции, описывающей их состояние. Жёлтой линией условно показана нелокальная связь частиц, условный путь передачи так называемой «квантовой информации». При этом частицы приобретают собственные состояния (на рисунке это условно показано «молниями»). В процессе движения этих ИСО показания измерительных приборов регистрируются на каком-либо носителе. Когда две ИСО сойдутся в точке размещения источника запутанных фотонов S, анализ полученных данных покажет [15], что часы в двух движущихся относительно друг друга ИСО идут синхронно. При этом СТО вынуждена дать предсказания о наступлении одного и того же события в двух разных местах. Эти два взаимоисключающих предсказания являются следствием предположения, что коллапс волновой функции происходит мгновенно независимо от расстояния между объектами. Мгновенная передача сигнала в СТО невозможна и собственно передачи сигнала в этом мысленном эксперименте не зарегистрировано, достигнуто лишь мгновенно-одновременное снятие показаний движущихся часов. Литература: 1. Aspect A., Dalibard J., Roger G., Experimental Test of Bell’s Inequalities Using Time-Varying Analysers. – Phys. Rev. Lett. 49, 25, (1982). (http://kh.bu.edu/qcl/pdf/aspect_a1982707d6d64.pdf) 2. Aspect A., Grangier P., Roger G., Experimental Realization of Einstein-Podolsky-Rosen-Bohm Gedankenexperiment: A New Violation of Bell’s Inequalities. – Phys. Rev. Lett. 49, 2, (1982). 3. Aspect А. «Bell’s theorem: the naive view of an experimentalist», 2001, (http://quantum3000.narod.ru/papers/edu/aspect_bell.zip) 4. Bell J.S., On the Einstein Podolsky Rosen paradox, Physics Vol.1, No.3, pp.198-200, 1964 5. Ален Аспект, Теорема Белла: наивный взгляд экспериментатора, (Пер. с англ. Путенихина П.В.), Квантовая Магия, 4, 2135 (2007). http://quantmagic.narod.ru/volumes/VOL422007/p2135.html 6. Ален Аспект, Теорема Белла: наивный взгляд экспериментатора, (Пер. М.Х.Шульмана), Институт исследований природы времени, 2006, http://www.chronos.msu.ru/RREPORTS/aspek_teorema_bella.pdf 7. Лекция 3. Теоремы сложения и умножения вероятностей, http://apollyon1986.narod.ru/docs/TViMS/NP/lekziitv/LEKZIYA3.HTM 8. Огурцов А.Н. Физика для студентов. Квантовая физика. Лекции по физике, 7, http://www.ilt.kharkov.ua/bvi/ogurtsov/lect7quant.pdf 9. Путенихин П.В., Великая тайна специальной теории относительности, Квант. Маг. 7, 3101 (2010), http://quantmagic.narod.ru/volumes/VOL732010/p3101.html http://zhurnal.lib.ru/editors/p/putenihin_p_w/tajna.shtml http://www.sciteclibrary.ru/rus/catalog/pages/10341.html 10. Путенихин П.В., Главная загадка физики квантов, Самиздат, 2009, http://zhurnal.lib.ru/p/putenihin_p_w/gzfk.shtml http://sciteclibrary.ru/rus/catalog/pages/9818.html http://quantmagic.narod.ru/volumes/VOL642009/p4126.html 11. Путенихин П.В., Квантовая механика против СТО, Квантовая Магия, 4, 2130 (2007), http://quantmagic.narod.ru/volumes/VOL422007/p2130.html http://www.sciteclibrary.ru/rus/catalog/pages/8918.html http://zhurnal.lib.ru/editors/p/putenihin_p_w/kmvsto.shtml 12. Путенихин П.В., Комментарии к выводам Белла в статье «Парадокс Эйнштейна, Подольского, Розена», SciTecLibrary, 2008, http://www.sciteclibrary.ru/rus/catalog/pages/8979.html http://www.sciteclibrary.ru/texsts/rus/stat/st2213.pdf 13. Путенихин П.В., Локальный реализм Эйнштейна. – Самиздат, 2008, http://zhurnal.lib.ru/p/putenihin_p_w/localism.shtml 14. Путенихин П.В., Призрак амплитуды или Парадокс Камнева и неравенства Звонарёва (шутка с оттенком саркастического пародизма), Квантовая Магия, 5, 1112 (2008), http://quantmagic.narod.ru/volumes/VOL512008/p1112.html http://www.sciteclibrary.ru/rus/catalog/pages/9032.html http://zhurnal.lib.ru/editors/p/putenihin_p_w/amplitude.shtml 15. Путенихин П.В., Противоречие между квантовой механикой и СТО, Квант. Маг. 7, 3115 (2010), http://quantmagic.narod.ru/volumes/VOL732010/p3115.html http://www.sciteclibrary.ru/rus/catalog/pages/10373.html http://zhurnal.lib.ru/editors/p/putenihin_p_w/protiv.shtml 16. Путенихин П.В., Сущность локализма, Квантовая Магия, 5, 2201 (2008), http://quantmagic.narod.ru/volumes/VOL522008/p2201.html http://www.sciteclibrary.ru/rus/catalog/pages/9072.html 17. Путенихин П.В., Три ошибки анти-СТО, SciTecLibrary, 2011, http://www.sciteclibrary.ru/rus/catalog/pages/11390.html http://zhurnal.lib.ru/p/putenihin_p_w/antisto.shtml 18. Путенихин П.В., Эксперимент по схеме Аспекта с источником псевдо-запутанных частиц, Квантовая Магия, 4, 2167 (2007), http://quantmagic.narod.ru/volumes/VOL422007/p2167.html http://www.sciteclibrary.ru/rus/catalog/pages/9016.html http://zhurnal.lib.ru/p/putenihin_p_w/pseudo.shtml 19. Путенихин П.В.: Bell J.S., On the Einstein Podolsky Rosen paradox (перевод с англ. - П.В.Путенихин; комментарии к выводам и оригинальный текст статьи), Квантовая Магия, 5, 2160 (2008), http://quantmagic.narod.ru/volumes/VOL522008/p2160.html http://zhurnal.lib.ru/editors/p/putenihin_p_w/bell.shtml 20. Эйнштейн А. Собрание научных трудов в четырех томах. Том 4. Статьи, рецензии, письма. Эволюция физики. М.: Наука, 1967, http://eqworld.ipmnet.ru/ru/library/books/Einstein_t4_1967ru.djvu 21. Эйнштейн А., Подольский Б., Розен Н. Можно ли считать квантовомеханическое описание физической реальности полным? / Эйнштейн А. Собр. научных трудов, т. 3. M., Наука, 1966, с.604-611 http://eqworld.ipmnet.ru/ru/library/books/Einstein_t3_1966ru.djvu | |
| Категория: Разное | | |
| Просмотров: 1755 | Загрузок: 0 | |
| Всего комментариев: 0 | |