Путенихин П.В. Пространственное линзирование
| [ Скачать с сервера (761.3 Kb) ] | 12.02.2016, 21:30 |
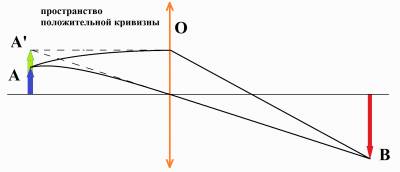
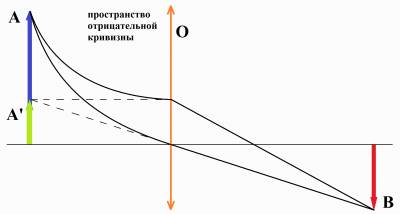
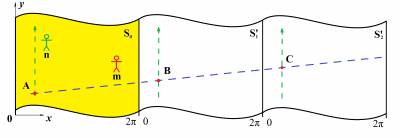
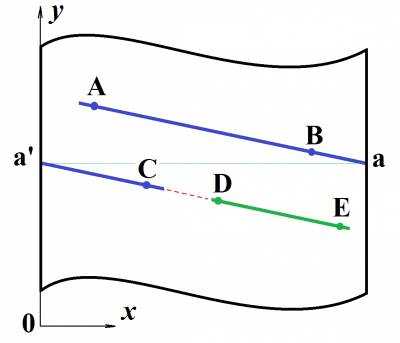
Полный текст статьи находится во вложении. Далее представлен фрагмент текста для ознакомления. Путенихин П.В. m55@mail.ru Аннотация Кривые пустые пространства обладают свойствами линзы. Плоское пространство Евклида можно замкнуть процедурой отождествления с сохранением локальной евклидовой метрики, не наделяя его свойствами линзы. Отождествление дополнительных измерений в теории струн может устранить из неё многообразия Калаби-Яу и сократить ландшафт теории. Ключевые слова Изотропия, линзирование, затылок, изометричные поверхности, третий постулат Евклида, отождествление, склейка, трёхсторонний квадрат, триквадрат, трёхгранный куб, трикуб, двухосевой цилиндр, сферический цилиндр, трехмерный тор, двухсторонний квадрат, биквадрат В космологии известно такое явление как гравитационное линзирование. Заключается оно в том, что пространство, искривлённое вблизи массивных тел, например, чёрных дыр, проявляет себя как линза. Свет, проходя через такую линзу, искривляется, фокусируется как от обычной стеклянной линзы. Подобными же свойствами обладает и пустое пространство, без массивных тел, если это замкнутое искривленное пространство. Описание свойств таких пространств в литературе можно встретить довольно часто: сферическое пространство Римана, пространство постоянной отрицательной кривизны Лобачевского. Если пространство имеет положительную кривизну, то луч света, выпущенный в каком-либо направлении, через некоторое время вернётся к источнику с обратной стороны. Есть весьма красочное описание этого явления: в таком пространстве, как говорится, можно увидеть собственный затылок: «виден с разных сторон и в разные моменты времени за счет того, что свет много раз успевает обойти такой замкнутый мир за время расширения» [3]. Как модель пространства космологической замкнутой Вселенной часто рассматривают надувной шарик (сферическое пространство). При его раздувании макеты галактик, наклеенные на его поверхности, отдаляются друг от друга, оставаясь всегда в одной и той же точке координатной сетки. Очевидно, что луч света, выпущенный в таком пространстве, опояшет его и вернётся в исходную точку. Луч света в пространстве - это прямая линия. Светоносной средой для сферы является её поверхность. Поэтому луч света, двигаясь по этому пространству, повторяет его контуры – сферу. Для этого условного луча света нет направлений внутрь и от сферы, он распространяется по ней вдоль линий больших кругов. Параллельные линии на сфере - это две большие окружности, проведённые через две рядом расположенные точки. Очевидно, что две такие параллельные линии пересекутся дважды. Отсюда следует, что все прямые линии, проведённые из одной точки, во-первых, пересекутся ещё раз, во-вторых, являются параллельными. Это один из примеров нарушения пятого постулата Евклида, в соответствии с которым, через точку можно провести только одну прямую, параллельную данной, то есть, не пересекающую её. В сферическом пространстве (положительной кривизны) таких прямых не существует. Из приведённого описания можно заметить достаточно очевидную особенность такого пространства. Вопреки распространенному мнению, увидеть в таком пространстве свой затылок невозможно в принципе. Все лучи света, испущенные из точки, вернутся именно в эту точку. Это значит, что в какую бы область неба мы ни посмотрели, мы обязательно будем видеть лучи света, «испущенные нашим затылком». Изображение его будет «размазано» по всей сфере небосвода или видимой его части. Понятно, что для этого в пространстве Вселенной не должно быть ни других мешающих источников света, ни его поглотителей. Тем не менее, подобные «изображения затылка» всё-таки имеют характерное, довольно интересное свойство. Возьмём, например, фотопластинку и на её тыльной стороне поместим источники света в виде ярких точек. Подождём достаточно долго и посмотрим на лицевую сторону фотопластинки. На ней проявится точное изображение этих точек, каждое напротив своего источника, находящегося на тыльной стороне. То есть, мы сделали своеобразную фотокамеру, которая будто бы сфотографировала источники. Но у этой камеры нет ни линзы, ни тонкого обскурного отверстия. Изображение мы получили благодаря эффекту пространственного линзирования. В качестве линзы выступило само положительно искривлённое пространство. Этот эффект можно наблюдать только тогда, когда источник и фотопластинка находятся в одной точке пространства. Если источник и приёмник находятся в разных точках пространства, то картина будет иной. Рассмотрим объект - стрелку А, находящуюся от экрана на расстоянии, много меньшем, чем длина окружности сферического мира. Очевидно, что лучи от точек источника не сойдутся в соответствующих точках на экране, поскольку они не диаметрально противоположные. Все лучи от точек объекта А будут распространяться в сторону экрана не по евклидовым параллельным линиям, а по дугам больших окружностей сферы. Поставим перед экраном обычную оптическую линзу О. Если пространство обычное, евклидово, то объект А отобразится на экране в изображение В. Если же это пространство имеет сферическую кривизну, то такое же изображение В будет эквивалентно изображению от объекта А': Физически объект А меньше объекта А', дающего такое же изображение В. То есть, как видно из рисунка, сферическая искривлённость пространства (пространство поверхности сферы) увеличивает изображение удалённого объекта. Точно также, если трехмерное пространство Вселенной замкнутое, сферическое, то все объекты во Вселенной, удалённые от нас, мы будем видеть увеличенными. Чем сильнее искривлено пространство, тем сильнее будет увеличение. Такая картина будет в пространстве положительной кривизны. Но тогда возникает естественный вопрос, а каким будет изображение в пространстве отрицательной кривизны? Легко догадаться: если в плоском пространстве мы получаем неискаженное изображение, а в пространстве с положительной кривизной - увеличенное, то в пространстве отрицательной кривизны мы должны получить изображение уменьшенное. В пространстве отрицательной кривизны лучи света от источника расходятся, как показано на рисунке: Каждый из прожекторов испускает поток параллельных лучей света. Но в пространстве положительной кривизны (сферический мир Римана) эти «параллельные» лучи на удалении сходятся, а в пространстве отрицательной кривизны (мир Лобачевского) эти «параллельные» лучи света расходятся. С учетом такого поведения «параллельных» линий в пространстве отрицательной кривизны, рассмотренный нами выше объект по сравнению с плоским пространством отобразится на экране уменьшенным: На рисунке объект А' - это источник в плоском пространстве, видимый через оптическую линзу О как изображение В. Такое же изображение B в искривленном пространстве отрицательной кривизны будет получено от объекта А, который больше объекта А'. Следовательно, пространство отрицательной кривизны обладает свойствами рассеивающей линзы. Замкнутые пространства Евклида Очевидно, что эффекты пространственного линзирования и возможность увидеть свой затылок присущи только замкнутым пространствам. В случае двухмерного пространства этим свойством обладают, например, такие хорошо известные поверхности: сфера, псевдосфера Бельтрами, тор, цилиндр, конус. Все эти поверхности не являются плоскостями Евклида. Очевидно, что изначально геометрия Евклида создавалась как геометрия плоского изотропного мира, хотя явно это не указано. Ни о какой замкнутости евклидова пространства не было и речи. Впоследствии основные её положения (с существенными изменениями) довольно успешно были перенесены на замкнутые искривлённые сферическое и гиперболическое пространства. Однако, известно, что и сама геометрия Евклида имеет свой собственный евклидов замкнутый мир. Свернём, к примеру, в цилиндр лист с нарисованными параллельными прямыми. На поверхности цилиндра определение параллельности останется верным. Прямые теперь стали геодезическими, но они в точности повторяют все свойства плоских прямых линий Евклида. «Замыкание» в кривое евклидово пространство без пересечения может быть осуществлено сворачиванием плоскости Евклида только в цилиндр или в конус. Эти поверхности являются изометричными по отношению к обычной плоскости Евклида: «Изометричные поверхности — поверхности в евклидовом или римановом пространстве такие, что между ними можно установить взаимно однозначное точечное соответствие, при котором каждая спрямляемая кривая одной из поверхностей имеет своим образом тоже спрямляемую кривую и той же длины» [2]. На то, что геометрия на поверхностях конуса или цилиндра сохраняет свойства геометрии на плоскости Евклида, обращали внимание, например, Риман: «цилиндрические или конические поверхности существенно не отличны от плоскости, так как могут быть получены из плоскости посредством одного лишь изгибания, причем внутренние метрические отношения остаются неизменными и все теоремы, касающиеся этих отношений, то есть вся планиметрия, остаются в силе» [6]. На это указывал и Рашевский: «Термин «изгибание» связан с наглядным представлением о поверхности как о гибкой, но нерастяжимой и несжимаемой пленке; такую пленку можно изгибать в пространстве, меняя ее форму, но сохраняя длины всех кривых на ней. Примером может служить свертывание плоского листа бумаги в цилиндр или конус» [4]. Однако, следует уточнить, что эти пространства являются пространствами Евклида лишь локально, ограниченно. На конусе (если угол сегмента развертки меньше π) и цилиндре нарушается третий постулат Евклида [1, 7]: «3. И что из всякого центра и всяким раствором <может быть> описан круг». Нарушение третьего постулата автоматически ведёт к другим ограничениям. Например, на цилиндре существуют замкнутые «прямые», что является нарушением постулата о неограниченном продлении прямой: если идти по этой прямой линии, то придёшь в исходную точку. Две пересекающиеся прямые на цилиндрической поверхности при неограниченном продлении имеют неограниченное число точек пересечения. Это означает, что внутренние наблюдатели могут экспериментально определить замкнутость своего мира. Например, два путешественника будут периодически встречаться, если один идёт перпендикулярно к замкнутой координате (то есть, вдоль оси цилиндра), а второй - не параллельно к ней в одну сторону с первым (то есть, по винтовой линии). Если они оставляют след, то эти следы будут периодически пересекаться. В кривом цилиндрическом мире Евклида можно увидеть свой затылок. На рисунке показаны несколько разверток одного и того же цилиндра, приложенных друг к другу для наглядности: Рис.4. Развертка цилиндрической поверхности S0. Для наглядности по горизонтали показаны приложенные встык друг к другу несколько разверток - S1, S2. Ось y - направление оси цилиндра. На поверхности цилиндра две параллельные прямые могут иметь множество совпадающих точек, сливаться, что нарушает аксиому Гильберта I2 группы принадлежности «Каковы бы ни были две точки А и В, существует не более одной прямой, проходящей через эти точки»: Рис.5. Развертка цилиндрической поверхности. Параллельные прямые пересекаются. Ось y - направление оси цилиндра. Показана развертка цилиндра (ось цилиндра - вертикальна). Параллельно прямой AB проведена прямая DЕ. Прямая AB продолжена до точки C и проходит под углом к оси цилиндра (не замкнута). Видно, что при дальнейшем её продолжении она сольётся с прямой DЕ. Таким же локально евклидовым пространством является и конус: на конической поверхности существуют, по меньшей мере, две прямые линии, которые при неограниченном продлении пересекаются в двух точках; могут существовать прямые линии, которые самопересекаются и, следовательно, параллельные пересекающиеся прямые. Конус образуется из плоскости Евклида склейкой двух сторон угла и сворачиванием куска плоскости. (Продолжение во вложенном файле) 05.01.13 Адрес полного текста статьи в интернете URL: http://samlib.ru/p/putenihin_p_w/linza.shtml Иллюстрации и уравнения к статье (зеркала) http://samlib.ru/editors/p/putenihin_p_w/ https://cloud.mail.ru/public/8WpP/qeaUMAiGz | |
| Категория: Разное | | | |
| Просмотров: 3481 | Загрузок: 77 | |
| Всего комментариев: 0 | |