Путенихин П.В. Логические основания многомерных пространств
| [ Скачать с сервера (662.5 Kb) ] | 10.02.2016, 12:43 |
Путенихин П.В. m55@mail.ru Аннотация Представления о Реальности, как многомерном пространственном образовании, имеют некоторые логические сложности. Если бы Реальность имела четыре или более пространственных координат, то в ней должны были бы наблюдаться явления, противоречащие известным физическим законам, логике и обыденному здравому смыслу. Введение В настоящее время общепризнанным является представление о реальности, размещенной в четырехмерном пространстве – времени. Это пространство - время представляет собой совокупность трёх пространственных координат и одной временной, которая включена в эту совокупность со своими специфическими особенностями. Во-первых, временная координата входит со знаком, противоположным знаку пространственных координат, и, во-вторых, в виде произведения времени на скорость света, поскольку только в этом случае она получает размерность длины (пространственную). Полученное образование носит название пространства-времени Минковского и имеет метрику (1, -1, -1, -1) или кратко (+ - - -). Иногда метрику записывают инверсно: (- + + +). Для системы координат главным условием, видимо, следует считать ортогональность этих координат. Простым и наглядным образом ортогональности является независимость каждой из координат от любой из остальных. В привычном представлении это выражается в перпендикулярности координатных осей. Если же рассмотреть условия формирования пространства-времени Минковского, то становится видна некоторая его условность, искусственность, ведь временная координата (произведение времени на скорость света) изначально определялась как корень из суммы квадратов трёх пространственных координат, входящих в уравнение релятивистского интервала, то есть как зависимая от этих величин. Тем не менее, в теории относительности все четыре координаты рассматриваются как ортогональные, а выводы теории при этом полностью соответствуют всем экспериментальным и наблюдаемым данным. И всё же пространственные координаты и временная координата являются не вполне тождественными, равнозначными. В частности, для любого объекта мы можем принудительно задать, зафиксировать некоторые координаты в пространстве, но не можем задать координату временную. Следовательно, такое пространство-время можно назвать неоднородным четырехмерным пространством. При этом возникает правомерным вопрос, что же тогда должно представлять собой однородное четырехмерное пространство? Имеет ли оно логическое основание? Попробуем разобраться в этом, для чего рассмотрим последовательно возможные виды однородных многомерных пространств, начиная с базового пространства с нулевой мерностью. Мерность пространства, то есть количество координат, которые это пространство описывают, мы будем обозначать латинской буквой n. Пространство нулевой мерности На первый взгляд пространство нулевой мерности не имеет смысла. Это же пространство, которого, в сущности, нет. Однако даже такому пустому пространству могут быть приписаны некоторые характеристики, свойственные любому другому пространству. Очевидно, что эти характеристики так же являются «пустыми», как и само нульмерное пространство. Например, в таком пространстве отсутствуют оси координат. В нем отсутствуют проекции в любом виде. Единственное, что можно условно приписать этому пространству, - это наличие в нём объектов с нулевыми метриками. Эти объекты имеют нульмерные протяженности, то есть нулевые длины. Но число таких объектов, как это ни покажется странным, в рамках нуль - пространства равно бесконечности. Ведь в нулевом объёме помещается бесчисленное количество нулевых объёмов (здесь мы не будем вести разговор о порядке малости). Рассмотрим бытие как материальный мир, в котором Пространство и Время рождаются в процессе возникновения вещества из Материи [1, 2, 3]. Мы не будем углубляться в такие детали, как сингулярность и Большой Взрыв, поскольку нас интересует не процесс, не механизм возникновения пространства, а его свойства. Итак, вообразим себе условно Материю, в которой нет объектов со свойствами пространства. Наблюдать Пространство Материи как таковое мы не можем, поскольку, как отмечено в [1, 2], пространство – это свойство не материи, а вещества и некоторых других проявлений свойств собственно Материи. То, что Материя изображена на рис.1 в виде пространственного объекта – это условность, ведь это такое «пространство», наблюдать которое может только Субъект, находящийся вне этой сущности, вне Материи (Бог):  Рис.1 Нульмерное пространство (точка) в Пространстве Материи, не имеющей по определению измерений Внутри фрагмента Пространства Материи изобразим точку – нульмерное пространство и рассмотрим, какими особенностями оно обладает. Поскольку мы предполагаем рассмотреть целый класс пространств, то нам необходимо выделить что-то общее в них, признаки, объединяющие эти пространства. Это позволит увидеть и понять поведение самых существенных из этих признаков. Поэтому здесь и далее мы будем исходить из следующих правил: 1. свойства данного пространства должны быть присущи и пространству большей мерности; 2. пространство большей мерности может иметь дополнительные свойства, не присущие данному пространству; 3. соотношения между смежными пространствами должны быть схожи, включая способы перехода от данного пространства к пространству большей мерности. В первую очередь нас интересует следующее соотношение между пространствами: как «видится», как воспринимается некий объект из любого пространства. Причиной этого интереса являются известные описания восприятия четырехмерного объекта из нашего трехмерного мира. Считается, что в целом невозможно «поместить» четырехмерный объект в трехмерный мир, и он воспринимается как сечение, срез этого объекта, его проекция на трехмерное пространство. Это свойственно всем смежным пространствам. Действительно, поместить, например, в нульмерное пространство одномерный объект – линию – невозможно. При прохождении такого одномерного объекта через нульмерное пространство, условные обитатели последнего могут наблюдать только то, что в принципе доступно наблюдению в этом пространстве – нульмерные объекты. То есть линия будет проецироваться в нульмерном пространстве в точку с нулевыми размерами:  Рис.2 Пересечение одномерным пространством нульмерного приводит к появлению в последнем только нульмерной проекции. Здесь и далее для наглядности мы изображаем нулевые размеры (толщину линий, объектов) некоторыми объёмными фигурами, подразумевая, что эти объёмы и размеры на самом деле равны нулю. Для «наблюдателей» (понятно, что такие наблюдатели сильно отличаются от привычных для нас трехмерных наблюдателей) нульмерного пространства возможно наблюдение лишь краткого фрагмента объекта одномерного. При этом они, очевидно, будут наблюдать удивительное явление: возникший в их мире из ниоткуда объект затем странным, необъяснимым образом изменяется. Например, одномерная линия может быть неоднородной и иметь на своём протяжении иметь различную массу или цвет. Для наблюдателя нульмерного пространства такой появившийся из ничего объект без всякой причины изменяет свою массу или цвет. Напротив, для наблюдателя одномерного мира при этом ничего странного не происходит: просто линия перемещается через эту точку. Очевидно, что такая же картина будет наблюдаться и при перемещении через нульмерное пространство другого объекта – двухмерного. Как и в первом случае, наблюдатели нульмерного пространства будут с удивлением наблюдать, возникновение из ничего объект меняет свои характеристики:  Рис.3 Пересечение двухмерным пространством нульмерного для последнего приводит к появлению лишь нульмерной проекции. Для удобства изображения движущимся показано нульмерное пространство – иначе рисунок был бы загроможден несколькими наложенными друг на друга плоскостями двухмерного объекта. На рисунке для удобства изображения движущимся показано нульмерное пространство. Если бы это пространство (красная сфера) было изображено неподвижным, то пришлось бы изобразить в движении плоскость (двухмерное пространство), что сильно затемнило бы рисунок. Двухмерное пространство приближается к нульмерному и пересекает его (условно это показано отверстием в двухмерной плоскости). В этот момент наблюдатели нульмерного пространства наблюдают возникновение в нём из ничего нового объекта, который, очевидно, обладает всеми свойствами объекта двухмерного: например, цветом, плотностью, вязкостью и другими. Плоскость двухмерного пространства может перемещаться далее таким образом (влево), что будет всегда пересекать область нульмерного пространства, всегда находясь в нём своей частью. Наблюдателям нульмерного пространства при этом будет доступна именно та часть двухмерного пространства, которая пересекается с ним. Поэтому они будут наблюдать беспричинное, ничем не объяснимое изменение свойств новоявленного образования: изменение цвета, массы, плотности и прочего. Это будет в том случае, если двухмерное пространство (плоскость) будет, соответственно, неоднородной по своей поверхности. В дальнейшем, когда двухмерное пространство, плоскость изменит направление своего движения (сместится, например, вверх) и выйдет из соприкосновения с нульмерным пространство, в последнем произойдёт чудо исчезновения этого объекта. Точно такая же картина будет наблюдаться и при пересечении нульмерного пространства объектом трехмерного пространства:  Рис.4 Пересечение трехмерным пространством нульмерного для последнего приводит к появлению лишь нульмерной проекции. Для удобства изображения движущимся показано нульмерное пространство. Движущийся вверх – по оси z – трехмерный объект (куб) в некоторый момент времени приходит в соприкосновение с нульмерным пространством, которое как бы движется сквозь этот куб вдоль изображенного на рис.3 канала. Наблюдателям нульмерного пространства будут доступны для восприятия те области куба, которые в данный момент пересекаются с ними. Если куб неоднороден, то наблюдаемые свойства будут изменяться без всякой видимой причины: плотность, цвет, диэлектрическая проницаемость, вязкость и прочее. Когда нульмерное пространство достигнет края куба и выйдет из него, в нульмерном пространстве неожиданно исчезнет этот объект. Никакими классическими физическими законами объяснить это будет нельзя. Во всех рассмотренных случаях объекты большей мерности (одно-, двух- и трехмерные) имеют нулевые условные проекции в нульмерном пространстве. Можно предположить, что эта закономерность справедлива для всех мыслимых пространств большей мерности. Одномерное пространство Как связаны друг с другом два смежных пространства – нульмерное и одномерное? Очевидно, что преобразование первого во второе производится принудительным добавлением координаты. В математике это описывается операцией интегрирования: то есть суммированием объектов по вновь введенной координате. Для получения следующего пространства мы просто директивно устанавливаем новую координату и присоединяем друг к другу по ней нульмерные пространства. При этом получаем одномерное пространство с единственной координатой x (название может быть любым). Никаких логических причин, кроме директивы, нет. Такое пространство мы можем изобразить уже в нашем реальном трехмерном пространстве в любом удобном для нас виде, например, на трехмерном кубе:  Рис.5 Одномерное пространство. В нем невозможно отобразить трехмерный объект, но нульмерный отображается однозначно. Здесь ось x является упомянутым вновь образованным одномерным пространством. Как видно из рисунка, в одномерном пространстве трехмерный объект – куб поместиться не может. Однако любой нульмерный объект отображается в этом пространстве вполне определенной величиной – координатой. Следовательно, нульмерное пространство имеет единственную проекцию в одномерном пространстве (то есть, координату). При перемещении одномерного объекта вдоль или поперёк одномерного пространства, он помещается в нём целиком и наблюдателю одномерного пространства он виден как цельный, со всеми своими свойствами, объект. В соответствии с принятыми правилами можно заметить, что по отношению к пространству большей мерности – двухмерному, трехмерному и так далее, наблюдаются такие же явления, как и для нульмерного пространства. Например, при пересечении одномерного пространства с двухмерным, наблюдатели одномерного пространства видят такое же удивительное явление: ниоткуда вдруг появляется объект одномерного мира, который совершенно необъяснимым образом изменяет свои свойства. Он может изменить свою длину, цвет, массу и даже просто исчезнуть в никуда:  Рис.6 При пересечении одномерного пространства двухмерным объектом, в одномерном пространстве появляется одномерная проекция. На рис.5 видно, как при движении двухмерного пространства (n=2) происходит наложение его с одномерным пространством (n=1). При этом двухмерное пространство (на рисунке это прямоугольник) вырезает на одномерной линии отрезок L. В зависимости от положения прямоугольника двухмерного пространства, длина этого отрезка может быть разной. Если прямоугольник движется, вращается, изменяет наклон к одномерной линии, длина отрезка будет изменяться строго в соответствии с этим движением (все движения - в плоскости двухмерного пространства). Причём для наблюдателя одномерного пространства будет неизвестна ни причина такого изменения, ни закономерность этого изменения, поскольку источник движения находится за пределами одномерного пространства. Аналогичная картина будет и при пересечении одномерного пространства трехмерным объектом:  Рис.7 При пересечении одномерного пространства трехмерным объектом, в одномерном пространстве появляется одномерная проекция. И в этом случае в одномерном пространстве появится новый одномерный объект длиной S. При этом для наблюдателя одномерного пространства нет никакой возможности определить, к какому «родительскому» пространству относится наблюдаемый объект: одномерному (с волшебными свойствами), двухмерному, трехмерному или более мерному пространству. При движении трехмерного объекта (n=3) сквозь одномерное пространство (линию n=1) наблюдатели последнего будут фиксировать различные свойства отрезка S: плотность, цвет, вязкость и другие, которые в общем случае для них будут изменяться по неизвестной причине, без закономерностей. Трехмерный объект может двигаться вдоль линии одномерного пространства или поперек него в двух возможных ортогональных направлениях, а также может вращаться вокруг любой оси. Все эти случаи проявляются в одномерном пространстве в изменении величины S и смещении этого отрезка вдоль оси одномерного пространства. Как отмечено, в одномерное пространство при этом «попадают» различные области трехмерного объекта, которые в общем случае могут иметь различные свойства. Как видим, первые два правила соблюдены, а третье правило вступит в силу, когда появится возможность сравнить два перехода от пространства к пространству (здесь мы имеем лишь один переход – от нульмерного к одномерному пространству). Двухмерное пространство Переход к пространству двух измерений производится в соответствии с третьим правилом так же, как и переход от нульмерного пространства к одномерному, то есть преобразование одномерного пространства в двухмерное производится принудительным добавлением координаты. Как отмечено, в математике это описывается операцией интегрирования - суммированием объектов по вновь введенной координате. Мы просто директивно устанавливаем новую координату и присоединяем друг к другу по ней одномерные пространства - линии. При этом получаем двухмерное пространство с двумя координатами x и y (названия могут быть любыми). Как и ранее, никаких логических причин, кроме директивы, нет. Как и в предыдущем случае, такое пространство мы можем изобразить в нашем реальном трехмерном пространстве в любом удобном для нас виде, например, на таком же трехмерном кубе:  Рис.8 Двухмерное пространство не позволяет отобразить трехмерный объект. Здесь ось y является вновь введенной координатой, приводящей к образованию двухмерного пространства xy. Как видно из рисунка, в этом двухмерном пространстве трехмерный объект – куб, как и в предыдущем случае одномерного пространства, поместиться не может. Зато в этом пространстве теперь вполне определенной величиной – координатами могут быть отображены объекты меньшей мерности – нульмерные (точка на плоскости xy) и одномерные (линия на плоскости xy). Объекты же трехмерные могут отобразиться в виде проекций. Например, при движении куба по третьей координате, он пересечёт плоскость двухмерного пространства и будет воспринят «наблюдателями» двухмерного мира как двухмерный объект – сечение трехмерного объекта плоскостью двухмерного пространства (проекция трехмерного объекта на плоскость двухмерного пространства xy):  Рис.9 При пересечении двухмерного пространства трехмерным объектом, в двухмерном пространстве появляется лишь двухмерная проекция. Как и в двух предыдущих случаях двухмерные наблюдатели смогут наблюдать странное явление: возникновение из ничего объекта их двухмерного мира, загадочное изменение его свойств, и такое же загадочное исчезновение объекта, если куб продолжит своё движение и в конечном счете выйдет за пределы плоскости этого двухмерного пространства. К загадочным изменяющимся свойствам объектов добавится площадь, которая будет изменяться при движении через двухмерное пространство трехмерного объекта, например, пирамиды. Любой объект большей мерности, чем две, будет отображаться в двухмерном пространстве в виде единственной проекции на плоскость xy. Трехмерное пространство Переход к пространству трех измерений производится в соответствии с третьим правилом так же, как и в предыдущих примерах принудительным добавлением новой, третьей координаты, что так же описывается в математике операцией интегрирования. Мы директивно присоединяем друг к другу по новой координате двухмерные пространства - плоскости. Получаем при этом привычное нам трехмерное пространство xyz без каких бы то ни было логических причин, кроме директивы:  Рис.10 Трехмерное пространство и трехмерный объект - куб. В этом пространстве теперь вполне определенной величиной – координатами могут быть отображены объекты меньшей мерности – нульмерные (точка на плоскости xy) и одномерные (линия на плоскости xy) и двухмерные (плоскости в пространстве xyz). Здесь мы можем предположить, что объекты большей мерности в полученном трехмерном пространстве могут отобразиться в виде трехмерных объектов (трехмерных проекций). Например, следует предположить, что при движении, скажем, четырехмерного куба по четвертой координате, он пересечёт объём трехмерного пространства и будет воспринят «наблюдателями» трехмерного пространства как трехмерный же объект – сечение четырехмерного объекта объемом трехмерного пространства (проекция четырехмерного объекта на объем трехмерного пространства xyz). Таким «сечением» или проекцией для трехмерного пространства может считаться любой объект, который мы наблюдаем в реальности. Видимо, при движении четырехмерного объекта по четвертой координате в нашем трехмерном мире должны наблюдаться такие же загадочные явления, какие описаны для пространств меньшей размерности. То есть, в пространстве может возникнуть из ничего некий объект, причём его свойства могут изменяться самым удивительным образом, ничем не объяснимым, с нарушением всех мыслимых законов физики. Например, объект может появиться из ничего, исчезнуть в никуда, может изменять свои размеры, массу, цвет и прочее. Изображение в трехмерном пространстве объектов меньшей мерности и наоборот было показано выше. Следует ожидать, что правила отображения в трехмерном пространстве объектов четырехмерного пространства должно подчиняться тем же правилам. В частности, эти четырехмерные объекты могут быть изображены в виде проекций на координатные плоскости. Поскольку пока не вполне ясно, как это произвести на практике, рассмотрим сначала собственно четырехмерные объекты. Четырехмерное пространство Переход к пространству четырех измерений произведём в соответствии с третьим правилом так же, как и в предыдущих примерах, принудительным добавлением четвертой координаты m, с учетом математической операции интегрирования. Мы директивно присоединим друг к другу по новой координате трехмерные пространства - объёмы. Однако, как это проделать в реальности, пока неясно. Видимо, при этом мы получим неочевидное пока четырехмерное пространство xyzm (без каких бы то ни было логических причин, кроме директивы). Как это изобразить на схеме? Для изображения четырехмерных объектов и исследования их поведения в трехмерном пространстве воспользуемся вышеприведенными правилами. Объекты в трехмерном пространстве можно изобразить в виде проекций на три пространственные плоскости. Для трехмерного мира этих плоскостей именно три. А сколько плоскостей в четырехмерном пространстве? Для трехмерного мира – это плоскости xy, xz, yz. В четырехмерном пространстве добавляется ещё одна координата. Поэтому следует предположить, что в таком пространстве есть четыре ортогональных оси: x, y, z, m. Как видим, эти четыре оси образуют 6 плоскостей проекций (двухмерных проекций): xy, xz, yz, mx, my, mz против 3 двухмерных проекций в трехмерном мире и одной – в двухмерном. Соответственно, возможны 4, 3, 2 и 1 (для одномерного пространства) одномерные проекции. Отсюда сразу же становится видна ещё одна категория проекций, характерная лишь для четырехмерного (и выше) пространства: трехмерная проекция. Такая проекция для четырехмерного мира, очевидно, может быть лишь одна – трехмерный объект. Рассмотрим простейшую четырехмерную фигуру – четырехмерный куб (тессеракт) в виде проекций на плоскости координат:  Рис.11 Двухмерные проекции четырехмерного куба. Нетрудно заметить полное сходство с проекциями в трехмерном пространстве. Отсюда и следует вывод: четырехмерный куб полностью аналогичен кубу трехмерному в изображении. В соответствии с третьим правилом, для четырехмерного пространства произведено «добавление», суммирование дополнительных элементов – объемов. В частном случае, если рассматривать пространство как дискретное (целочисленное), к исходному кубу (объему) прибавляются новые кубы. То есть, каждой дискретной координате m=1, 2, 3… и так далее соответствует свой собственный куб. Это разные кубы, имеющие каждый собственный набор свойств. Однако такое прибавление визуально осуществимо и в трехмерном мире, тогда в чем же разница? Разница в том, что каждый дополнительный объем находится вне трехмерного мира. Он невидим в трехмерном пространстве, вернее, всегда виден лишь один куб из набора. Если трехмерное пространство условно представить плоскостью, то трехмерные кубы-элементы «висят» над этой плоскостью. То есть такие кубы как бы соединены в своеобразную цепочку таким же образом, как были соединены плоскости при образовании объёма (объемного пространства). В четырехмерном же пространстве этот куб един, то есть по координате m мы можем изобразить лишь одну проекцию, один куб. Как этот куб просматривается с точки зрения пространства трехмерного? Поскольку куб имеет полностью совпадающие проекции, изобразим лишь одну из них, объединив как одинаковые три координаты xyz, и приняв за определяющую новую, четвертую координату:  Рис.12 При движении четырехмерного объекта по четвертой координате, в трехмерном пространстве могут возникнуть трехмерные проекции (тела), а могут и не возникнуть. Обозначение «x, y, z» у вертикальной оси просто отображает факт полного совпадения проекций xm, ym, zm. Как четырехмерный куб проецируется в трехмерное пространство? Очевидно, что все проекции четырехмерного куба в трехмерном пространстве являются, по крайней мере, кубом, изображенным в проекциях xy, xz, yz. То есть, перемещение четырехмерного куба в четвертом измерении по четвертой координате m не вызывает его перемещения по трём другим ортогональным координатам. Это наиболее простой и вместе с тем показательный, наглядный случай. Рассмотрим, что происходит в трехмерном пространстве при движении куба в общем, четырехмерном пространстве. Нас интересуют три точки: нулевая координата по оси m - 0, координата, попадающая в объём куба по этой координате, - А и координата, превышающая крайнюю точку куба – В. В тот момент, когда куб пересекает (касается) нулевой координаты, он как бы касается «плоскости» трехмерного пространства, то есть в трехмерном пространстве вдруг возникает объект – куб, изображенный проекциями xy, xz, yz. Визуально это означает появление, рождение в пространстве куба как бы из ничего. Происходит это потому, что при движении куба по оси m он касается осей x, y, z, то есть проявляет точки в этих координатах. Пересечение куба с осями создаёт на них точки. Дальнейшее движение куба по координате m не приводит ни к каким изменениям его трёхмерной проекции, если куб по этой координате m однороден. После пересечения кубом нулевой координаты m противоположной гранью, он исчезает для трехмерного пространства. Можно предположить, что объем четырехмерного куба равен произведению его граней: а4, а квадрат диагонали равен сумме квадратов его граней: 4a2. Четырехмерная пирамида может иметь следующий вид: 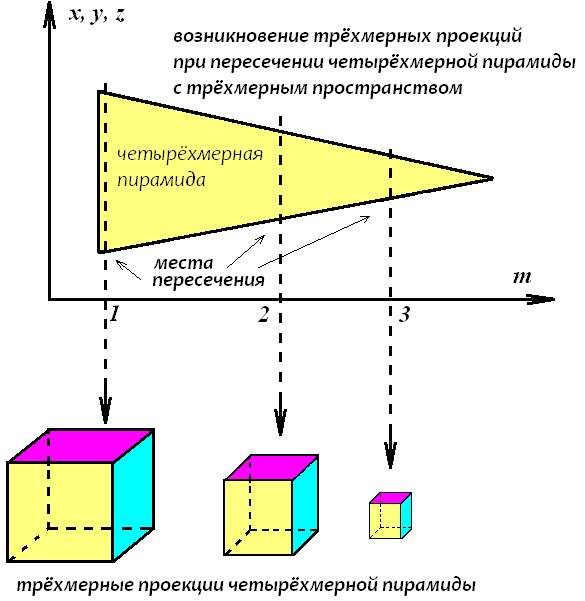 Рис.13 При движении пирамидального четырехмерного объекта (четырехмерной пирамиды) по четвертой координате, в трехмерном пространстве могут возникнуть трехмерные проекции (тела), величина которых зависит от сечения пирамиды по четвертой координате. При движении такой пирамиды через трехмерное пространство в нём будет наблюдаться изменяющийся по размерам куб. Сначала, когда пирамида коснётся пространства xyz, возникнут координаты трехмерного объекта куба размером, равным основанию пирамиды. Далее по мере движения пирамиды влево по рисунку размеры куба будут плавно уменьшаться и, наконец, когда пирамида коснётся вершиной пространства xyz, куб в этом пространстве исчезнет. Очевидно, что четырехмерная сфера, как и куб, должна иметь шесть одинаковых проекций:  Рис.14 Четырехмерная сфера в виде обобщённой трехмерной проекции (все проекции имеют одинаковый вид). При движении такой сферы сквозь трехмерное пространство (то есть по четвертой координате) – влево по рисунку – в трехмерном пространстве xyz будет наблюдаться сфера с изменяющимся радиусом. Таким образом, из всего сказанного можно сделать вывод, что четвертая координата фактически представляет собой «ось», на которую «нанизаны» трехмерные объекты. Перемещение по этой оси приводит, в определенном смысле, к поочередному появлению в трехмерном пространстве нанизанных на неё объектов. В частности, можно нанизать на такую ось «яйце - куриные» объекты:  Рис.15 Сложный четырехмерный объект «Эволюция яйца». По четвертой координате даны дискретные обобщенные изображения (трехмерные проекции). На самом деле четырехмерный объект является монолитным, и между двумя соседними проекциями пространственных разрывов нет. При движении по четвертой координате такого «яйце-куриного объекта» в трехмерном пространстве будет наблюдаться эволюционное преобразование «яйцо – цыпленок – курица». Широко распространенным примером четырехмерного пространства можно признать скринсэйвер (хранитель экрана) «Метаморфозы» в операционной системе Windows:  Рис.16 Сложный четырехмерный объект – скринсэйвер ОС MS Windows «Метаморфозы». По четвертой координате даны дискретные обобщенные изображения (трехмерные проекции). На самом деле четырехмерный объект является монолитным, и между двумя соседними проекциями пространственных разрывов нет. Этот объект фактически представляет собой последовательность форм, проявляющихся в условном трехмерном (3D) пространстве экрана монитора при движении его через это пространство по четвертой координате. Движение может быть дискретным, тогда четырехмерный объект представляет собой последовательность трехмерных объектов. Наиболее простым и ярким представителем такого четырехмерного объекта можно считать киноленту. Каждый кадр её – это дискретный элемент (трехмерная проекция) четырехмерного объекта, а передвижение ленты через проектор – это перемещение по четвертой координате, в результате чего в трехмерном пространстве отображаются кадры киноленты (трехмерные проекции). Если кадры сделать достаточно подробными, частыми, то, устремив в пределе к нулю разницу между двумя соседними кадрами, можно получить непрерывный (сплошной) четырехмерный объект. Упрощенно явление движения четырехмерного объекта с дискретным превращением, переходом от одной трехмерной проекции к другой (метаморфозы) можно изобразить следующей схемой:  Рис.17 Сложный четырехмерный объект – метаморфозы куба в эллипосоид. По четвертой координате даны дискретные обобщенные изображения (трехмерные проекции). На самом деле четырехмерный объект является монолитным, и между двумя соседними проекциями пространственных разрывов нет. Здесь показано движение точки А в процессе изменения координаты m. На рисунке условно принято, что объект по двум трёхмерным координатам, например, y и z симметричен, то есть его проекции на эту плоскость - это квадрат, ромб, круг, в то время как на две другие плоскости (xy и xz) - прямоугольник, вытянутый ромб, овал. Весь объект в целом в трёхмерном пространстве преобразуется при движении по четвертой координате дискретно (скачками) из куба в эллипсоид. Другими словами, в трёхмерном пространстве наблюдатели будут видеть изначально небольшой голубой кубик, который в одно мгновение превращается в большой зелёный ромб, ещё через некоторое время мгновенно превращается в жёлтый кристалл и, наконец, в сильно вытянутый синий эллипсоид. Ещё раз подчеркнем, что этот объект в реальности вполне может быть монолитом, а не упрощённым набором изображённых на схеме отдельных фигур. Действительно, с некоторой степенью условности этот объект можно изобразить непрерывным (рис.18) -криволинейной пирамидой. Координаты 1 - 4 по оси m на рис.18 соответствуют фрагментам, слоям, сечениям этой пирамиды. Таких слоёв, сечений бесконечное множество и все они, как отмечалось, 'нанизаны' на ось m. Как видно на рис.18 по вертикальной оси m можно получить не только приведённые выше дискретные слои с координатами m=1, 2, 3, 4 (выделенные цветом слои - сечения), но и любое промежуточное значение. Как принято в данной статье, для наглядности, на рисунке показаны две традиционные пространственные координаты x, y и четвертая координата m. Третьей пространственной координате на рисунке может быть, например, присвоено фиксированное значение z=h. В этом случае каждое из трёхмерных сечений четырёхмерного объекта (криволинейной пирамиды) будет представлять собой 'блин' высотой h: сверху блин-квадрат, снизу - блин-овал. Такие 'блины', конечно, можно 'разглядеть' и на рисунке 18, однако, не нужно забывать, что высота блина - это его измерение по координате z, а не по координате m, как может показаться из рисунка. 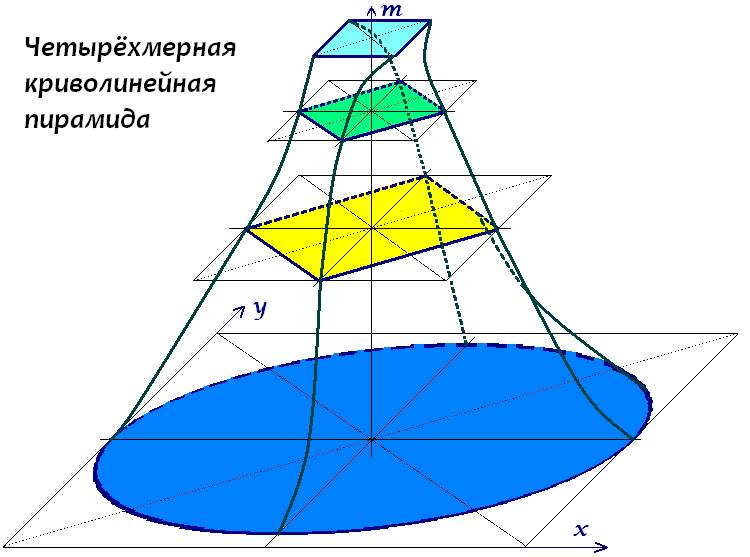 Рис.18. Сложный четырёхмерный объект - непрерывная криволинейная пирамида, представляющая собой метаморфозы куба в эллипсоид или метаморфозы 'блинов'. При такой сплошной конфигурации четырёхмерной криволинейной пирамиды, она будет 'давать' при движении по четвёртой координате m трёхмерные сечения в виде квадратного, ромбического и овального блинов. Причём в этом случае изменения трёхмерных форм объектов будут уже плавными, а не скачкообразными, как было в первоначальном варианте с дискретными значениями 'слоёв'. Как правило, любое перемещение объектов по координатным осям связано с течением времени. То есть собственно перемещение зависит от времени. Однако, эта зависимость необязательна, она просто удобна. Очевидно, что время при этом относится одинаково к любой из четырех координат, само при этом не являясь пространственной координатой. Следует особо отметить, что набор трехмерных компонент (трехмерных проекций) четырехмерного объекта может быть произвольным. Например, для некоторого дискретного четырехмерного объекта можно использовать набор оловянных солдатиков. Каждый шаг по оси четвертого измерения будет отображать, «рождать» в трехмерном пространстве нового солдатика взамен предыдущего. Еще раз отметим: поскольку все координаты четырехмерного пространства являются ортогональными, то перемещение по четвертой координате не приводит к изменению положения трехмерного объекта в пространстве координат X-Y-Z. Перемещение по четвертой координате вызывает изменение формы, структуры объекта или каких-либо других его свойств, причём удивительным образом, как если бы объект делал это самопроизвольно, без участия кого-либо, без каких бы то ни было воздействий на него изнутри трехмерного пространства. Существует ли возможность изобразить четырехмерную ортогональную систему координат в трехмерном пространстве? Видимо, да. Ведь в двухмерном пространстве похожая возможность имеется: аксонометрические изображения в соответствии с общепринятыми соглашениями по изображению трехмерных объектов на двухмерной плоскости. Для четырехмерной аксонометрии необходимо помнить, что изображение должно быть в трехмерном пространстве, а не на двухмерном пространстве бумаги. То есть мы наносим традиционные три оси аксонометрии на бумагу и ставим четвертую ось – карандаш, перпендикулярно этому листу. Теперь мы имеем реальные четыре оси, между которыми образованы проекционные плоскости, и такую конструкцию – четырехмерную аксонометрию – мы в принципе можем изобразить на таком же листе (хотя и потребуется изрядная доля воображения). Для этого по новой, четвертой оси мы будем откладывать «срезы» трехмерных аксонометрий четырехмерного пространства. Чем чаще расположены срезы, тем точнее четырехмерная аксонометрия. Для построения примера такой аксонометрии возьмём в качестве объекта простейший из них - четырехмерный куб, который имеет следующие трехмерные проекции (на рисунке показана одна из одинаковых шести проекций):  Рис.19 Трехмерный куб как частная трехмерная проекция четырехмерного куба. Эти трехмерные проекции «нанизываем» на четвертое измерение и получаем аксонометрию четырехмерного куба в четырехмерном пространстве:  Рис.20 Четырехмерный куб (тессеракт) представленный в виде дискретных частных трехмерных проекций, «нанизанных» на четвертую координату. В целом четырехмерный куб является монолитным, и между двумя соседними трехмерными проекциями пространственных разрывов нет. Здесь принято, что этот куб неподвижен по всем четырем координатам. Отсутствие движения, позволило показать на рисунке дискретные значения проекций для некоторых произвольных значений четвертой координаты 0, 1, 2, 3, 4. Перекрытие слоёв (проекций) показано штриховыми линиями лишь для значения m=3, чтобы не загромождать рисунок. Напомним, что в реальности все фигуры (проекции) в четырехмерном пространстве являются монолитом, то есть в нём нет такого явного разделения на слои (проекции). Однако не следует думать, что четырехмерный куб при этом является скорее своеобразной «колбасой», чем «железнодорожным составом» из отдельных трехмерных кубиков, которые просто присоединены друг к другу. Другой пример четырехмерного объекта, который можно назвать «38 попугаев», изображен на следующем рисунке: 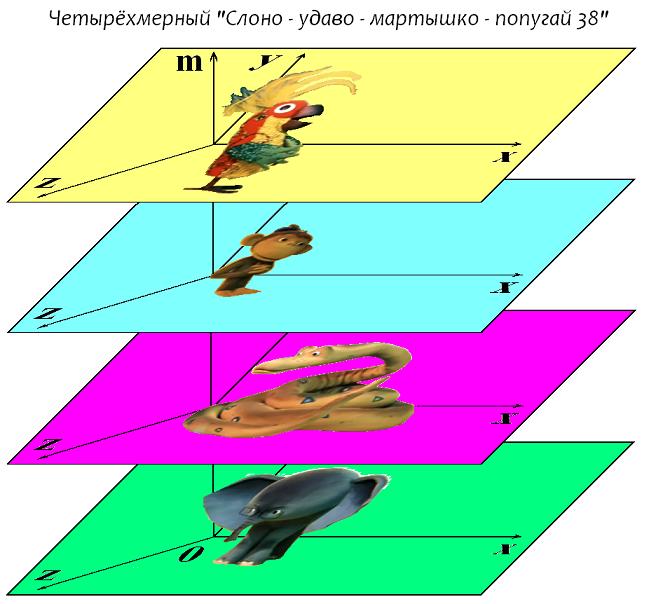 Рис.21 Четырехмерный объект «38 попугаев», представленный в виде дискретных частных трехмерных проекций, «нанизанных» на четвертое измерение (координату). В целом четырехмерный объект является монолитным, и между двумя соседними трехмерными проекциями не пространственные разрывы, а специфические «слоно-удав», «удаво-мартышка» и «мартышко-попугай». Хотя приведены лишь четыре дискретные трехмерные проекции объекта, нужно понимать, что между ними есть связующие «звенья» - метаморфозные преобразования, в которых находятся промежуточные состояния изображенных проекций, например, «слоно-удав» или «мартышко-попугай». Пятимерное пространство и пространства большей мерности Добавим к четырехмерному пространству новое, пятое измерение k. В полученной системе, очевидно, появились 4 новые плоскости проекций kx, ky, kz и km. Такой пятимерный куб будет иметь, очевидно, следующие десять двухмерных проекций:  Рис.22 Двухмерные проекции пятимерного куба В трехмерном пространстве проекции могут быть кубами и в том случае, если по двум высшим измерениям (четвертой и пятой) объект не только не является кубом, но может быть вообще фигурой произвольной сложности. Подобный случай можно изобразить схематически в трехмерной аксонометрии путем группировки равных измерений, как это было сделано выше: 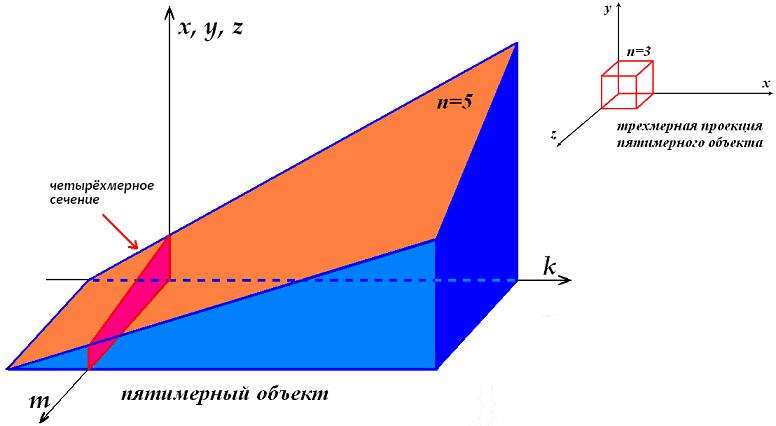 Рис.23 Четырехмерный клинообразный объект в виде обобщённой трехмерной проекции (все трехмерные проекции имеют вид куба) При движении такого пятимерного объекта по любой из высших координат в трехмерном пространстве будут возникать и исчезать трехмерные кубы различной величины и с различными свойствами. Эти свойства определяются свойствами объекта в целом. Например, по одной из координат m – объект имеет различную плотность, а по другой k – различный вещественный состав. Для наблюдателя трехмерного пространства будет происходить явление, не поддающееся описанию с физической точки зрения: куб может запросто превратиться из свинцового в золотой. Всё изложенное позволяет свести набор пространственных координат в своеобразную схематичную иерархию – аналогию с привычными окружающими нас объектами. В качестве нульмерного пространства а) в реальном мире мы можем рассматривать как точку, так и с долей условности любой мелкий объект – шарик, зёрнышко и так далее. С одномерным пространством б) можно ассоциировать любой протяженный тонкий предмет – струну, лыжную палку и прочее. Все плоские двухмерные объекты в) – это картины, чертежи, плакаты, которые мы условно изобразим в виде кадра киноленты. Примеров трехмерных пространств г) ещё больше: это, по существу, все окружающие нас предметы. 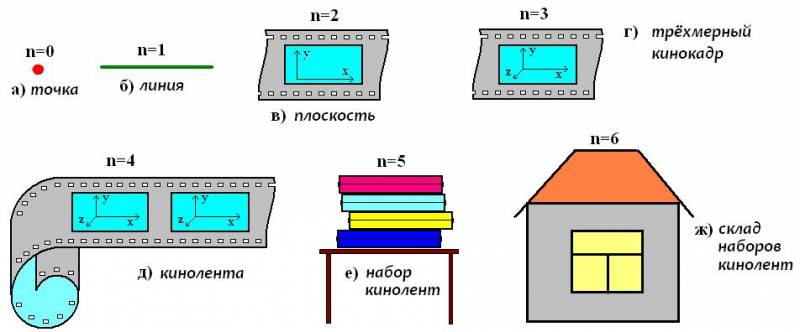 Рис.24 Ассоциативное представление последовательности пространств различной мерности Однако для общности дальнейшего изложения, трехмерные пространства г) на рисунке мы изобразим как и двухмерные пространства – в виде аксонометрий (3D – объектов), запечатлённых на кадре киноленты. В этом случае сама кинолента может уже рассматриваться как четырёхмерное пространство д). Каждый кадр киноленты при этом является отдельной трехмерной проекцией г). Чем чаще кадры фиксируют окружающую действительность, тем более точно они изображают четырехмерное пространство. Понятно, что перемещение по четвертой координате пространства соответствует движению киноленты в киноаппарате. Причём мы свободны в нашем выборе: можно ленту двигать быстрее, можно медленнее, можно вообще её остановить и даже прокрутить в обратную сторону. В этом смысле время в качестве четвертой координаты не даёт нам практически никакого выбора. Если кинолента может быть ассоциирована с четырехмерным пространством, то набор кинолент, шкаф с кинолентами е) можно ассоциировать с пятой координатой. Разумеется, при такой аналогии все координаты являются дискретными и связь между различными состояниями объекта прерывистая, не плавная. В качестве следующей ассоциации – шестимерного пространства – можно привести склад с шкафами кинолент ж). Можно было бы продолжить аналогии многомерных пространств, но ничего нового это уже не даст. Более того, уже на этом этапе видна любопытная закономерность. Если мы предположим, что многомерные пространства существуют в реальности, хотя и в более сложном, непрерывном, монолитном виде, то здравый смысл и логика сразу же зададутся вопросом: а почему мы, собственно говоря, не наблюдаем в повседневной жизни никаких из описанных свойств таких многомерных пространств? Ведь если они действительно существуют, то эти необъяснимые явления должны себя хоть как-то проявлять. Или всё же какие-то из загадочных явлений мы можем отнести к проявлениями движения четырёхмерных объектов через наше трёхмерное пространство? Что можно сказать, например, об НЛО? Или о загадочных кругах и других фигурах, образованных утрамбованными стеблями трав на полях и лугах? А неопознанные плавающие объекты - НПО - светящиеся и вращающиеся фигуры на морской поверхности (''дьявольская карусель'')? Это ли не явное проявление четырёхмерной проекции? Или, наконец, весьма ''ощутимое'' хорошо известное явление - шаровая молния? Вряд ли можно на эти вопросы ответить утвердительно. Конечно, один из основных признаков описанных явлений, казалось бы, совпадает с характерным признаком четырёхмерного объекта, спроецированного на трёхмерное пространство - появление его из ничего и такое же загадочное исчезновение. Однако, этот признак в целом для объектов не так уж и значителен, да и не надёжен - всегда можно привести более реалистичные причины возникновения и исчезновения. Существеннее другое - быстрое перемещение в пространстве, вращение, явная зависимость от среды, где явление отображается, что совсем не свидетельствует в пользу четырёхмерности. Если это и проекция четырёхмерного объекта, то он находится в весьма сложном движении в своём четырёхмерном пространстве, причём движется главным образом по трём воспринимаемым нами пространственным координатам. Другими словами, объяснение загадочных явлений четырёхмерностью пространства слишком искусственно, не убедительно. Следовательно, вряд ли разумно принимать реальность наличия четвёртой пространственной координаты. Пространства большей мерности, в прямом понимании пространственности координат, выглядят ещё менее убедительно. Литература 1. Путенихин П.В., Материя, Пространство, Время. 2007, URL: http://samlib.ru/p/putenihin_p_w/materia.shtml (дата обращения 29.12.2015) 2. Путенихин П.В., Свойства эфира, 2008, URL: http://samlib.ru/editors/p/putenihin_p_w/ephir.shtml (дата обращения 29.12.2015) 3. Путенихин П.В., Трехмерность бытия и теоремы Ферма и Пифагора, 2004, URL: http://samlib.ru/editors/p/putenihin_p_w/pifagor.shtml (дата обращения 29.12.2015) 25.06.2010 Адрес полного текста статьи в интернете URL: http://samlib.ru/p/putenihin_p_w/mnogomer.shtml Иллюстрации и уравнения к статье (зеркала) http://samlib.ru/p/putenihin_p_w/ https://cloud.mail.ru/public/8WpP/qeaUMAiGz https://cloud.mail.ru/public/Hq7e/jZ9YZGJW9 https://yadi.sk/d/EZg36rrKmJDwk https://drive.google.com/folderview?id=0B0uM56-EnG4ZaUFJb0YzY3YtcVU&usp=drive_web http://fileload.info/users/putenikhin/ | |
| Категория: Разное | | | |
| Просмотров: 3974 | Загрузок: 84 | |
| Всего комментариев: 0 | |