Путенихин П.В. Итак, парадокса (близнецов) больше нет! - Разное - Публикации - Каталог научных статей

Путенихин П.В. Итак, парадокса (близнецов) больше нет!

[ Скачать с сервера (4.39 Mb) ]	10.02.2016, 10:24
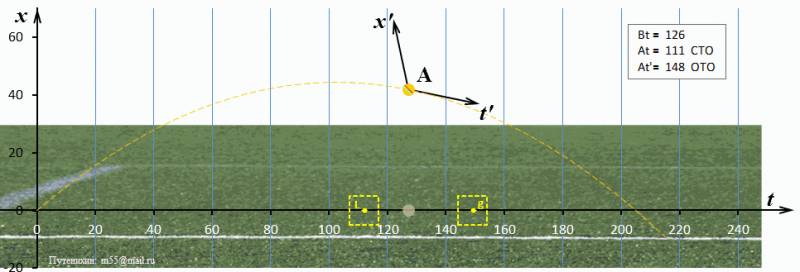
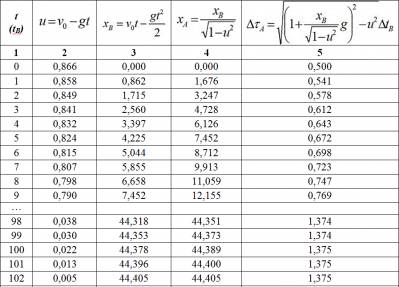
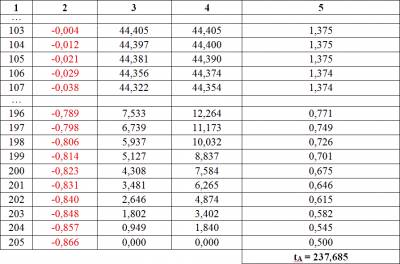
Итак, парадокса (близнецов) больше нет! П.В.Путенихин m55@mail.ru Аннотация Названием статьи взята фраза из книги Л.Мардера «Парадокс часов». Распространено мнение, что в общей теории относительности парадокс близнецов не является парадоксом, а имеет четко обоснованное решение. В статье анализируется один из вариантов такого решения с использованием динамических диаграмм Минковского. В качестве названия предлагаемой статьи я взял фразу из книги Лесли Мардера «Парадокс близнецов» (с.199). В английском оригинале фраза звучит так: The paradox no longer exists. Как известно, парадокс близнецов берёт своё начало в основополагающей работе по теории относительности – работе Эйнштейна 1905 года «К электродинамике движущихся тел». В данной работе мы не рассматриваем предысторию парадокса, его формулировки и многочисленные варианты его решений. Также мы не подвергаем критике или сомнению утверждение о том, что в общей теории относительности, действительно, «парадокса больше нет». Мы лишь рассмотрим в общих чертах выкладки, которые можно отнести к релятивистскому решению парадокса. Следует особо отметить, что парадокс имеет решение только в общей теории относительности. Напротив, специальная теория относительности не позволяет его разрешить, парадокс не является задачей специальной относительности. Эту позицию четко сформулировал Розман: «При изучении СТО указывается, что «парадокс близнецов» не может быть объяснен в рамках этой теории. … Этот парадокс не может быть разрешен в рамках СТО, так как рассматриваемые СО не равноправны (как это требуется в СТО): космический корабль не может рассматриваться ИСО, так как движется на отдельных участках траектории неравномерно. Только в рамках ОТО мы можем понять и объяснить «парадокс близнецов» естественным образом, опираясь на положения OТО» [Розман, 2005, c.220]. Опуская промежуточные выкладки, приведу заключительное уравнение, с помощью которого и выводится это решение: 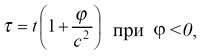«из которой ясно видно, что темп хода часов замедляется в гравитационном поле с потенциалом φ (то же справедливо и для эквивалентной ускоренно движущейся СO, каковой в нашей задаче является космический корабль с «близнецом» «В»). Таким образом, часы на Земле покажут больший промежуток времени, чем часы на космическом корабле при его возвращении на Землю» [Розман, 2005, с.220]. К сожалению, Розман не приводит развёрнутых выкладок, делая лишь риторическое, но весьма показательное заключение: «Повторим еще раз, что «парадокс близнецов» не имеет никакого объяснения в специальной теории относительности, в которой используются только равноправные инерциальные CO. Пo СТО «близнец» «В» должен вечно равномерно и прямолинейно удаляться от наблюдателя «А» (по сути дела, он не должен взлетать с Земли, именно поэтому мы берем слово «близнец» в кавычки). В популярной литературе часто обходят «острый» момент в объяснении этого парадокса, заменяя физически длящийся разворот космического корабля «назад к Земле» его мгновенным разворотом, что невозможно. Этим «обманным маневром» в рассуждениях устраняют ускоренное движение корабля на развороте и тогда обе СО («Земля» и «Корабль») оказываются равноправными и инерциальными, в которых можно применять положения CTO. Но такой прием нельзя считать научным» [Розман, 2005, c.220]. Можно ли сказать лучше? Вряд ли. Эту очевидную, по сути, мысль следовало бы принять к сведению не только всем противникам специальной теории относительности, антиСТО, но и её убеждённым сторонникам, поскольку и первые, да и многие из вторых по-прежнему пытаются решать «парадокс близнецов» средствами специальной относительности. Здесь же, у цитированного автора мы видим основное направление решения парадокса: «В заключение следует отметить, что «парадокс близнецов» является, по сути дела, разновидностью того эффекта, который был разобран … и назывался изменением частоты излучения в гравитационном поле» [Розман, 2005]. Должен сказать, что мои попытки найти собственно решение парадокса часов в рамках общей теории относительности принесли достаточно скромный результат. Из многих десятков просмотренных мною учебников, статей и рефератов лишь одна содержала подробное решение этого парадокса – книга Скобельцына «Парадокс близнецов в теории относительности» [Скобельцын, 1966]. С выкладками в книге следовало бы ознакомиться, а лучше тщательно проанализировать и изучить всем, кто ищет решение парадокса близнецов и, особенно, ищет в парадоксе признаки ошибочности теории относительности. Однако, решение Скобельцына относится к довольно фантастическому варианту парадокса с нефизическими значениями параметров: мгновенным разворотом и бесконечно большим ускорением при развороте. Тем не менее, решение следует признать достаточно корректным. В предлагаемой работе, тем не менее, мы попробуем получить такое же решение, но уже с реально достижимыми значениями ускорений и времени разворота. Сначала обратим внимание на очевидное обстоятельство в процессе движения сравниваемых часов (в системах отсчета близнецов): «… если рассматривать ситуацию, возникающую при осуществлении цикла движений с «путешествующим» в космосе В и остающимся «неподвижным» на Земле его близнецом А, то имеет место следующее: когда в середине путешествия В направление скорости его (В) изменяется на противоположное и в некоторый момент времени он начинает сближаться с А, то в течение того времени, когда он, находясь на большом расстоянии от А, движется в направлении к А ускоренно, ему (B), считающему себя неподвижным, представляется, что течение процессов в системе А убыстряется». [Скобельцын, 1966, с.167] Это убыстрение времени совершенно очевидно, поскольку, если по итогам совместного движения одни часы отстали, то нет и не быть может другого заключения: вторые из этих часов шли быстрее! При выводе своего решения автор делает ссылку на предшественника: «нижеследующие выкладки в значительной части представляют собой «парафразу» в упрощенном виде выводов, содержащихся в книге Меллера [Мёллер, 1975], рассмотревшего впервые … в достаточно общем виде вопрос о «парадоксе часов» с точки зрения общей теории относительности» [Скобельцын, 1966]. Хочу отметить, что выкладки Скобельцына являются более конкретными и последовательными, чем у Меллера, который в работе по указанной ссылке приводит лишь основные, хотя и важные, тезисы для решения парадокса, а самого развернутого решения, собственно говоря, я не увидел. В том или ином виде решение парадокса близнецов в общей теории относительности, как сказано выше, опирается на так называемое «гравитационное красное смещение» и принцип эквивалентности. Мардер описывает эту картину следующим образом: «Всякий раз, когда действовало ускорение, вызванное работой двигателей, М мог считать, что двигатели удерживают его в состоянии покоя в однородном гравитационном поле — это соответствует принципу эквивалентности. Так как у наблюдателя R двигателей нет, он свободно падает в этом гравитационном поле. … Но часы, помещенные в область с повышенным значением гравитационного потенциала, должны спешить…» [Мардер, 1974, c.199]. Здесь наблюдателей М и R можно назвать двумя близнецами рассматриваемого парадокса. Описанная картина означает, что второй из близнецов, улетавший на корабле в космос, в момент разворота оказывается в эквивалентном гравитационном поле. То есть, хотя на самом деле он и не находится вблизи какого-либо массивного гравитирующего тела, но согласно принципу эквивалентности теории относительности мы можем с полным правом рассматривать его находящемся именно вблизи такого тела. Условно говоря, космический корабль является как бы массивной планетой, создающей гравитационное поле такой напряжённости, что ускорение свободного падения на ней в точности равно ускорению, создаваемому двигателями корабля при его развороте. Напомню, что самым высоким гравитационным потенциалом, а точнее, нулевым обладает область полностью свободная от массивных, гравитирующих тел. В нём часы идут с наибольшей скоростью (темпом). Поскольку ко второму близнецу, находящемуся на Земле, не приложены никакие силы, он тоже может рассматриваться как находящийся в гравитационном поле корабля. Однако, здесь следует сделать оговорку. Второй близнец, землянин находится в гравитационном поле Земли. Для простоты мы считаем, что в рассматриваемом случае масса Земли равна нулю, то есть влиянием её гравитационного поля мы пренебрегаем. Это вполне допустимо, поскольку второй близнец мог находиться вовсе и не на Земле, а на небольшой космической станции с пренебрежимо малой массой. Таким образом, этот второй близнец находится в эквивалентном гравитационном поле космического корабля и под его действием совершает «свободное падение» на корабль. Согласно общей теории относительности и в соответствии с релятивистским явлением «гравитационного красного смещения» все часы, удалённые от центра корабля идут в более быстром темпе, спешат. Изменение этого темпа хода часов и даёт уравнение общей теории относительности [Скобельцын, 1966]: (1) где: dτ, dt - интервалы времени, прошедшие по часам, соответственно, на «падающем» (Земля) и на гравитирующем теле (космическом корабле); x - расстояние между телами (между близнецами); понятно, что она зависит от времени, поскольку «падение» земного брата в «гравитационном» поле брата-космонавта происходит с ускорением; g(t) - ускорение свободного падения на гравитирующем теле; u - скорость падения или относительная скорость близнецов; понятно, что она зависит от времени, поскольку «падение» земного брата в «гравитационном» поле брата-космонавта происходит с ускорением; χ - так называемый, гравитационный потенциал, создаваемый «гравитационным» полем корабля при его развороте в точке пространства, в которой находится земной брат; также очевидно, что значение потенциала зависит от расстояния между близнецами и, соответственно, величины ускорения корабля в этой точке. Нас не должны интересовать промежуточные выкладки, на основании которых получено это уравнение. Его приводят разные авторы как основное уравнение, являющегося как описанием гравитационного красного смещения, так и решения парадокса близнецов. В этом уравнении мы видим, в чем, собственно, и состоит сущность решения парадокса близнецов в общей теории относительности. С одной стороны, в процессе сближения братьев и увеличения их относительной скорости часы земного брата замедляются. Это соответствует специальной теории относительности и является причиной возникновения парадокса. Однако, с другой стороны, эквивалентный «гравитационный» потенциал корабля приводит к противоположному эффекту: он вызывает ускорение хода земных часов. В сумме оба эффекта должны привести к тому, что показания часов земного брата в момент встречи будут больше показаний часов улетавшего брата, как того и требует корректное решение парадокса близнецов. Получается, вопреки специальной теории относительности, что движущиеся часы (часы земного брата) идут быстрее, чем неподвижные (часы на корабле). Эти обобщенные рассуждения мы попробуем теперь воплотить в графическом, числовом виде на динамических диаграммах Минковского. Следом за диаграммами я буду давать максимально подробное их описание. 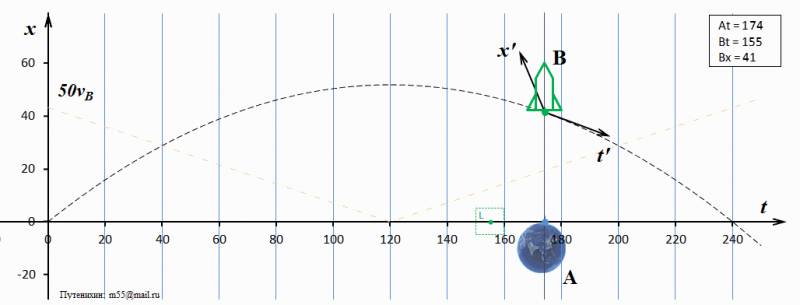Рис.1 Диаграмма Минковского – релятивистское решение «парадокса близнецов». Картина с точки зрения земного близнеца А. На предлагаемых диаграммах Минковского я поменял местами ось времени ct и ось расстояний x. Это не новый приём, им пользуются и другие авторы. В данном случае такое расположение осей удобно, поскольку делает картину более естественной и наглядной. Как видим, корабль взлетает строго вертикально вверх и затем опускается так же сверху на Землю. Можно заметить, что эта картина полностью совпадает с задачей классической физики о броске камня вертикально вверх. Систему отсчёта земного брата обозначим буквой А, а систему отсчета корабля – буквой В. Штриховой параболической линией ветвями вниз изображена мировая линия космического корабля. Точкой и короткими осями t'-x' изображена система координат, связанная с кораблем: здесь хорошо видна основная особенность диаграмм Минковского - косоугольные оси координат движущихся объектов. Оси t-x относятся к системе отсчета Земли. Вертикальная линия, соединяющая корабль и Землю – это линия «настоящего» (время) в системе отсчета Земли. Эта диаграмма является базовой, исходной. На ней мы видим исходные, заданные нами параметры движения. Угол наклона мировой линии корабля в начале и конце пути имеет тангенс, равный скорости корабля при отлёте от Земли и при его возвращении. Мировая линия корабля пересекает мировую линию Земли в двух точках – нулевой и 240 месяцев, являющихся временами начала и окончания полёта корабля. Приведённая диаграмма относится к системе покоя условно неподвижного близнеца – на Земле. Однако, в парадоксе близнецов нас в первую очередь должна интересовать картина, какую наблюдает улетавший брат. Действительно, с точки зрения земного, неподвижного брата ситуация предельно ясна. Она полностью и корректно описывается математикой специальной относительности и даёт исходные данные для последующих расчетов. Для удобства этих последующих расчетов мы приняли: 1. Начальная скорость корабля 0,866с или 259 628 км/сек; 2. Интервал времени, на котором исследуется парадокс, равен 240 месяцам; 3. Величина ускорения разворота неизменна на всём протяжении полёта. Этих трёх условий достаточно, чтобы вычислить все остальные параметры. Действительно, начальная скорость означает, что в момент начала удаления близнецов корабль уже имеет начальную скорость, тормозные двигатели включены и корабль движется с фиксированным ускорением разворота. Мы постулируем, что корабль приобрёл эти параметры движения до первой встречи близнецов и нам нет необходимости учитывать переходные процессы. В момент их второй встречи при возвращении через 240 месяцев, корабль будет иметь точно такую же скорость, поскольку ускорение неизменно. Время полёта, равное 20 годам, мы взяли произвольно просто из соображений «круглости» и учета, что это наглядный возраст близнецов. По начальной скорости и времени полёта можно легко вычислить ускорение разворота (торможения). Замечу, что особенностью построения диаграмм является их интервальность, то есть все графики являются на самом деле не сплошными кривыми, а ломаными. В точности с формулировкой Эйнштейна. Таким образом, в нулевой точке начала отсчета скорость корабля равна 0,866 и далее она снижается. В конечной точке, в момент встречи близнецов, скорость корабля также достигает этой скорости (со знаком минус). Уравнение движения корабля с точки зрения землянина в этом случае имеет вид: (2) где: v_B – текущая скорость корабля; v₀ – начальная скорость корабля, равная 0,866; а – искомое ускорение торможения корабля. t_A – время полёта корабля от встречи до встречи, равное 240 месяцам. Как мы приняли, в момент второй встречи скорость корабля будет такой же, но с противоположным знаком: Откуда: (3) Значение скорости корабля 0,866 взято как округленное значение дроби √3/2. Следовательно, из заданного условия времени tA движения корабля по часам Земли, равным 240 месяцев, находим ускорение разворота (торможения): Поскольку мы взяли значение скорости света, равное единице, то и ускорение мы получили в схожих единицах измерения. Если перевести ускорение в обычные единицы, то мы получим величину, почти в 11 раз меньшую ускорения свободного падения на Земле: Таким образом, по истечении 240 месяцев, корабль, движущийся с отрицательным ускорением 0,007 и начальной скоростью 0,866, вернётся на Землю, имея скорость минус 0,866. Эти условия, как указано выше, позволяют нам исключить из рассмотрения не только начальный этап разгона и конечный этап торможения, но и моменты изменения ускорения при развороте. Действительно, ускорение связано с приложением к кораблю некоей силы. Эта сила не может быть приложена и снята мгновенно, поэтому следовало бы учитывать и этапы нарастания и уменьшения не только скорости корабля, но и его ускорения. Кроме того, в дальнейшем нам будет проще учитывать эффект гравитационного красного смещения, поскольку постоянное ускорение означает и постоянное эквивалентное гравитационное поле корабля – его «гравитационный» потенциал. В соответствии с приведённым уравнением движения можно найти удаление, путь, пройденный кораблем в системе координат Земли: (4) Подставляя в него полученное значение ускорения разворота (3) и начальную скорость корабля, получаем уравнение его движения в системе Земли: После подстановки заданных условиями задачи числовых значений, получаем уравнение: (5) Именно это уравнение (5) было использовано для построения мировой линии корабля как функции расстояния от времени полёта на приведённой на рис.1 диаграмме Минковского. Нам также известно, что время на корабле течёт медленнее, чем на Земле, поэтому мы можем по уравнению движения корабля вычислить темп хода времени на нём и, соответственно, время в пути по часам корабля: Подставляя в уравнение исходные данные, находим интегрированием время в пути по часам корабля: После подстановки числовых значений заданных условиями задачи, получаем уравнение для показаний часов на корабле с точки зрения Земли: (6) Показания часов корабля в соответствии с функцией (6) изображены на диаграмме рис.1 в виде индикатора - штрихового квадрата, помеченного буквой L (лоренцево замедление времени). В процессе полёта корабля видно, что этот индикатор отстаёт от линии настоящего. В конце полёта индикатор показывает время (в нашем примере) – 205 месяцев. Это и есть возраст улетавшего брата - t_B, каким он будет в момент встречи близнецов. Однако, следует упомянуть об одном упрощении. Мы посчитали возраст космонавта без учета того, что он двигался в условиях гравитационного поля. На самом деле в этом случае его возраст должен быть ещё меньше, ведь часы на корабле имели не только лоренцево замедление, но и замедление вследствие действия гравитации. То есть, возраст земного брата в этом случае должен быть ещё больше по сравнению с возрастом космонавта. Но ниже мы увидим, что возникает некоторое отклонение, которое существенно превышает эту не учтенную нами поправку. Итак, картина, которую наблюдают с Земли, вполне корректна и не вызывает никаких возражений по существу. Строго в соответствии с формализмом специальной относительности улетавший брат оказывается моложе брата, остававшегося на Земле. Но парадокс состоит в том, что по отношению к улетавшему брату неподвижным был космический корабль, а двигался земной близнец. Поэтому, казалось бы, моложе должен был оказаться брат на Земле. Но это не так. Согласно общей теории относительности, ускоренное движение корабля привело к тому, что с точки зрения корабля часы на Земле шли ускоренно. Эта ситуация изображена на диаграмме Минковского рис.2. На ней неподвижной системой отсчета является система корабля, а движется Земля. Параболическая штриховая линия на диаграмме является мировой линией Земли в системе отсчета корабля. Я не стал изображать на диаграммах традиционные мировые линии света. Вместо них я изобразил линией бледно-малинового цвета график скорости Земли с точки зрения корабля. Она обозначена как 50v_A, то есть её масштаб увеличен в 50 раз, иначе линия будет практически сливаться с осью t'. Видим, что «скорость» Земли остается неизменной на всём протяжении полёта корабля. Как и на предыдущей диаграмме здесь штриховыми квадратами показаны два индикатора хода часов на Земле. Один из них, оранжевый, отображает показания часов на Земле, которые вычислены по правилам специальной относительности, то есть без учета гравитационного замедления хода часов. Этот индикатор помечен буквой L (лоренцево замедление времени). Второй индикатор, голубого цвета, отображает время с учетом гравитационного замедления. Он помечен буквой g. Числовые значения часов выведены в отдельную табличку на диаграмме и помечены: At – показания часов на Земле с учетом только лоренцева замедления с точки зрения наблюдателя В; At' – показания часов на Земле с учетом как лоренцева замедления времени, так и гравитационного красного смещения с точки зрения наблюдателя В; Bt – показания часов наблюдателя В; Ax – расстояние между наблюдателями с точки зрения наблюдателя В. Все эти числовые значения показаний часов вычислены по правилам, соответственно, специальной (лоренцево замедление) и общей относительности (гравитационное замедление). 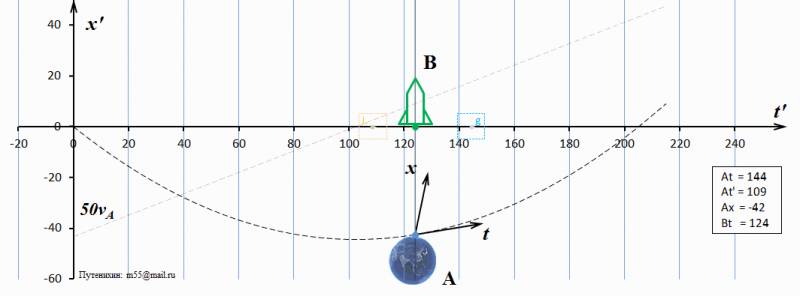Рис.2 Диаграмма Минковского – релятивистское решение «парадокса близнецов». Картина с точки зрения земного близнеца В. Как видим, отказ от учета гравитационного замедления времени приводит к фактическому парадоксу близнецов, что видно по индикатору лоренцева замедления времени. Он показывает, что в этом случае моложе должен оказаться улетавший близнец. Напротив, учет гравитационного замедления времени показывает, что часы на Земле с точки зрения космического корабля имеют более высокий темп, идут ускоренно по отношению к часам корабля. Собственно говоря, в этом и заключается решение парадокса близнецов. Правда, следует отметить неожиданную и довольно неприятную ситуацию. Конечно, согласно уравнениям общей относительности часы на Земле действительно идут более быстрым темпом и опережают часы на корабле. Но! Скрупулёзные расчёты этого опережения не дали абсолютно полного совпадения. С точки зрения Земли, часы на ней показали при встрече близнецов 240 месяцев. С точки зрения корабля, часы на Земле показали при встрече близнецов только 231 месяц. Расхождение почти 5%, но для аналитических выкладок в данном случае это чрезмерно. Точность вычислений – до трёх знаков после запятой. Разбиение отрезков при графическом интегрировании – от 240 до 50 000. Во всех случаях получался один и тот же результат – 231 месяц. Варьирование ускорения (вразрез с вычисленными) давало весьма незначительный эффект. Ни в одном случае не удалось получить 240 месяцев. Можно было бы предположить, что ускорение при развороте с точки зрения корабля было не постоянным. Но это крайне слабый довод. Ни завышение среднего ускорения, ни его занижение в расчетных формулах не давало необходимого результата. Вопрос об источнике погрешности, таким образом, остаётся открытым, но ответ на него лежит, несомненно, в плоскости рассмотренной модели, в неочевидных неточностях в допущениях. Рассмотрим подробнее вычисления, проделанные при формировании этих диаграмм. Движение земного близнеца с точки зрения космического корабля описывается такими же уравнениями, как (2), (3) и (4). Однако значения некоторых параметров движения, очевидно, будут другими. Действительно, время в пути космического корабля, как мы определили выше, составляет 205 месяцев. Следовательно, величина ускорения при движении Земли с точки зрения космонавта будет иной: (7) Кроме того, с ускорением движется всё-таки не Земля, а корабль, поэтому мы обязаны принять во внимание гравитационные релятивистские эффекты. Воспользуемся приведённым выше уравнением (1). Согласно принципу эквивалентности общей теории относительности, действие сил инерции при ускоренном движении тел эквивалентно действию гравитационного поля, создаваемого массивным телом. В этом случае, движущееся ускоренно тело может рассматриваться как покоящееся. Напротив, Земля с его точки зрения находится в свободном падении в эквивалентном гравитационном поле корабля. Это свободное падение Земли описывается уравнением (1): (1) В рассматриваемом варианте мы приняли, что скорость света равна единице, а величина ускорения - постоянная: Это ускорение вычисляем по формуле (7), а «высоту», с которой «падает» Земля в эквивалентном гравитационном поле корабля, находим по формуле (4). Подставляем их в уравнение (1) и производим тривиальные преобразования: Здесь t_B=205 – время в пути по часам корабля. Раскрываем скобки и группируем однотипные члены: Теперь можно подставить конкретные числовые значения: Уравнение имеет довольно странный, непривычный вид. Это связано с тем, что оно записано в ворде с помощью редактора формул и использования для простоты «скопировать» - «вставить». После упрощения получаем: Видим повторяющееся отношение, поэтому делаем очевидную упрощающую подстановку: Это уравнение и было использовано для вычисления гравитационного красного смещения при замедлении темпа хода часов Земли с точки зрения космического корабля. Как сказано, это уравнение позволяет производить своеобразное «табличное» интегрирования. Дробность интервала выбиралась 205, 300, 500 и 51252. Во всех случаях величина интеграла имела одно и то же значение – 230,73 месяца. Принцип эквивалентности можно продемонстрировать на такой условной, но в высшей степени наглядной диаграмме Минковского: Рис.3 Диаграмма Минковского – наглядная демонстрация принципа эквивалентности общей теории относительности на примере решения «парадокса близнецов». Картина с точки зрения близнеца В на космическом корабле. На диаграмме система отчета космического корабля изображена зелёной лужайкой или футбольным полем. На поле даже видна белая разметка. Нет никаких принципиальных препятствий считать, что космический корабль достаточно большой и на нём есть такое полноразмерное футбольное поле. На этом поле кто-то из игроков подбросил высоко вверх мяч. Обычный резиновый детский мяч, с двухцветной полоской по экватору. Задача, как видим, очень напоминает задачу из классической физики с подбрасыванием вертикально вверх камня. Ну, или можно с не меньшими основаниями считать, что мяч брошен под углом к горизонту. Или это был выстрел из пушки. Всё это эквивалентные картины. Но наша диаграмма ещё более условна. Мяч на самом деле, вовсе и не мяч. На самом деле это планета. Земля. И эта планета, как мяч, находится в свободном падении в «гравитационном» поле корабля. И здесь мы можем использовать всю мощь общей теории относительности. Поскольку «мяч» - Земля находится на некоторой высоте в «гравитационном» поле корабля, то часы на ней идут быстрее, чем на лужайке. Общая теория относительности предлагает конкретные уравнения для вычисления этого «ускорения» хода часов (1). На числовой шкале вдоль горизонтальной разметки «футбольного поля» движутся три метки: квадрат с буквой L внутри, полупрозрачный круг и квадрат с буквой g. Буква L обозначает, как уже было сказано, традиционный, лоренцев «парадокс близнецов». Это темп хода часов, без учета гравитации. Это «неправильные» часы. Полупрозрачный кружок – это, как нетрудно догадаться, тень от «мяча» - Земли, показывающая равномерный ход часов на корабле – время «настоящего».. В момент «падения» Земли-мяча на лужайку, она сливается с собственной тенью. И, наконец, «правильные» гравитационные часы g, которые движутся по оси времени t, отмечая на ней время, которое соответствует расчетам по правилам общей теории относительности. Как я выше признал, показания этих часов по неизвестной причине всё-таки несколько отклоняются от ожидаемых показаний, необходимых для точного решения парадокса. Научный метод Научный метод – это метод проб и ошибок. Многие, кто когда-то был студентом или сейчас студент, наверняка слышали, да и, вероятно, использовали основные практические приложения этого метода: метод «научного тыка» и подгонки решения под известный ответ. Эти шутливые названия методов имеют и более солидные варианты: «экспериментальная наука» и создание (подгонка) теории, способной объяснить новые явления (известный ответ), соответственно. Можно попытаться предположить, по какой причине результат не совпал с ожидаемым. При вычислениях мы использовали уравнение общей теории относительности: Может быть, подставляемые в него значения выбраны неверно? Действительно, в этом уравнении есть величины, значения которых не могут быть выбраны произвольно. Например, u - скорость Земли с точки зрения корабля. Это относительная скорость и её значение точно определено для каждой точки пространства. Ускорение g также задано неизменным и нет никаких убедительных доводов в пользу того, что с точки зрения корабля оно меняется в процессе движения. Действительно, с точки зрения Земли в «падающем лифте» - корабле можно наблюдать пружинные весы, которые под действием постоянного ускорения уравновешивают некую массу, отклонившись (провиснув) на вполне определенную, фиксированную величину. Следовательно, с точки зрения корабля, эти показания «весов» не могут быть иными: они всегда будут установлены на одно и то же деление их шкалы. Но в нём есть и величина, значение которой может трактоваться, в общем-то, не вполне однозначно. Это величина x – расстояние между Землёй и кораблём. Она может быть переменной величиной в уравнении, то есть зависимой от точки зрения. Мы приняли изначально, что это удалённость Земли от корабля с точки зрения корабля. И в результате получили результат, который нас не вполне устраивает. А что если попробовать просто подогнать решение под требуемый ответ? Предположим, что в уравнении должно присутствовать расстояние между кораблем и Землёй по измерениям с Земли. Тогда уравнение примет вид: (8) Беглый взгляд позволяет предположить, что в процессе математических преобразований уравнения корень под корнем наверняка приведёт к длинному и «заковыристому» выражению. Поэтому мы не будем делать такого противоестественного «упрощения», вспомнив, что у нас в распоряжении есть метод табличного интегрирования и инструмент для него – компьютер. Запишем интеграл выражения (8) в виде суммы: и произведём его вычисление как суммы конечного числа отрезков Δt вместо dt на заданном интервале по известным параметрам: где: dτ, dt – дифференциалы времени, прошедшего по часам, соответственно, на «падающем» (Земля) и на гравитирующем теле (космическом корабле); Δt – интервал времени, прошедшего по часам «гравитирующего» (корабль) тела; x_B – расстояние между кораблём из Землёй с точки зрения корабля; t_B = 205 – «время в пути» Земли с точки зрения корабля (в месяцах); – «ускорение» свободного падения в гравитационном поле корабля (единицах, соответствующих единичной скорости света); – начальная скорость движения Земли по отношению к кораблю (в долях скорости света). Используя полученные уравнения, произведём все вычисления и внесём их в Таблицу 1. Таблица 1 Колонка 5 таблицы – это искомые приращения времени по часам Земли с точки зрения наблюдателя на корабле. Как мы ни старались, а сумма всех приращений так и не достигла требуемого значения – 240 месяцев. Мы сделали весьма произвольное допущение, что при вычислении замедления времени по формулам общей теории относительности с точки зрения ускоренно движущейся системы отсчета, расстояние до удаленного объекта берётся с точки зрения этого объекта. Но даже в этом случае результат оказался не точным. Таблица служит лишь демонстрацией, поэтому приведена с сокращениями: в ней удалены два средних блока, чтоб уменьшить занимаемый ею на экране размер. Колонка 1 таблицы – это время по часам корабля. За 205 месяцев наблюдатель на корабле ожидает, что по часам Земли пройдёт 240 месяцев. Колонка 2 – это скорость «падения» Земли в эквивалентном гравитационном поле корабля. В колонках 3 и 4 приведены расстояния между кораблём и Землёй с точки зрения корабля и Земли, соответственно. Сумма приращений интервалов времени по часам Земли с точки зрения корабля дала в итоге 237 месяцев. Для проверки точности были проведены более дискретные вычисления, в которых каждый интервал времени разбивался ещё на 100 частей. Общая длина таблицы при этом составила свыше 20 тысяч строк. При суммировании общее время по часам Земли составило 237,2 месяца, что свидетельствует о достаточной точности при дискретном суммировании интервалов. Кроме того, при более мелких интервалах сумма не возрастает, а уменьшается, поэтому нет необходимости проверять её для ещё более мелких интервалов. Итак, мы видим, что отклонение в показаниях часов Земли с точки зрения двух наблюдателей уменьшилось до (240-237)/240=0,0125, то есть, чуть больше одного процента. Следует признать это не удовлетворительным итогом. В заключение кто-нибудь вполне обоснованно может сказать: это совсем даже не подгонка под известный ответ, это больше похоже на притягивание ответа «за уши». И с этим весьма трудно будет не согласиться. Поэтому считать приведённые выкладки как безусловное подтверждение решения парадокса близнецов средствами общей теории относительности следует с определённой осторожностью. 29.03.2014 Литература 1. Мардер Л., «Парадокс часов», Пер. с англ. А.А.Бейлинсона, с предисловием Н.В.Мицкевича, Изд. «МИР», Москва, 1974. 2. Мёллер К., Теория относительности, Изд. 2-е. Пер. с англ. Под ред. проф. Д. Иваненко. М.: Атомиздат, 1975, 400 с., URL: http://bib.convdocs.org/v25205/?download=1 (дата обращения 05.12.2015) 3. Розман Г.А. Теория относительности, ч.2 - Псков: ПГПУ, 2005. - 256 с., URL: http://rozman2.narod.ru/oto.html (дата обращения 05.12.2015) http://rozman2.narod.ru/otopdf/oto04.pdf (дата обращения 05.12.2015) 4. Скобельцын Д.В., «Парадокс близнецов в теории относительности», АН СССР, М.- «Наука», 1966 Адрес полного текста статьи в интернете URL: http://samlib.ru/editors/p/putenihin_p_w/ddm4-oto.shtml Иллюстрации и уравнения к статье (зеркала) http://samlib.ru/editors/p/putenihin_p_w/ https://cloud.mail.ru/public/8WpP/qeaUMAiGz https://yadi.sk/d/EZg36rrKmJDwk http://vixra.org/author/putenikhin_p_v
Категория: Разное \| Добавил: m55 \| Теги: (близнецов), Путенихин, парадокса, нет!, П.В., больше, итак
Просмотров: 3274 \| Загрузок: 45