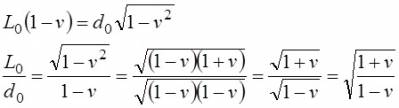Путенихин П.В. Мнимые парадоксы СТО. Парадокс арбалета
| [ Скачать с сервера (3.26 Mb) ] | 09.02.2016, 19:27 |
Путенихин П.В. m55@mail.ru Аннотация Рассмотрен парадокс арбалетной стрелы. Металлическая стрела пробивает обкладки конденсатора. В ИСО стрелы конденсатор разряжается, в ИСО конденсатора – стрела слишком коротка. Возникает, как кажется автору парадокс СТО. Показано, что формулировка парадокса ошибочна. Парадокса нет. Подбирая материал по парадоксу транспортера, я нашел в интернете лишь две ссылки на него. В первой из них даётся развернутое описание и решение парадокса, а во второй лишь его упоминание: «Уже в то время появились многочисленные парадоксы («парадокс колеса», «парадокс транспортёра», «парадокс часов» и т.п.), не имеющие вполне удовлетворительного объяснения» [1]. Однако, само сообщение являлось описанием ещё одного, видимо нового – от сентября 2005 года, ранее не публиковавшегося «парадокса» - «парадокса арбалетной стрелы или парадокса железного крокодила». Текст был выложен на интернет-форуме, автор представился как Диоген Московский. При цитировании описания [1] для лучшего восприятия текста я заменю словесные обозначения типа «эл нулевое» на соответствующие математические обозначения и пропущу фрагменты, не имеющие непосредственного отношения к «парадоксу». «Пусть имеется источник электрического тока (заряженный конденсатор), подключенный через амперметр к двум параллельным медным пластинам, расстояние между которыми равно d0. Так как цепь разомкнута, то эл. ток отсутствует, конденсатор не разряжается, и амперметр показывает ноль. Чтобы цепь замкнулась, нужно поместить между пластинами токопроводящую перемычку. В качестве такой перемычки используем железную арбалетную стрелу …, длина которой L0 больше расстояния между пластинами d0. Пусть стрела посылается из арбалета со скоростью v, пробивает сначала первую пластину, затем вторую. В момент, когда остриё стрелы касается второй пластины, а с первой пластиной контакт сохраняется, в цепи происходит кратковременный разряд конденсатора (стрелка амперметра дёргается), между стрелой и пластинами проскакивают искры. Но это в том случае, когда скорость стрелы невелика, и её длина больше d0. Если же стрела движется с околосветовой скоростью, то в соответствии с «преобразованиями Лоренца» её длина сокращается и становится равной 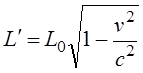 где v - скорость стрелы относительно пластин, c - скорость света в вакууме. И если v превышает критическую скорость (при которой L'= d0), то длина стрелы становится меньше расстояния между пластинами, и цепь остаётся разомкнутой, конденсатор не разряжается, искра не проскакивает, стрелка амперметра не дёргается. 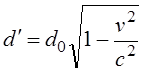 Теперь переходим в «систему отсчёта» связанную с наблюдателем, движущимся со скоростью v вместе со стрелой. Относительно этого наблюдателя стрела покоится, и её длина равна L0. Расстояние между медными пластинами, движущимися относительно стрелы со скоростью v, относительно этого наблюдателя равно т.е. в системе отсчёта стрелы расстояние между пластинами ВСЕГДА МЕНЬШЕ ДЛИНЫ СТРЕЛЫ И, СТАЛО БЫТЬ, СТРЕЛА ВСЕГДА, ПРИ ЛЮБОЙ СКОРОСТИ ДВИЖЕНИЯ СОЗДАЁТ КРАТКОВРЕМЕННЫЙ КОНТАКТ, приводящий к разряду конденсатора и отклонению стрелки амперметра (скорость эл. тока, как известно, равна скорости света, которая инвариантна: «Ток — направленное движение заряженных электрических частиц. Величина тока измеряется так называемой силой тока которая измеряется в амперах. Скорость движения частиц зависит от материала проводника, массы и заряда частицы, окружающей температуры, приложенной разности потенциалов и составляет величину, намного меньшую скорости света. Несмотря на это, скорость распространения собственно электрического тока равна скорости света в данной среде, т. е. скорости распространения фронта электромагнитной волны...» Продолжение находим в следующем сообщении на форуме. «у нас же, в данном эксперименте, используется железная перемычка (арбалетная стрела), скорость распространения электромагнитной волны в которой равна скорости света в вакууме… Таким образом, мы неизбежно приходим к признанию того факта, что ПРИ ПОСЛЕДОВАТЕЛЬНОМ ПРИМЕНЕНИИ «ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ» ИМЕЕТ МЕСТО НАРУШЕНИЕ ПРИЧИННОСТИ - когда в одной «системе отсчёта» (связанной с летящей стрелой или с бегущим крокодилом) событие (замыкание контактов) ПРОИСХОДИТ ВСЕГДА, а в другой «системе отсчёта» (связанной с контактами-пластинами) - не происходит (L' короче, чем d0, и одновременного контакта перемычки с пластинами, что явл. НЕОБХОДИМЫМ УСЛОВИЕМ ДЛЯ ЗАМЫКАНИЯ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ, нет) … Полагаю, теперь можно наконец поставить точку в споре с релятивизмом! На «парадокс арбалетной стрелы» релятивистам возразить нечего!» Вывод ожидаемый. Известно, что основной целью выявления парадоксов в специальной теории относительности является стремление показать её внутренние противоречия, что означало бы несостоятельность теории. Но все парадоксы, в конечном счете, оказываются мнимыми, сформулированными на основе ошибочных высказываний, предсказаний, которые не являются высказываниями, предсказаниями специальной теории относительности и противоречат ей. Это касается и описанного «парадокса арбалетной стрелы». Рассмотрим его более детально и найдём ошибку в формулировании этого мнимого парадокса. В качестве иллюстраций используем анимации. Мы откажемся от амперметра и будем пробивать стрелой сам конденсатор, состоящий из двух пластин. По завершению опыта мы можем проверить, сохранился ли заряд на его пластинах любым доступным физическим методом. Если стрела замкнёт пластины, то разницы потенциалов (зарядов) на них не будет. Автор рассматривает вариант, когда стрела длиннее расстояния между пластинами. Но для начала будем считать, что они равны: длина стрелы L0 в точности равна расстоянию между пластинами d0. Это гарантированно делает при движении её длину меньше расстояния между пластинами. Скорость движения выберем определённо субсветовой, «околосветовой», причём для удобства вычислений и построений, пусть она будет такой v=0,968246с, что коэффициент лоренцева сокращения будет в точности равен 0,25. То есть, при движении с этой скоростью стрела сократится ровно в 4 раза. Здесь и далее по возможности будем использовать систему единиц, в которой скорость света с=1. Уравнения Лоренца выглядят компактнее, если вместо абсолютной скорости ИСО использовать её скорость в долях от скорости света. Действительно: 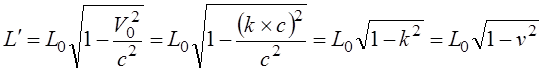 где k - доля скорости ИСО от скорости света и которую удобно обозначать символом скорости v. Для заданной скорости получаем: 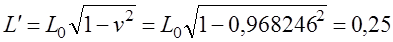 Анимация пробоя пластин с точки зрения ИСО конденсатора приведена на рисунке: Рис.1 Пластины конденсатора пробиваются арбалетной стрелой. Вследствие лоренцева сокращения стрела в ИСО конденсатора не может одновременно коснуться двух пластин, замкнуть и разрядить конденсатор. Анимация: Как мы видим, на анимации при равенстве в состоянии покоя длины стрелы и расстояния между пластинами конденсатора разряда не будет, поэтому на анимации мы заканчиваем полёт стрелы до того, как она коснётся второй пластины, в этом нет смысла, всё и так очевидно. Напротив, если перейти в ИСО стрелы, то укороченным окажется расстояние между пластинами. Теперь уже стрела вполне может коснуться обеих пластин одновременно и, как ожидается, разрядить конденсатор: Рис.2 Пластины конденсатора пробиваются арбалетной стрелой. Вследствие лоренцева сокращения, в ИСО стрелы расстояние между пластинами меньше длины стрелы. Однако, разряда конденсатора не будет. Анимация: Но это лишь кажущийся результат. Разряда пластин не будет! В собственной системе покоя стрела не сокращается и имеет исходную длину. Расстояние между движущимися пластинами при выбранной скорости, напротив, сократится в 4 раза и будет меньше длины стрелы. Следовательно, какое-то время стрела будет касаться одновременно обеих пластин, что, казалось бы, должно вызвать разряд конденсатора. Но это неверное предположение. Фронт электростатического поля движется в металле стрелы со скоростью света, но сами пластины также движутся со скоростью, близкой к скорости света. Фронт волны, согласно второму постулату (принципу) специальной теории относительности, будет двигаться относительно стрелы строго рядом с таким же фронтом светового луча, который мог быть испущен от острия стрелы в момент касания. Действительно, второй постулат (принцип) специальной теории относительности утверждает, что скорость световой волны не зависит от того, испускается она покоящимся или движущимся телом: «Каждый луч света движется в «покоящейся» системе координат с определенной скоростью V, независимо от того, испускается ли этот луч света покоящимся или движущимся телом» (Эйнштейн, «К электродинамике движущихся тел», 1905 г.) Это означает, что фронт поля будет всегда идти «ноздря в ноздрю» с лучом света, испущенным от кончика стрелы в тот момент, когда она коснётся второй пластины. При этом первая пластина (левая) удаляется от кончика стрелы почти со скоростью света - 0,968с, но всё-таки меньшей, чем скорость света. Хотя электростатическое поле в металле стрелы и распространяется со световой скоростью, но вторая пластина непрерывно «убегает» от его фронта и световой волне не хватит времени, чтобы её догнать, что и показано на анимации. Анимация построена на основе расчетов по уравнениям СТО и на ней хорошо видно, что в момент выхода стрелы из второй (левой) пластины, фронт волны электростатического поля так её и не достиг. Движения электрических зарядов нет, тока нет, разряда конденсатора нет. Мы здесь обязаны определённо признать: специальная теория относительности сделала два тождественных предсказания в отношении одного и того же процесса: пробития конденсатора стрелой. Парадокса нет. Приведём эти уравнения, на основе которых построена анимация. В системе отсчета конденсатора, в его ИСО стрела будет иметь длину: 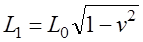 Изначально для удобства построений мы выбрали коэффициент лоренцева сжатия, равный четырем. То есть: 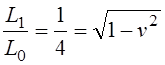 Такое сжатие будет происходить при скорости: 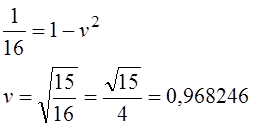 Для простоты примем, что длина стрелы L0=1. Очевидно, что время на преодоление этого интервала лучом света или фронтом электростатического поля равно: 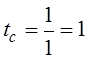 Нетрудно убедиться, что каждая пластина конденсатора пройдёт за время парного контакт только 0,75 длины стрелы. На это у них при движении с выбранной скоростью уйдет время: 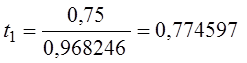 Это время, в течение которого сохраняется контакт между пластинами, одновременный, парный контакт их со стрелой. С другой стороны, за это время парного контакта фронт электростатического поля со скоростью света пройдёт путь в долях длины стрелы: 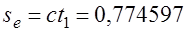 Таким образом, левая пластина за это время дойдёт до конца стрелы, правая пластина – до отметки 0,75 от её длины, а фронт поля – до отметки около 0,77 от её длины. Эти значения заложены в алгоритм построения анимации. Как видим, фронт поля не успел догнать вторую (левую) пластину до того, как стрела вышла из неё. Отметим, что решение не зависит от абсолютной длины стрелы и расстояния между пластинами. Достаточно того, что в состоянии покоя они равны. Действительно, при движении расстояние между пластинами конденсатора сократится до величины: 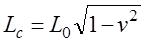 При движении со скоростью v время совместного контакта составит: 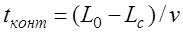 Или: 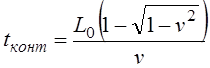 За это время фронт пройдёт путь в долях от длины стрелы: 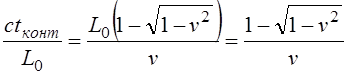 Правая пластина, очевидно: 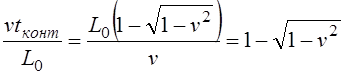 Для рассмотренного выше примера получаем вычисленное выше значение для пути, пройденного фронтом поля: 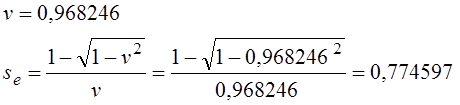 Полученные выражения позволяют сделать вывод, что при равенстве этих длин, конденсатор не будет разряжен ни при какой скорости. Чтобы фронт поля за время парного контакта прошёл всю длину стрелы, se должно быть равно единице. Это достигается лишь при движении конденсатора со скоростью света, что невозможно. Длинная стрела В оригинальной версии парадокса принято, что длина стрелы несколько больше расстояния между пластинами конденсатора. В принятых авторских обозначениях в состоянии покоя длина стрелы L0, а расстояние между обкладками d0. Используя систему единиц с единичной скоростью света c=1, получаем, что в системе отсчета стрелы расстояние между обкладками при движении со скоростью v сжимается до: 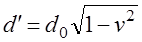 Время на прохождение стрелы сквозь конденсатор от момента входа стрелы во вторую обкладку и до выхода конца стрелы из первой обкладки составляет: 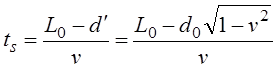 Это действительно так, поскольку в процессе взаимодействия стрелы и конденсатора левая пластина происходит интервал, расстояние на d` меньшее, чем длина L0 стрелы. До него и после него нет контакта между стрелой и конденсатором, приводящего к его разряду. С другой стороны, собственно разряд конденсатора не может начаться раньше, чем стрела коснётся правой (второй) обкладки. Следовательно, именно столько времени – ts есть и у правой обкладки, чтобы передать сигнал левой обкладке в виде фронта электростатического поля, движущегося со скоростью света. Поэтому очевидно, что в момент касания стрелой правой обкладки разряд конденсатора не может начаться: электростатическое поле даже со скоростью света ещё не достигло второй обкладки. Посмотрим, какой точки достигнет это поле в момент выхода стрелы из левой обкладки. Мы вычислили, что время на передачу этого сигнала равно ts, значит, сигнал поля за это время пройдёт cо скоростью света путь сts или, с учетом принятой системы единиц, в которой с=1, ts. Сравним путь, пройденный фронтом поля и длину стрелы через их отношение: 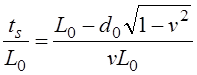 Например, для рассмотренного выше случая равенства длин и скорости v=0,968246с получаем: 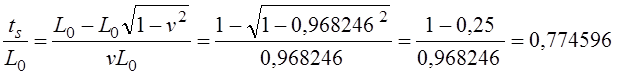 Как вычислено выше, за время парного контакта путь, пройденный фронтом поля, составляет в долях длины стрелы ts=0,77. Как видим, фронт электростатического поля так и не достиг конца стрелы, за время, пока она была совмещена с левой обкладкой конденсатора, время парного контакта. Сигнал поля прошёл лишь часть расстояния между обкладками конденсатора d0/(ts-(L0-d0)) = 0,25/(0,77-0,75) = 0,25/0,02 ~ 12,5 – примерно тринадцатую часть этого расстояния, что показано и на анимации. Теперь рассмотрим вариант, когда сигнал поля всё-таки достигнет конца стрелы до того, когда стрела выйдет из второй обкладки, то есть: 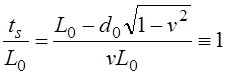 Очевидно, что это тот момент, когда разряд конденсатора, начавшись, так и не завершится, поскольку это отношение соответствует и моменту его завершения, то есть, это предельное значение длин и скорости. Из выражения находим: 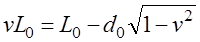 Преобразуем выражение таким образом, чтобы узнать предельное, крайнее значение отношения длины стрелы и расстояния между обкладками, при котором разряд возможен: Для рассмотренного выше равенства длин как следствие можно получить результат: 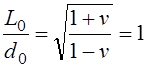 Как видим, не существует такой скорости v, при которой это равенство соблюдается: при равенстве длины стрелы и расстояния между обкладками конденсатора световой сигнал электрического поля не успевает достичь второй обкладки. Как выяснено выше, конденсатор не будет разряжен также и с точки зрения системы отсчета стрелы. Из полученного выражения следует, что разрядка конденсатора может начаться лишь при отношении длин, соответствующем каждой конкретной скорости. Для рассмотренной нами скорости в 0,968246с это отношение равно: 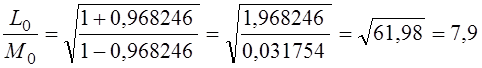 Это значит, что разряд конденсатора может начаться, только если длина стрелы больше ширины конденсатора примерно в 8 раз и более. Поэтому заявление автора «парадокса» о том, что стрела длиннее расстояния между пластинами, по крайней мере, неточное. Это «длиннее» не может превышать величины, соответствующей полученному выражению. Если длина больше, то конденсатор будет разряжен с любой точки зрения. Покажем это наглядно на анимации, на которой длина стрелы в 8 раз больше расстояния между обкладками в состоянии покоя. Следующий рисунок соответствует системе отсчета стрелы: Рис.3 Пластины конденсатора пробиваются арбалетной стрелой. Несмотря на лоренцево сокращение, стрела в ИСО конденсатора при некоторой длине может одновременно коснуться двух пластин и разрядить конденсатор. Анимация: Если при выбранной скорости движения расстояние между пластинами конденсатора в состоянии покоя будет в 8 раз меньше длины стрелы, то разряд конденсатора произойдёт. На рисунке тонкой вертикальной стрелкой показано положение второй (правой) пластины, если расстояние между ними в состоянии покоя уменьшить в 8 раз. На анимации паузами зафиксированы моменты, когда стрела коснется второй пластины и когда она выйдет из первой (левой) пластины. Хорошо видно, что в момент касания левая пластина находится ровно посередине стрелы. Следовательно, фронт электростатического поля, начав движение в этот момент, определённо достигнет второй пластины раньше, чем конец стрелы выйдет из первой. Разряд конденсатора будет осуществлен. Правда, следует уточнить, для того чтобы весь заряд перетёк с пластины на пластину, стрела должна быть чуть длиннее, чем предельное значение. Кратность длин 8 соответствует возможности начала процесса разрядки конденсатора. Предельное значение равно 7,9 и отношение 8, возможно, обеспечит завершение разряда. Казалось бы, очевидный разряд с точки зрения ИСО стрелы, как оказалось, и показано на анимации, не всегда осуществим. Возможным он становится только в случае более длинной стрелы, чем ширина конденсатора. На рисунке – анимации показано, что при отношении длин, равном 8, фронт поля успевает достичь второй пластины до того, как стрела выйдет из неё: Рис.4 Пластины конденсатора пробиваются арбалетной стрелой. Несмотря на то, что вследствие лоренцева сокращения ширина конденсатора стрела в ИСО стрелы многократно короче стрелы, на разряд конденсатора отводится лишь короткий интервал. На анимации выше было видно, что поле не успевает достичь второй пластины до выхода из неё стрелы. На данном рисунке тонкой вертикальной стрелкой показано новое положение левой пластины по отношению к правой в ИСО стрелы, когда ширина конденсатора в состоянии покоя меньше длины стрелы в 8 раз. При таком соотношении длин, как видно на анимации, фронт поля успевает достичь второй, «тонкой» пластины до того, как стрела выйдет из неё. Итак, мы увидели, что парадоксальные предсказания об арбалетной стреле, сделанные цитируемым автором, не соответствуют предсказаниям специальной теории относительности. Автор, как показано, исходил из ошибочных представлений об этой теории. Кроме того, верно ссылаясь на законы электротехники, в описании своего парадокса он их использовал с ошибками. По его выкладкам получилось, что электростатическое поле в металлах распространяется со сверхсветовой скоростью или даже мгновенно. Формализм СТО автор использовал некорректно, не увидев, что даже при верной её трактовке при указанном им соотношении длины стрелы L0 и расстояния между пластинами d0 существуют два варианта: конденсатор может быть как разряжен стрелой, так и не разряжен. Указанное автором значение «стрела длиннее расстояния между пластинами» допускает оба решения. Парадоксом в теории принято считать два правильных утверждения, противоречащих друг другу. Мы увидели, что при последовательном и корректном применении положений специальной теории относительности в рассмотренной задаче оба утверждения теории верны и не противоречат друг другу. Это означает, что в данном случае парадокса нет, и «парадокс арбалетной стрелы», таким образом, является мнимым, не существующим парадоксом. Это просто рядовая задача теории относительности, при формулировке которой были допущены ошибки. Теории относительности приписаны утверждения, которые сделаны, якобы, от её имени, а на самом деле от имени автора, ошибочно её трактующего. Теория относительности не делает парадоксальных утверждений, просто не надо приписывать ей того, чего она не утверждает [2]. В заключение замечу, что парадокс арбалетной стрелы довольно схож с парадоксом шеста и сарая или с парадоксом тележки и ямы. И там и там делаются попытки «приложить» друг к другу релятивистки сокращающиеся объекты, получая выводы, противоречащие друг другу. Литература 1.Диоген Московский, «Парадокс арбалетной стрелы или парадокс железного крокодила», 2005, URL: http://physics-animations.com/efrboard/messages/179.html http://physics-animations.com/efrboard/messages/181.html 2.Путенихин П.В., Три ошибки анти-СТО, 2011, URL: http://samlib.ru/p/putenihin_p_w/antisto.shtml Адрес статьи в интернете URL: http://samlib.ru/p/putenihin_p_w/paradox-arbalet.shtml Иллюстрации и уравнения к статье (зеркала) http://samlib.ru/editors/p/putenihin_p_w/ https://cloud.mail.ru/public/8WpP/qeaUMAiGz https://cloud.mail.ru/public/Hq7e/jZ9YZGJW9 https://yadi.sk/d/EZg36rrKmJDwk https://drive.google.com/folderview?id=0B0uM56-EnG4ZaUFJb0YzY3YtcVU&usp=drive_web http://fileload.info/users/putenikhin/ 07.10.2015 | |
| Категория: Разное | | | |
| Просмотров: 3415 | Загрузок: 86 | |
| Всего комментариев: 0 | |