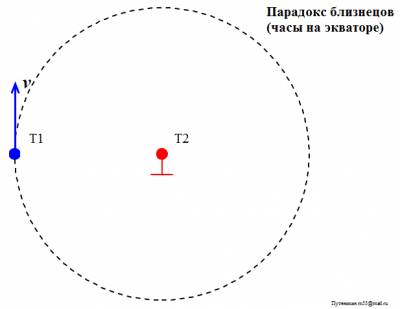
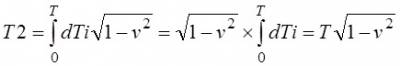Путенихин П.В., Мнимые парадоксы СТО. Парадокс близнецов
| 09.02.2016, 18:53 | |
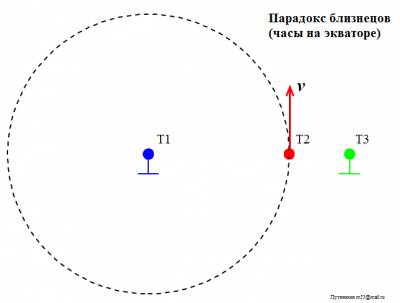
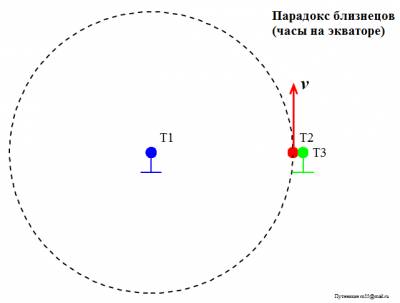
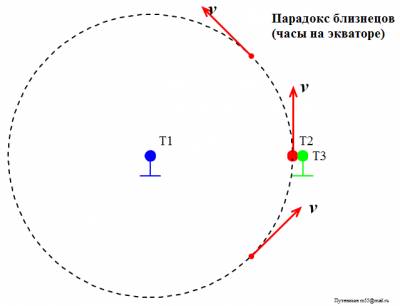
Путенихин П.В. m55@mail.ru Аннотация Парадокс близнецов, он же парадокс Ланжевена, он же парадокс часов – это первый и наиболее известный парадокс СТО, основанный на тезисе, сформулированном Эйнштейном в основополагающей работе «К электродинамике движущихся тел». Статус «парадокса» появился позднее. В предлагаемой работе показано, что задача о близнецах не является парадоксом, это рядовая задача специальной теории относительности, имеющая в ней однозначное, непротиворечивое решение. В литературе и в интернете до сих пор идут многочисленные дискуссии по этому парадоксу. Предложено и продолжает предлагаться множество его решений (объяснений), из которых делаются выводы как о непогрешимости СТО, так и её ложности. Впервые тезис, послуживший основой для формулировки парадокса, был изложен Эйнштейном в его основополагающей работе по специальной (частной) теории относительности «К электродинамике движущихся тел» в 1905 году: «Если в точке А находятся двое синхронно идущих часов и мы перемещаем одни из них по замкнутой кривой с постоянной скоростью до тех пор, пока они не вернутся в А (...), то эти часы по прибытии в А будут отставать по сравнению с часами, остававшимися неподвижными...». В дальнейшем этот тезис получил собственные имена «парадокс часов», «парадокс Ланжевена» и «парадокс близнецов». Последнее название прижилось, и в настоящее время чаще встречается формулировка не с часами, а с близнецами и космическими полётами: если один из близнецов улетает на космическом корабле к звёздам, то по возвращению он оказывается моложе своего остававшегося на Земле брата. Гораздо реже обсуждается другой, сформулированный Эйнштейном в этой же работе и следующий сразу же за первым, тезис об отставании часов на экваторе от часов, находящихся на полюсе Земли. Смыслы обоих тезисов совпадают: «… часы с балансиром, находящиеся на земном экваторе, должны идти несколько медленнее, чем точно такие же часы, помещённые на полюсе, но в остальном поставленные в одинаковые условия». На первый взгляд это утверждение может показаться странным, ведь расстояние между часами неизменно и нет относительной скорости между ними. Но на самом деле на изменение темпа хода часов влияет мгновенная скорость, которая, хотя и меняет непрерывно своё направление (тангенциальная скорость экватора), но все в сумме они дают ожидаемое отставание часов. Парадокс, кажущееся противоречие в предсказаниях теории относительности возникает, если движущимся близнецом считать того, который оставался на Земле. В этом случае теперь уже улетавший в космос близнец должен ожидать, что остававшийся на Земле брат окажется моложе него. Так же и с часами: с точки зрения часов на экваторе движущимися следует считать часы на полюсе. Таким образом, и возникает противоречие: так кто же из близнецов окажется моложе? Какие из часов покажут время с отставанием? Чаще всего парадоксу обычно даётся простое объяснение: две рассматриваемые системы отсчета на самом деле не являются равноправными. Близнец, который улетал в космос, в своём полёте не всегда находился в инерциальной системе отсчета, в эти моменты он не может использовать уравнения Лоренца. Так же и с часами. Отсюда следует сделать вывод: в СТО не может быть корректно сформулирован «парадокс часов», специальная теория не делает двух взаимоисключающих предсказаний. Полное решение задача получила после создания общей теории относительности, которая решила задачу точно и показала, что, действительно, в описанных случаях отстают движущиеся часы: часы улетавшего близнеца и часы на экваторе [2]. «Парадокс близнецов» и часов, таким образом, является рядовой задачей теории относительности. Задача об отставании часов на экваторе Мы опираемся на определение понятия «парадокс» в логике как противоречия, полученного в результате логически формально правильного рассуждения, приводящего к взаимно противоречащим заключениям (Энциплопедический словарь), или как два противоположных утверждения, для каждого из которых имеются убедительные аргументы (Логический словарь). С этой позиции, «парадокс близнецов, часов, Ланжевена» парадоксом не является, поскольку нет двух взаимоисключающих предсказаний теории. Сначала покажем, что тезис в работе Эйнштейна о часах на экваторе полностью совпадает с тезисом об отставании движущихся часов. На рисунке показаны условно (вид сверху) часы на полюсе Т1 и часы на экваторе Т2. Мы видим, что расстояние между часами неизменно, то есть, между ними, казалось бы, нет необходимой относительной скорости, которую можно подставить в уравнения Лоренца. Однако, добавим третьи часы Т3. Они находятся в ИСО полюса, как и часы Т1, и идут, следовательно, синхронно с ними. Но теперь мы видим, что часы Т2 явно имеют относительную скорость по отношению к часам Т3: сначала часы Т2 находятся на близком расстоянии от часов Т3, затем они удаляются и вновь приближаются. Следовательно, с точки зрения неподвижных часов Т3 движущиеся часы Т2 отстают: Рис.1 Движущиеся по окружности часы отстают от часов, находящихся в центре окружности. Это становится более очевидно, если добавить неподвижные часы вблизи от траектории движущихся. Следовательно, часы Т2 отстают также и от часов Т1. Переместим теперь часы Т3 настолько близко к траектории Т2, что в какой-то начальный момент времени они окажутся рядом. В этом случае мы получаем классический вариант парадокса близнецов. На следующем рисунке мы видим, что сначала часы Т2 и Т3 были в одной точке, затем часы на экваторе Т2 стали удаляться от часов Т3 и по замкнутой кривой через некоторое время вернулись в исходную точку: Рис.2. Движущиеся по окружности часы Т2 сначала находятся рядом с неподвижными часами Т3, затем удаляются и через некоторое время вновь сближаются с ними. Это полностью соответствует формулировке первого тезиса об отставании часов, послужившего основой «парадокса близнецов». Но часы Т1 и Т3 идут синхронно, следовательно, часы Т2 отстали также и от часов Т1. Таким образом, оба тезиса из работы Эйнштейна в равной степени могут служить основой для формулировки «парадокса близнецов». Величина отставания часов в этом случае определяется уравнением Лоренца, в которое мы должны подставить тангенциальную скорость движущихся часов. Действительно, в каждой точке траектории часы Т2 имеют скорости, равные по модулю, но разные по направлениям: Рис.3 Движущиеся часы имеют постоянно изменяющееся направление скорости. Как эти разные скорости внести в уравнение? Очень просто. Давайте, в каждую точку траектории часов Т2 поместим свои собственные неподвижные часы. Все эти новые часы идут синхронно с часами Т1 и Т3, поскольку все они находятся в одной и той же неподвижной ИСО. Часы Т2, проходя каждый раз мимо соответствующих часов, испытывает отставание, вызванное относительной скоростью именно мимо этих часов. За мгновенный интервал времени по этим часам, часы Т2 также отстанут на мгновенно малое время, которое можно вычислить по уравнению Лоренца. Здесь и далее мы будем использовать одни и те же обозначения для часов и их показаний: 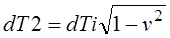 Здесь и далее мы будем использовать систему единиц, в которой скорость света c=1. Проинтегрируем это выражение по всем часам и найдём суммарное время отставания: Очевидно, что верхним пределом интегрирования являются показания часов Т3 в момент, когда часы Т2 и Т3 вновь встретятся. Как видим, показания часов Т2 < T3 = T1 = T. Лоренцев множитель мы выносим из-под знака интеграла, поскольку он является константой для всех часов. Введённое множество часов можно рассматривать как одни часы - «распределённые в пространстве часы». Это «пространство часов», в котором часы в каждой точке пространства идут синхронно и обязательно некоторые из них находятся рядом с движущимся объектом, с которым эти часы имеют строго определённое относительное (инерциальное) движение. Как видим, получено решение, полностью совпадающее с решением первого тезиса (с точностью до величин четвертого и высших порядков). По этой причине, дальнейшие рассуждения можно рассматривать как относящиеся ко всем видам формулировок «парадокса близнецов». Вариации на тему «парадокса близнецов» Парадокс часов, как отмечено выше, означает, что специальная теория относительности, вроде бы, делает два взаимно противоречащих друг другу предсказания. Действительно, как мы только - что вычислили, движущиеся по окружности часы отстают от часов, находящихся в центре окружности. Но и часы Т2, движущиеся по окружности, имеют все основания утверждать, что они находятся в центре окружности, вокруг которой движутся неподвижные часы Т1. Уравнение траектории движущихся часов Т2 с точки зрения неподвижных Т1: x2 + y2 = R2 где, x, y – координаты движущихся часов Т2 в системе отсчета неподвижных; R – радиус окружности, описываемой движущимися часами Т2. Очевидно, что с точки зрения движущихся часов Т2, расстояние между ними и неподвижными часами Т1 также равно R в любой момент времени. Но известно, что геометрическим местом точек, равно удалённых от заданной, является окружность. Следовательно, и в системе отсчета движущихся часов Т2, неподвижные часы Т1 движутся вокруг них по окружности: x12 + y12 = R2 где, x1, y1 – координаты неподвижных часов Т1 в системе отсчета движущихся; R – радиус окружности, описываемой неподвижными часами Т1. Рис.4 С точки зрения движущихся часов Т2 вокруг них по окружности движутся неподвижные часы Т1. А это, в свою очередь, означает, что с точки зрения специальной теории относительности и в этом случае должно возникнуть отставание часов. Очевидно, что в этом случае, наоборот: Т2 > T3 = T. Получается, что и на самом деле специальная теория относительности делает два взаимоисключающих предсказания Т2 > T3 и Т2 < T3? И это действительно так, если не принять во внимание, что теория была создана для инерциальных систем отсчета. Здесь же движущиеся часы Т2 не находятся в инерциальной системе. Само по себе это не запрет, а лишь указание на необходимость учесть это обстоятельство. И это обстоятельство разъясняет общая теория относительности [2]. Применять его или нет, можно определить простым опытом. В инерциальной системе отсчета на тела не действуют никакие внешние силы. В неинерциальной системе и согласно принципу эквивалентности общей теории относительности на все тела действует сила инерции или тяготения. Следовательно, маятник в ней отклонится, все незакреплённые тела будут стремиться переместиться в одном направлении. Такой опыт рядом с неподвижными часами Т1 даст отрицательный результат, будет наблюдаться невесомость. А вот рядом с движущимися по окружности часами Т2 на все тела будет действовать сила, стремящаяся отбросить их от неподвижных часов. Мы, разумеется, считаем, что никаких иных гравитирующих тел поблизости нет. Кроме того, движущиеся по окружности часы Т2 сами по себе не вращаются, то есть, движутся не так, как Луна вокруг Земли, обращённая к ней всегда одной и той же стороной. Наблюдатели рядом с часами Т1 и Т2 в своих системах отсчета будут видеть удалённый от них на бесконечность объект всегда под одним и тем же углом. Таким образом, движущийся с часами Т2 наблюдатель должен учесть факт неинерциальности своей системы отсчета в соответствии с положениями общей теории относительности. Эти положения говорят, что часы в поле гравитации или в эквивалентном ему поле инерции, замедляют свой ход. Поэтому в отношении неподвижных (по условиям опыта) часов Т1 он должен признать, что эти часы находятся в гравитационном поле меньшей напряженности, поэтому они идут быстрее его собственных и к их ожидаемым показаниям следует добавить гравитационную поправку. Напротив, наблюдатель рядом с неподвижными часами Т1 констатирует, что движущиеся часы Т2 находятся в поле инерционной гравитации, поэтому идут медленнее и от их ожидаемых показаний следует отнять гравитационную поправку. Как видим, мнение обоих наблюдателей полностью совпали в том, что движущиеся в исходном смысле часы Т2 отстанут. Следовательно, специальная теория относительности в «расширенной» трактовке делает два строго согласованных предсказания, что не даёт никаких оснований для провозглашения парадоксов. Это рядовая задача, имеющая вполне конкретное решение. Парадокс в СТО возникает лишь в том случае, если использовать её положения к объекту, не являющимся объектом специальной теории относительности. Но, как известно, неверная посылка может привести как к правильному, так и к ложному результату. Эксперимент, подтверждающий СТО Следует отметить, что все эти рассмотренные мнимые парадоксы соответствуют мысленным экспериментам на основе математической модели под названием Специальная Теория Относительности. То, что в этой модели данные эксперименты имеют полученные выше решения, не обязательно означает, что в реальном физическом эксперименты будут получены такие же результаты. Математическая модель теории прошла многолетнее испытание и в ней не найдено никаких противоречий. Это значит, что все логически корректные мысленные эксперименты неизбежно будут давать результат, подтверждающий её [1]. В этой связи представляет особый интерес эксперимент, который общепризнанно в реальных условиях показал точно такой же результат, что и рассмотренный мысленный эксперимент. Непосредственно это означает, что математическая модель теории верно отражает, описывает реальные физические процессы. Это был первый эксперимент по проверке отставания движущихся часов, известный как эксперимент Хафеле – Китинга, проведённый в 1971 г [3]. Четверо часов, сделанных на основе цезиевых стандартов частоты, были помещены на два самолета и совершили кругосветное путешествие. Одни часы путешествовали в восточном направлении, другие обогнули Землю в западном направлении. Разница в скорости хода времени возникала из-за добавочной скорости вращения Земли, при этом учитывалось и влияние поля тяготения на полетной высоте по сравнению с уровнем Земли. В результате эксперимента удалось подтвердить общую теорию относительности, измерить различие в скорости хода часов на борту двух самолетов. Полученные результаты были опубликованы в журнале Science в 1972 году. Литература 1. Путенихин П.В., Три ошибки анти-СТО, 2011, URL: http://samlib.ru/p/putenihin_p_w/antisto.shtml (дата обращения 12.10.2015) 2. Путенихин П.В., Итак, парадокса (близнецов) больше нет!, 2014, URL: http://samlib.ru/editors/p/putenihin_p_w/ddm4-oto.shtml (дата обращения 12.10.2015) 3. Эксперимент Хафеле-Китинга, Викпиедия, URL: https://ru.wikipedia.org/wiki/Эксперимент_Хафеле_—_Китинга (дата обращения 12.10.2015) 12.10.2015 Адрес полной версии статьи в интернете URL: http://samlib.ru/p/putenihin_p_w/paradox-twins.shtml Иллюстрации и уравнения к статье (зеркала) http://samlib.ru/p/putenihin_p_w/ https://cloud.mail.ru/public/8WpP/qeaUMAiGz https://cloud.mail.ru/public/Hq7e/jZ9YZGJW9 https://yadi.sk/d/EZg36rrKmJDwk https://drive.google.com/folderview?id=0B0uM56-EnG4ZaUFJb0YzY3YtcVU&usp=drive_web http://fileload.info/users/putenikhin/ | |
| Категория: Разное | | | |
| Просмотров: 3301 | Загрузок: 0 | |
| Всего комментариев: 0 | |