Путенихин П.В., Мнимые парадоксы СТО. Парадокс транспортера
| [ Скачать с сервера (286.5 Kb) ] | 09.02.2016, 18:07 |
Путенихин П.В. m55@mail.ru Аннотация Рассмотрен парадокс транспортера специальной теории относительности и его известное решение. Возможно, единственное, либо первое описание и решение парадокса транспортера приводится в работе Соколовского «Теория относительности в элементарном изложении». Сам автор работы указал, что на момент написания книги он не встречал упоминаний об этом парадоксе (здесь и далее цитаты из указанной работы [1]: «Что же касается парадокса транспортера, то ранее он, по-видимому, нигде не анализировался». Отметим, что в цитируемой работе описание и решение парадокса транспортера является исчерпывающим и не вызывает нареканий. Мы обратимся к нему по следующим причинам. Во-первых, при внимательном рассмотрении парадокса транспортера можно заметить его некоторую преемственность от парадокса Белла о тросе и двух ракетах [2]. Во-вторых, есть основания считать, что и сам парадокс транспортера является предшественником парадокса колеса и его разновидности – парадокса Эренфеста. Транспортер представляет собой замкнутую ленту из гибкого материала, которая движется по направляющим с помощью двух шкивов, укрепленных на балке (станине). Как вариант, лента может представлять собой сочленённые жесткие элементы – траки. То есть, в качестве транспортера может рассматриваться обычная гусеница трактора или танка. В нашем случае вариант с траками предпочтительнее, поскольку все релятивистские эффекты можно рассматривать в «чистом» виде, не учитывая растяжения ленты, что делает всю картину существенно более наглядной, в том числе на анимации, становится хорошо заметным движение ленты.  Рис. 1. Транспортер (гусеница трактора) находится в состоянии покоя. Лента транспортера представляет собой сочленённые нерастяжимые элементы – траки. Приведём транспортер в действие с таким расчетом, чтобы скорость движения траков на прямолинейных участках была близка к световой. 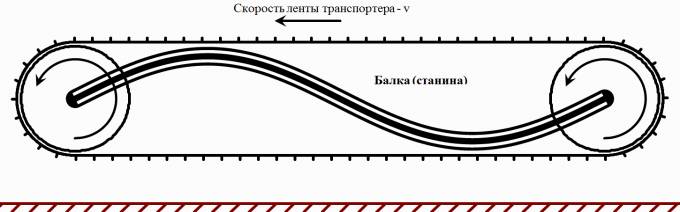 Рис. 2. Траки ленты транспортера движутся на прямолинейных участках со скоростью v, близкой к световой. В системе отсчета балки (станины) движущиеся лента (траки) уменьшит свою длину вследствие лоренцева сокращения. Это приведёт либо к натяжению ленты, если она изначально провисала, вплоть до её разрыва, либо к деформации балки (станины) – её сжатию или изгибу вплоть до поломки. Все эти деформации ленты и станины доступны для физического измерения, они являются объективными. Напротив, в системе отсчета ленты, движущейся оказывается станина, которая и будет подвергнута лоренцеву сокращению: «Если, однако, систему отсчета связать не со станиной, а с лентой, то покоящейся придется считать ленту, а станину — движущейся с большой скоростью. Тогда сократиться должна уже не лента, а станина, результатом чего будет уже не тугое натяжение, а свободное провисание ленты». Естественно, автор приходит к выводу о возникновении противоречия: «Но этот вывод явно противоречит принципу относительности: рассуждения, касающиеся одного и того же явления, в двух разных системах отсчета приводят к взаимно исключающим результатам… Таким образом, мы сталкиваемся с парадоксом: в данном конкретном случае применение теории относительности приводит к отрицанию одной из ее собственных основ – принципа относительности Эйнштейна». Однако, здесь следует заметить, что вывод о возникновении парадокса несколько преждевременный. На этом этапе его формулировки допущена небольшая неточность, недоговоренность. Было явно сказано, что лента не сокращается в своей системе отсчета: «…покоящейся придется считать ленту… сократиться должна уже не лента…». Но это же невозможно оставить без внимания, это очевидно: разные участки ленты движутся с разными скоростями. То есть, в рассматриваемом случае лента не может находиться в покое, и недопустимо использовать при формулировке «парадокса» заведомо неверное обстоятельство. Автор верно отмечает, что на суть парадокса никак не влияют участки ленты на шкивах (катках), их влияние может быть уменьшено до сколь угодно малой величины. Далее он справедливо приходит к заключению, что связать систему отсчета с целой лентой нельзя и нужно рассматривать её как отдельные элементы, что так же не отражается на результате. В нашем варианте с траками последнее заключение становится ещё более очевидным, поскольку мы можем связывать систему отсчета с каждым траком в отдельности или с их группой, движущейся с одинаковой скоростью. Таким образом, пока нельзя говорить о парадоксе, как законченно сформулированном. Поэтому, следующий вывод не вполне точен: «Как и следовало ожидать, рассмотрение в любой действительно инерциальной системе отсчета приводит к одинаковому результату (натяжению ленты). Тем самым парадокс полностью снимается». Парадокс, как таковой, корректно не был сформулирован, поэтому говорить о решении нельзя. Можно говорить об ошибочных предположениях, но никак не о конкретном парадоксе. Скорее всего, здесь наблюдается парадокс формулировки. Вместе с тем, нельзя не согласиться с объяснением, почему укорачивается именно лента (и почему парадокс так и не возник): «… в данном опыте станина и лента физически неравноправны, так как в отличие от станины лента не может считаться покоящейся ни в одной инерциальной системе (потому что ее части движутся друг относительно друга). По этой именно причине укорачивается лента по сравнению со станиной, а не наоборот». Разумеется, речь идёт о ленте, движущейся на транспортере, а не лежащей где-нибудь на складе. Следовательно, говорить о парадоксе не вполне корректно. Он не был сформулирован определённым образом и без ошибок. Данный опыт, поэтому, следует считать не демонстрацией парадокса, а решением обычной, рядовой, хотя и весьма наглядной задачи из курса специальной теории относительности. В нашем варианте с анимацией мы используем ленту, состоящую из траков. Это позволяет наглядно показать все линейные характеристики объектов:  Рис. 3. Нижняя часть ленты транспортера неподвижна. Балка (станина) движется со скоростью v, a верхняя часть ленты – с удвоенной скоростью 2v, близкой к световой. Допустим, длина ленты, как сумма длин составляющих её траков, в состоянии покоя равна L0. Для простоты примем, что длина участков ленты, находящихся на шкивах (катках) во много раз меньше длины прямолинейных участков и может быть принята равной нулю. Мы исходим в этом из рассуждений автора, которые считаем вполне справедливыми. Рассмотрим состояние транспортера в случае неподвижной балки (станины), в её системе отсчета. Очевидно, что верхняя и нижняя части ленты движутся с одинаковой скоростью и сократятся в одинаковое число раз. Сокращаясь, лента притянет шкивы (катки) друг к другу. В процессе этого балка (станина) будет деформирована, она либо изогнётся, либо разрушится, переломится. Напротив, в системе отсчета, например, нижней части ленты, будут сокращаться уже сама балка и верхняя часть ленты. Известно, что при движении балки со скоростью v верхняя часть ленты будет двигаться с удвоенной скоростью 2v. Следовательно, длина балки в этом случае будет равна: 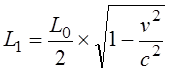 Здесь учтено, что в состоянии покоя длина балки равна половине длины ленты. Длины верхней и нижней частей ленты будут равны друг другу, поскольку в случае разности их длин, более короткая часть будет «перетягивать» к себе недостающее число траков из другой части. В этом случае условная длина участков в неподвижном состоянии может быть обозначена как L0t (top – верхняя) и L0b (bottom – нижняя). Примем, что L0t = kL0b. Понятно, что L0 = L0t+L0b = L0b(k+1). После достижения скорости балки v длины верхней и нижней частей ленты будут равны: 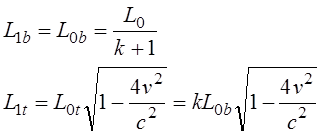 Поскольку они равны: 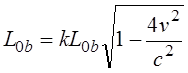 Откуда находим величину k: 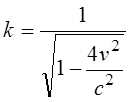 Следовательно, величина L1t = L0b, до которой будут стянуты катки, равна: 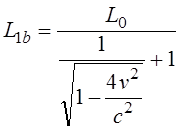 Вот теперь мы можем говорить о возможности более корректной формулировки парадокса. Если величина L1 – сокращение балки окажется меньше, чем L1b – сокращение расстояния между катками из-за сокращения ленты, то лента не натянется, а провиснет. Сравним эти две вычисленные величины, найдя их отношение:  Произведя тривиальные преобразования, находим: 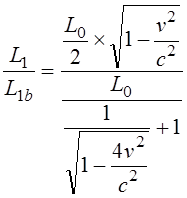 Все три выражения с корнями являются монотонно убывающими функциями (не имеющими экстремумов и разрывов) на диапазоне от нуля до с. Легко получить граничные значения данного выражения. При нулевой скорости выражение равно: 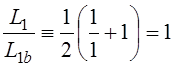 При увеличении удвоенной скорости до скорости света, значение выражения стремится к бесконечности: 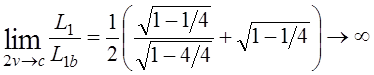 Следовательно, значение данной функции на всём диапазоне не имеет значений меньше 1, то есть, длина балки (станины) при всех скоростях движения всегда оказывается больше, чем расстояние между «стянутыми» лентой катками. Это означает, что либо балка будет деформирована, либо лента порвётся (растянется, если она эластичная). Например, при скорости 2v=0,866c траки верхней части ленты сократятся ровно в два раз. Скорость балки при этом равна v=0,433с. Значение полученного выражения будет: 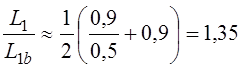 То есть, в этом случае лента транспортера будет стремиться сжать балку до уменьшения её длины почти в полтора раза. Таким образом, и в данном случае сформулировать парадокс транспортера не удалось. В обоих случаях, и с точки зрения балки (станины) и с точки зрения любого трака или группы траков, образующих, например, нижнюю часть ленты, результатом будет натяжение ленты, приводящее либо к деформации сжатия, изгиба или слома станины, либо к деформации натяжения вплоть до разрыва ленты. В зависимости от начальных условий: что будет задано более прочным. Парадокс транспортера оказался мнимым, кажущимся парадоксом. Выше я отметил, что эта задача имеет некоторое сходство другими парадоксами. Речь идёт не о прямой хронологической последовательности, а, скорее, об идейной преемственности. Почему задача Белла об ускоренно движущихся ракетах, соединённых тросом кажется, предшественником? В обеих задачах мы имеем дело с двумя жестко скрепленными движущимися объектами, которые имеют при этом различное лоренцево сокращение. Но в задаче Белла это сокращение рассматривается в более широком смысле: один из этих объектов - «тандем двух ускоренно движущихся ракет» принудительно компенсирует, устраняет собственное лоренцево сокращение. Относительно парадокса колеса и парадокса Эренфеста можно сделать такое наблюдение. Если смотреть на колесо под большим углом, почти «с ребра», то оно будет выглядеть как сильно вытянутый эллипс. Все наблюдаемые в парадоксе транспортера эффекты будут, видимо, проявляться весьма схожим образом. Можно ожидать, что объяснение этих парадоксов также окажется преемственным. Литература 1. Соколовский Ю.И. Теория относительности в элементарном изложении. – М.: Наука, 1964 2. Путенихин П.В. Мнимые парадоксы СТО. Теорема Белла, [рассмотрен парадокс Белла, в котором две ракеты, соединенные тросом, движутся с одинаковым ускорением. Трос со временем разрывается], URL: http://samlib.ru/p/putenihin_p_w/paradox-bell.shtml 03.10.2015 Адрес полного текста статьи в интернете URL: http://samlib.ru/p/putenihin_p_w/paradox-transp.shtml Иллюстрации и уравнения к статье (зеркала) http://samlib.ru/p/putenihin_p_w/ https://cloud.mail.ru/public/8WpP/qeaUMAiGz https://cloud.mail.ru/public/Hq7e/jZ9YZGJW9 https://yadi.sk/d/EZg36rrKmJDwk https://drive.google.com/folderview?id=0B0uM56-EnG4ZaUFJb0YzY3YtcVU&usp=drive_web http://fileload.info/users/putenikhin/ | |
| Категория: Разное | | | |
| Просмотров: 3659 | Загрузок: 79 | |
| Всего комментариев: 0 | |