Путенихин П.В., Не-белловские квантовые запутанные состояния
| [ Скачать с сервера (469.4 Kb) ] | 08.02.2016, 21:55 |
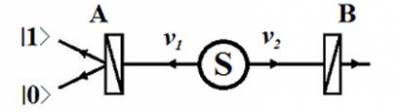
Полный текст статьи находится в прилагаемом файле. Ниже приведён фрагмент текста для ознакомления. Путенихин П.В. m55@mail.ru Аннотация Данная работа посвящена исследованию состояний квантовой запутанности общего вида (не-белловских состояний запутанности) и их созданию с помощью квантового гейта CNOT. Рассмотрены переходы друг в друга при повороте запутанных состояний Белла и логическая сущность нелокальности на примере мысленного эксперимента с квантовым «нелокальным кубиком». В квантовой механике известны состояния квантовых частиц с уникальными нелокальными свойствами – так называемые состояния полной запутанности – состояния Белла: 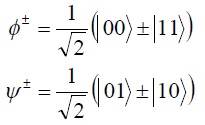 Два из этих состояний в литературе известны под собственными именами: ψ- - «ЭПР-состояние» и ϕ+ - «состояние шредингеровского кота». Частицы в состоянии запутанности ведут себя как единое целое независимо от расстояния между ними, демонстрируя полную и мгновенную взаимосвязь. Однако, приведённые четыре состояния Белла – это лишь часть всех возможных состояний запутанности, их частный случай. В общем виде состояния запутанности могут быть представлены следующими уравнениями: 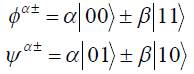 Исследованию этих состояний посвящена данная работа. Содержание Как создаются запутанные состояния. Гейт CNOT Почему 00+11? Взаимные превращения запутанных состояний Белла Математическое исследование не-белловского состояния в общем виде Логика и философия нелокальности * * * Чтобы увидеть удивительно согласованное поведение запутанных частиц, а также некоторые отличия в поведении частиц в не-белловских состояниях от поведения частиц в чистых состояниях Белла, проведём математическое исследование не-белловских состояний на мысленной экспериментальной установке: На изображенной установке частицы v1 и v2 от источника запутанных фотонов S поступают двум исследователям: A - Алисе и B - Бобу. Алиса, вращая свой двухканальный (расщепляющий) поляризатор, изменяет состояния квантовых частиц на стороне Боба вследствие их запутанности. Не используя классические каналы связи, Боб попробует определить направление поляризатора Алисы. Ещё до проведения математического анализа можно сделать очевидное предсказание: никакие действия Алисы не могут создать на стороне Боба состояния, по которым Боб смог бы узнать о действиях Алисы. Как создаются запутанные состояния. Гейт CNOT Явление запутанности непосредственно следует из математического формализма квантовой механики. В соответствии с первым постулатом квантовой механики состояние квантовой частицы полностью описывается её волновой функцией. Однако, в некоторых случаях некоторым квантовым частицам не удаётся приписать собственные волновые функцию, а только одну на всех. Такое состояние частиц названо запутанностью. Это состояние удалось получить на реальных частицах, например, в так называемых процессах параметрического распада, преобразования с понижением частоты (down conversion) на специальных кристаллах. Помимо параметрического распада для получения состояния запутанности используются квантовые гейты CNOT. Математическое описание этого процесса очень наглядно и просто. Рассмотрим его. Схематично гейт CNOT можно изобразить следующим образом: 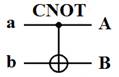 Математически этот квантовый оператор дается выражением: 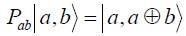 где знак плюс в окружности означает логическое сложение по модулю 2. (Полный текст статьи находится в прилагаемом файле) 07.11.2013 Адрес полного текста статьи в интернете URL: http://samlib.ru/p/putenihin_p_w/non-bell.shtml Иллюстрации и уравнения к статье (зеркала) http://samlib.ru/editors/p/putenihin_p_w/ https://cloud.mail.ru/public/8WpP/qeaUMAiGz https://cloud.mail.ru/public/Hq7e/jZ9YZGJW9 https://yadi.sk/d/EZg36rrKmJDwk https://drive.google.com/folderview?id=0B0uM56-EnG4ZaUFJb0YzY3YtcVU&usp=drive_web http://fileload.info/users/putenikhin/ | |
| Категория: Разное | | | |
| Просмотров: 3228 | Загрузок: 81 | |
| Всего комментариев: 0 | |