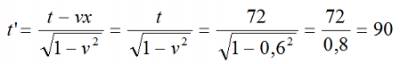Путенихин П.В., Динамические диаграммы Минковского - обмен сверхсветовыми сигналами
| [ Скачать с сервера (2.66 Mb) ] | 08.02.2016, 19:41 |
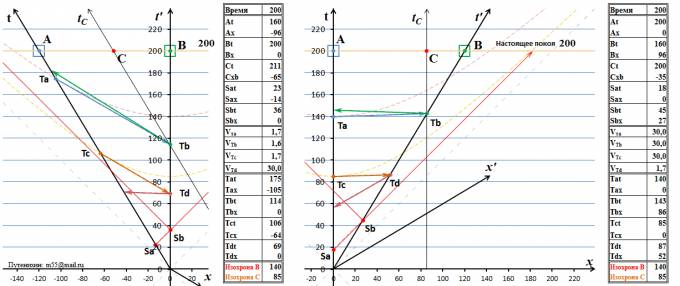
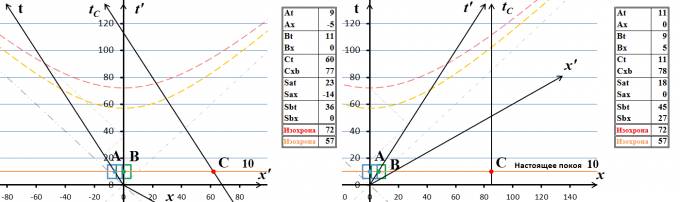
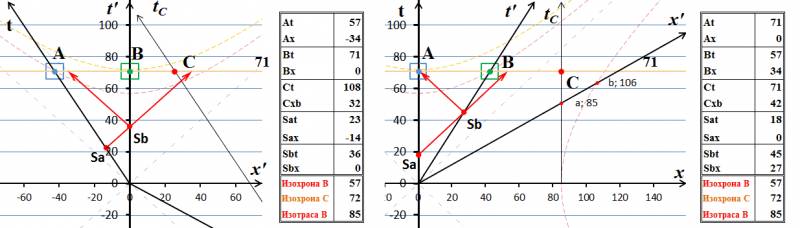
Путенихин П.В. m55@mail.ru Аннотация Специальная теория относительности в области сверхсветовых скоростей приводит к противоречивым предсказаниям и нарушению причинности. С данной работе подвергнут критическому анализу главный инструмент специальной относительности для сверхсветовых сигналов – принцип реинтерпретации. На примере динамических диаграмм Минковского показана его противоречивость, его антилогичные, не физические выводы. Специальная теория относительности неприменима к сверхсветовым движениям. Статья содержит gif-анимации. С 1908 года диаграммы Минковского используются для наглядной демонстрации различных ситуаций в рамках специальной относительности. По сравнению с аналитическими выкладками диаграммы позволяют более отчётливо увидеть кинематические эффекты теории. Следующим шагом повышения наглядности представления релятивистских эффектов следует считать их анимационное представление, показ этих эффектов в движении, в динамике. Для этих целей диаграммы могут быть представлены как в классическом виде, так и с динамическим масштабированием. В последнем случае масштаб диаграммы непрерывно увеличивается с течением времени, в результате чего появляется возможность рассматривать неограниченные временные и пространственные интервалы. В данной работе мы воспользуемся первым, классическим вариантом динамических диаграмм Минковского, с неизменным масштабом. Ситуация, которую мы будем рассматривать, относится к довольно спорной области теории относительности – обмену сверхсветовыми сигналами. Носителями таких сигналов могут быть частицы из семейства тахионов, квантино (предложен Вейником), информион (так может быть названа частица, передающая квантовую информацию при коллапсе запутанных частиц), ньютион (такое название частице можно дать, чтобы подчеркнуть её антагонизм специальной теории относительности). Суть сверхсветового агента не важна. Единственное важное для нас его свойство – это его способность быть зарегистрированным в процессе сверхсветового движения. Сначала давайте посмотрим на один из вариантов анимированных диаграмм Минковского для трёх различных случаев обмена сигналами между движущимися системами отсчета, а затем дадим описание всем изображённым на них элементам. Все приведённые с в статье анимации можно увидеть по ссылкам внизу статьи и в прилагаемом файле. Следует отметить, что динамические диаграммы выполнены в формате gif-файлов с оптимизацией в целях уменьшения их объёма. К сожалению, такие оптимизированные файлы некоторыми браузерами отображаются не вполне корректно. Например, браузер Интернет-эксплорер версии 8 и 9 «смазывает» изображение и замедляет его отображение. Но браузеры ИЕ-11 и firefox отображают эти динамические файлы без каких-либо дефектов. Поэтому, если отображение происходит со «смазыванием», то следует воспользоваться другим браузером. Все анимационные файлы «зациклены», то есть воспроизводятся повторно неограниченно долго, что позволяет внимательно рассмотреть и описать все происходящие на них процессы. Рис.1 Динамические диаграммы Минковского для случаев обмена световыми и сверхсветовыми сигналами. Приведены диаграммы с точки зрения двух наблюдателей: слева – система покоя наблюдателя B, справа – наблюдателя A. На диаграммах координатные оси имеют градации в долях от скорости света в системе единиц, в которой сама скорость света приравнена единице, то есть c=1. По этой причине вертикальная ось диаграмм имеет обозначение t вместо классического обозначения ct. Однако, размерностью этой оси являются, тем не менее, не секунды, а метры, хотя ось и обозначена как ось времени (м/сек * сек = м). Все уравнения Лоренца при таком значении скорости света записываются в более простой форме, без многоэтажных дробей. При этом скорости всех объектов будут измерять в долях скорости света. Например, классические уравнения преобразований Лоренца примут следующий вид: 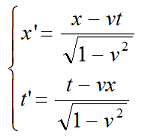 Понятно, что в этом случае абсолютное значение скорости для движущихся объектов будет не больше единицы. На диаграммах показано относительное движение двух систем отсчета – А и В. Слева на рисунке ситуация изображена с точки зрения системы В, которая в данном случае является лабораторной, условно неподвижной ИСО. Справа на рисунке системой покоя является система А. В рассматриваемом случае мы задали скорость относительного движения систем равной 0,6с или, для принятых допущений, просто 0,6. Эта скорость интересна с той точки зрения, что значение корня оказывается в точности равным 0,8. Диапазон рассматриваемого на диаграмме движения составляет 220 секунд, а расстояния – чуть более 220 световых секунд. Световая секунда, как можно догадаться, это расстояние, которое свет проходит за 1 секунду, это примерно 70 миллионов километров. Картина ничуть не изменится, если принять, что оси размечены в световых годах. В системе отсчета А находится вспомогательный наблюдатель С, который, понятно, является неподвижным в этой системе. Движение всех наблюдателей в пространстве-времени Минковского описывается их мировыми линиями. На рисунке таких линий три. Мировую линию системы А мы обозначим осью t. По этой причине на рисунке справа она строго вертикальна, ведь движения в собственной, связанной с ней самой системе у неё нет. Такой же вертикальной линией (на рисунке она имеет координату 85 световых секунд) является и мировая линия наблюдателя С – tC. Напротив, на левой половине рисунка они наклонны. Мировая линия движущейся системы отсчёта В изображена осью t'. Все движущиеся системы имеет угол наклона своих мировых линий к оси времени, тангенс угла которых в указанных координатах точно равен скорости движения этой системы. Для системы В тангенс угла наклона, как мы задали, равен 0,6 на правой стороне рисунка. На левой стороне такой наклон имеют мировые линии наблюдателей А и С. Ещё две пересекающиеся мировые линии изображены на обеих сторонах рисунка черными тонкими штриховыми линиями. Это мировые линии света, они наклонены к вертикальным осям под углом в 45 градусов. В трёхмерном варианте диаграмм они образуют два так называемых световых конуса - будущего и прошлого. Мировые линии всех движущихся систем отсчета находятся внутри этих конусов. Для удобства анализа состояния систем на диаграммах показаны также и другие вспомогательные линии. Основная из них – это линия «настоящее время системы покоя» или, кратко, «настоящее покоя». Эта линия изображена оранжевым цветом, надписью и числовым отображением времени, соответствующего настоящему времени системы покоя. Все события, которые могут произойти в неподвижной системе отсчёта могут находиться только на этой линии настоящего. Напротив, все события ниже этой линии уже произошли и находятся в прошлом. Все события выше этой линии ещё не произошли, они – события будущего. На диаграмме красными тонкими штриховыми линиями изображены ещё две вспомогательные линии - изохроны и изотрасы. Это линии, соответственно, равных времён и равных расстояний. Они позволяют сравнить ход времени во всех системах отсчёта, нанесённых на диаграмму, обнаруживая при этом все лоренцевы кинематические эффекты: замедление времени, сокращение расстояний и относительность одновременности. Справа от каждой диаграммы приведена таблица со значениями основных параметров движения систем и свершения событий. Заглавными буквами обозначены, соответственно, А, В и С – инерциальные системы отсчета одноименных наблюдателей. Индексы t и x означают соответствующую координату этих систем отсчета. В зависимости от диаграммы координаты времени отражают течение времени внутри системы с точки зрения неподвижной, лабораторной системы отсчета, если не указано иное для конкретной диаграммы. Для системы С представляют интерес и показаны на некоторых диаграммах только её координаты с точки зрения системы В, поскольку в системе А она неподвижна. Через V с индексами a, b, c и d обозначены скорости одноименных индексам тахионов. Через S с индексами a и b обозначены события излучения световых сигнала и ответа на сигнал, соответственно. Изохроны и изотраса обозначены координатами своих точек, ближайших к началу координатных осей. Для наглядности на некоторых диаграммах тонкими штриховыми линиями обозначены трассы сигналов – тахионов и света. Более подробно при необходимости эти значения мы опишем при рассмотрении отдельных моментов движения. На показанной выше анимации динамических диаграммах Минковского можно выделить три отдельных, независимых процесса или этапа. Опишем эти процессы подробнее. Обмен световыми сигналами между движущимися системами Этот процесс является простой демонстрацией динамических диаграмм и не несёт особо сложной смысловой нагрузки: Рис.2 Обмен световыми сигналами между движущимися системами. Приведены диаграммы с точки зрения двух наблюдателей: на правой половине – с точки зрения системы покоя наблюдателя А, на левой – наблюдателя В. На этих диаграммах оставлены только мировые линии световых сигналов, которые обозначены красными стрелками. В момент времени Sa=18с из неподвижной системы отсчета А излучается световой сигнал в сторону системы В. Когда сигнал в момент времени Sb=45с достигает системы В, оттуда излучается ответный сигнал, который, как можно увидеть на диаграмме, достигает системы А в момент времени примерно 72с, что видно по изохроне 72: точка её пересечения с мировой линией А показывает на последней время 72. Далее основной и ответный сигналы продолжают свободное движение в пространстве, удаляясь от систем А и В в разные стороны. Например, в момент времени приблизительно 102с по собственным часам сигнал достигает третьего наблюдателя – С. Может возникнуть вопрос: приблизительно в этой точке мировую линию С также пересекает изохрона 72, почему же время события 102с, а не 72? Потому, что изохроны отсекают «своё время» только на мировых линиях, исходящих из начала координат. Ситуация, как видим, является тривиальной, и весь смысл динамической диаграммы состоит в её наглядности. На этой диаграмме изохрона 72 совмещена с точкой получения системой А ответного сигнала. Поскольку изохрона – это линия равных времён, то в данном случае это означает, что по часам системы В поглощение произошло в 72с, в то время как по часам А – примерно в 90с. Это точно соответствует решению уравнений Лоренца: Если на рис.1 измерить отрезки, отсекаемые на оси x' мировой линией tC и изотрасой, то можно найти, что с точки зрения подвижной системы В наблюдатель С находится от начала координат на расстоянии: x'C = x'C∙√(1-v2) = 85 x 0,8 = 68 световых секунд То же самое по точкам на диаграмме: x'C = x'C∙0а/0b = 85 x (85 / 106) = 68 световых секунд Нужно отметить, что мировые линии света имеют один и тот же неизменный наклон в обеих системах отсчета, то есть одну и ту же скорость. Это является отражением второго постулата специальной теории относительность об инвариантности скорости света во всех системах отсчета. Напротив, мировые линии движущихся систем отсчета изменяют свой наклон при переходе в другую систему отсчета. Рис.3 Обмен световыми сигналами между движущимися системами. Время прибытия ответного сигнала не зависит от точки зрения. Обратите внимание на время регистрации ответного сигнала в системе А. На рисунке, казалось бы, несоответствие: с точки зрения системы А (справа) сигнал уже прибыл в неё, но с точки зрения наблюдателя В (слева) сигнал ещё в пути. Однако, никакого несоответствия нет. В лабораторной системе А сигнал зарегистрирован в 72 секунды по её часам. При этом часы системы В показывают с точки зрения А время 58 секунды. Если рассматривать ситуацию для этого же времени из лабораторной системы В на левой стороне рисунка, то мы видим, что часы А показывают с её точки зрения лишь 58 секунд. То есть по часам А ещё не наступило время регистрации ответного сигнала. (Полный текст статьи находится во вложении) Вывод: сверхсветовой канал связи вынуждает специальную теории относительности делать взаимоисключающие предсказания для одной и той же ситуации. Теория, которая даёт такие противоречивые предсказания, являет ложной теорией. В данном случае ложной является расширенная сверхсветовыми движениями специальная теория относительности. 29.03.2014 Адрес полного текста статьи в интернете URL: http://samlib.ru/p/putenihin_p_w/ddm-ftl.shtml Иллюстрации и уравнения к статье (зеркала) http://samlib.ru/editors/p/putenihin_p_w/ https://cloud.mail.ru/public/8WpP/qeaUMAiGz https://yadi.sk/d/EZg36rrKmJDwk | |
| Категория: Разное | | | |
| Просмотров: 3618 | Загрузок: 99 | |
| Всего комментариев: 0 | |