Путенихин П.В., Взаимные переходы квантовых состояний Белла
| [ Скачать с сервера (517.3 Kb) ] | 08.02.2016, 15:25 |
Путенихин П.В. m55@mail.ru Аннотация Приведён анализ свойств запутанных частиц (состояний Белла). Показано, что после поворота гейтом Адамара белловских состояний два из них переходят друг в друга Как известно, чистые запутанные состояния частиц описываются четырьмя так называемыми состояниями Белла, которые имеют следующий вид:  Два из этих состояний в литературе имеют собственные названия. Одно из них:  Это «ЭПР-состояние», название, возникшее исторически в связи с вопросом о полноте квантовой механики, поднятым Эйнштейном, Подольским и Розеном. Другое состояние, называемое в литературе «Состоянием шредингеровского кота» не имеет чёткого обоснования:  Оба эти состояния имеют отличительную особенность от двух других. Они сохраняют свои состояния, соответственно, ортогональности и коллинеарности при поворотах. То есть, вращение сдвоенных поляризаторов, измеряющих эти пары фотонов, всегда дают результат, показывающий, что эти пары частиц, соответственно, ортогональные или коллинеарные. В отличие от них, два других состояния Белла при таких измерениях переходят друг в друга. То есть при одном угле измерения пара частиц ведёт себя как коллинеарная, при других углах - как ортогональная. Чтобы показать это, произведём вращение каждой из пар запутанных фотонов с помощью гейта Адамара:  Фотон, прошедший через гейт Адамара, изменяет направление своей поляризации таким образом, что она поворачивается в пространстве на угол 45о. Посмотрим, что происходит с запутанной парой, когда оба фотона проходят через такой гейт. Состояние «шредингеровского кота» использовал в своих экспериментах Ален Аспект, чтобы показать, что запутанные фотоны в строгом соответствии с математикой квантовой механики нарушают неравенства Белла даже в случае, если состояние поляризаторов изменяется «в полёте». Это состояние наиболее удобно для таких экспериментов, поскольку коллинеарная связь фотонов сохраняется для любых углов поляризаторов в пространстве. Оно имеет вид:  Измерение одного из фотонов с равной вероятностью даёт состояние |0> или |1>. Если второй фотон измеряется поляризатором, параллельным первому поляризатору, то с вероятностью 1 будет получен результат, совпадающий с первым измерением. Если поляризаторы поворачивать, оставляя их всегда параллельными (коллинеарными) друг другу, то всегда будут получены совпадающие результаты измерений: оба измерения дадут либо |0>, либо |1>. Вместо поворота поляризаторов можно поворачивать запутанные фотоны. Это можно сделать, например, пропустив оба фотона пары через соответствующие гейты Адамара. В этом случае мы получим: 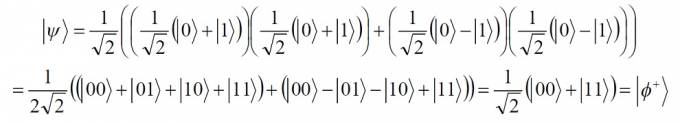 Как видим, при повороте фотонов, волновая функция, описывающая их состояние, не изменила своего вида. Крайне условно, лишь для ассоциаций можно изобразить это состояние и поворот следующим образом:  Каждый из фотонов пары показан собственной стрелкой, как одиночный фотон: один - синим цветом, другой - красным. Волновая функция ф+ на рисунке представляет собой равновероятную суперпозицию двух запутанных состояний. Как известно, волновая функция равновероятной суперпозиции двух состояний одиночного фотона имеет похожий вид - в этом случае в дираковских скобках указывается только одна цифра - 1/√2(|0>+|1>). Такой единичный фотон находится в собственном состоянии. Понятно, что изображение запутанных фотонов на рисунке является условным, схематичным, поскольку запутанные фотоны не имеют определённой поляризации. Такая же в точности картина будет наблюдаться и для ЭПР-состояния:  Как и в предыдущем случае изобразим его в крайне условном графическом виде:  В отличие от «ЭПР-состояния» в этом случае фотоны имеют ортогональные (синглетные) поляризации. Это значит, что измерив один из фотонов, мы получим с равной вероятностью состояние |0> или |1>. Последующее измерение ортогональным (или коллинеарным) поляризатором второго фотона с единичной вероятностью даст ортогональное к первому состояние |1> или |0>, соответственно. По этой причине фотоны пары также условно изображены двумя ортогональными цветными стрелками, формально описываемыми волновыми функциями 1/√2(|0>+|1>) и 1/√2(|1>-|0>), хотя, как и выше, фотоны на самом деле не имеют определённых состояний. Как и в предыдущем случае, вращение поляризаторов или фотонной пары не изменяет результатов измерений. Действительно, пропустив каждый из синглетных фотонов через свой гейт Адамара, мы получим: 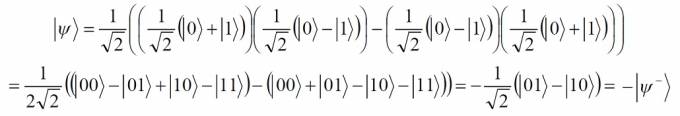 Знак минус перед волновой функцией является фазовым множителем и не влияет на результаты измерений. То есть, при повороте фотонов в ЭПР-состоянии мы получили то же самое ЭПР-состояние. Совершенно иная картина будет наблюдаться при повороте двух оставшихся состояний Белла. Одно из них напоминает состояние «шредингеровского кота»:  Как и фотоны в состоянии шредингеровского кота, фотоны в этом состоянии при измерении поляризаторами в измерительном базисе будут давать одинаковые результаты. Если один из фотонов каждой из пар будет зарегистрирован в состоянии |0>, то и второй также будет зарегистрирован в состоянии |0>. Если один из фотонов пар будет зарегистрирован в состоянии |1>, то и второй фотон пары тоже будет зарегистрирован в этом же состоянии. То есть базисные поляризаторы всегда будут давать коллинеарный результат измерений. Однако, если повернуть поляризаторы на 45o или, что то же самое, повернуть на этот угол оба фотона пары, мы получим иной результат. После поворота фотонов они будут описываться другой волновой функцией: 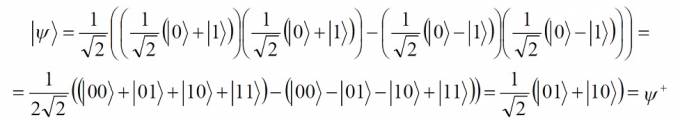 Этот переход можно изобразить (опять же крайне условно) графически: 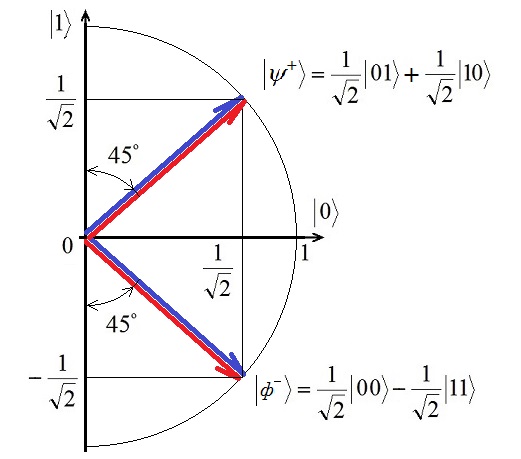 Как и ранее, на рисунке нижней парой стрелок условно показана фотонная пара в состоянии ф- - до поворота гейтом Адамара, а верхней парой стрелок - в состоянии ψ+, после поворота гейтом. Как видим, эта волновая функция ψ+ описывает синглетное состояние фотонов, то есть взаимно перпендикулярные направления поляризации: если один из фотонов пары будет измерен поляризатором и обнаружен в состоянии |0>, то второй фотон пары обнаружен в состоянии |1>. И наоборот. Фотоны, изначально бывшие в измерительном базисе коллинеарными, после поворота оказались в ортогональном состоянии запутанности. Следует заметить, что если бы такого превращения при повороте запутанной пары не было, то можно было бы осуществить сверхсветовую передачу классической информации с использованием гейта CNOT. Теперь посмотрим, что будет с этой запутанной парой, если её повернуть ещё на 45o. Это также означает: что будет с оставшимся состоянием Белла, если его повернуть на этот угол:  После прохождения фотонов пары через гейт Адамара, они будут описываться новой волновой функцией (исходной, если считать, что это двойным поворотом пары): 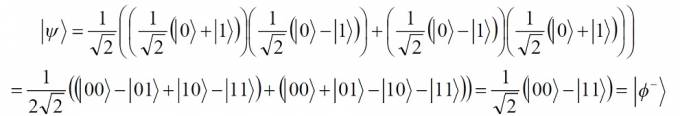 Как видим, если до поворота запутанные фотоны находились в ортогональном (синглетном) состоянии запутанности, то после поворота они (вновь) оказались в коллинеарном состоянии. В первом случае измерение фотонов давало ортогональные поляризации фотонов, во втором (после поворота) - измерения будут давать коллинеарные результаты. Этот переход условно показан графически на том же последнем рисунке. Можно предположить, что существует промежуточное положение (угол поворота поляризаторов), в котором фотоны будут демонстрировать вообще отсутствие корреляции! Полученный результат является весьма примечательным. Ортогонально-коллинеарное поведение запутанных фотонов является фундаментальной причиной невозможности передачи информации чисто математическими средствами: при любом измерении фотонов на одной стороне, на другой образуются два ортогональных потока, причём любой дисбаланс одного из этих потоков всегда компенсируется вторым. То есть, уменьшение прохождения фотонов одного потока через данный поляризатор будет восполнено (компенсировано) увеличением прохождения через него же фотонов из ортогонального потока. Квантовая механика только описывает, но не предлагает никакого объяснения явлению корреляции (нелокальности). Между запутанными частицами явно просматривается информационная связь, которая в принципе не может существовать без физического носителя. Математическое описание этой связи верное, но никакая информация не может быть передана без физического носителя, будь то частица, поле, волна и т.п. Только выявление этого носителя и создание способов его регистрации может позволить использовать запутанность для передачи информации. 02.11.2013 Адрес полного текста статьи в интернете URL: http://samlib.ru/p/putenihin_p_w/prevrash.shtml Иллюстрации и уравнения к статье (зеркала) http://samlib.ru/p/putenihin_p_w/ https://cloud.mail.ru/public/8WpP/qeaUMAiGz https://yadi.sk/d/EZg36rrKmJDwk | |
| Категория: Разное | | | |
| Просмотров: 3492 | Загрузок: 75 | |
| Всего комментариев: 0 | |