Путенихин П.В., Анализ выводов Белла по парадоксу Эйнштейна Подольского Розена
| [ Скачать с сервера (268.9 Kb) ] | 05.02.2016, 21:10 |
Путенихин П.В. m55@mail.ru Аннотация Статья Белла «On the Einstein Podolsky Rosen paradox» явилась убедительным математико-логическим опровержением доводов Эйнштейна о неполноте квантовой механики и сформулированных им положений так называемого «локального реализма». Со дня опубликования статьи в 1964 году и до наших дней доводы Белла, более известные в форме «неравенств Белла», служат самым распространённым и главным аргументом в споре между представлениями о нелокальности квантовой механики и целым классом теорий на основе «скрытых переменных» или «дополнительных параметров». В предлагаемой работе высказаны предположения, что возражения Белла являются компромиссом между специальной теорией относительности и экспериментально наблюдаемым явлением запутанности, имеющим все видимые признаки мгновенной зависимости двух отделенных друг от друга систем. Этот компромисс известен в наши дни как нелокальность или несепарабельность. Нелокальность фактически отрицает положения традиционной теории вероятности на зависимые и независимые события и обосновывает новые положения – квантовую вероятность, квантовые правила вычисления вероятности событий (сложение амплитуд вероятностей). Подобный компромисс служит почвой для возникновения мистических взглядов на природу. Вместе с тем, если тщательно проанализировать доводы Белла, то можно обнаружить и «сопутствующие» выводы из его статьи. Известное утверждение Эйнштейна о том, что квантовая механика неполна, получает достаточно заметное основание. Суть этого утверждения можно выразить развернутой фразой: «современная физика, превратилась, по сути дела, в продолжение математики, совершенно утратив все надежды на понимание природы изучаемых явлений». Собственно, цель, заявленная самим Беллом в статье, не столько утверждение или подтверждение полноты квантовой механики, сколько логическое опровержение идеи локальности: «Парадокс Эйнштейна, Подольского и Розена [ссылка 1] был выдвинут как аргумент того, что квантовая механика – теория не полная и в нее должны быть включены дополнительные переменные. Эти дополнительные переменные должны были вернуть в теорию причинность и локальность [ссылка 2]. Отметим, что идея будет сформулирована математически и будет показано, что она несовместима со статистическими предсказаниями квантовой механики». [2] В этой связи отметим главное и основное содержание работы Белла: нелокальная связь между запутанными частицами не может быть описана как вероятностная, статистическая. Другими словами: между частицами имеется чётко выраженная связь, однозначно определённая зависимость между их состояниями. Однако, Белл отказывается признать это очевидное обстоятельство, придерживаясь постулатов теории относительности: «Главную трудность создает требование локальности, означающее, что результат измерения на одной системе не может зависеть от действий на отдаленной системе, с которой она взаимодействовала в прошлом». [2] Он прямо и недвусмысленно выражает озабоченность локальностью. Другими словами: известно, что состояния двух частиц строго коррелированы, причём независимо от расстояния и времени [1], но признать корреляцию как результат взаимодействия не позволяет теория относительности. Информация о взаимодействии в прошлом (в виде дополнительных переменных) не позволяет объяснить эту корреляцию, что, собственно, Белл и доказывает в своей работе. Мы не будем здесь рассматривать все выкладки Белла, лишь напомним его заключительное выражение, которое в последствии «превратилось» в многочисленные варианты «неравенств Белла». Это следующее выражение (здесь и далее значки векторов опущены): 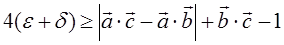 и вывод, сделанный на его основе для частного случая: «Как видим, для любого малого конечного δ, ε не может быть произвольно малым». [2] Данное выражение (22), собственно, и следует считать оригинальной версией «неравенств», смысл которых сводится к утверждению, что связь между запутанными частицами с использованием «дополнительных переменных» не может быть описана как вероятностная. В заключении работы Белл делает вывод: «В квантовой теории с дополнительными параметрами для того, чтобы определить результаты индивидуальных измерений без того, чтобы изменить статистические предсказания, должен быть механизм, посредством которого настройка одного измеряющего устройства может влиять на чтение другого отдаленного инструмента. Кроме того, задействованный сигнал должен распространяться мгновенно так, что такая теория не может быть лоренц-инвариантом» [2]. Итак, согласно выводу Белла, для того чтобы «полная» квантовая теория делала такие же статистические предсказания, как и традиционная, необходим механизм взаимодействия между измерителями. К такому выводу он пришёл, последовательно и неуклонно следуя исходному положению Эйнштейна: предсказания «полной» квантовой механики должны быть статистическими, вероятностными. Здесь под «полной» квантовой механикой подразумевается теория, отвечающая высказыванию Эйнштейна: «Хотя мы и показали, что волновая функция не даёт полного описания физической реальности, мы оставили открытым вопрос о том, существует ли такое описание или нет. Мы думаем, однако, что такая теория возможна» [7], или теория, включающая в себя «дополнительные параметры». В этой связи напомним высказывание Алена Аспекта: «Эйнштейн на самом деле не говорил о «скрытых переменных» или «дополнительных параметрах», а скорее об «элементах физической реальности». Соответственно, многие авторы говорят скорее о «реалистических теориях», а не о «теориях со скрытыми переменными» или «теориях дополнительных переменных». [1] Полученные Беллом выводы отвергают возможность получения таких вероятностных результатов при наличии одних только «дополнительных переменных». Поэтому делается приведённый выше вынужденный вывод о связи между измерителями. Однако, что это означает? Предположим, что получен некий результат измерения на ближней системе. Если бы он был случайным, вероятностным, не связанным с действиями над удаленной системой, то это был бы результат А. Но на самом деле получен результат другой – В. А именно, результат, который не может рассматриваться как случайный! Этот результат отражает как бы зависимость от измерения на удаленной системе, он с этим результатом имеет, пусть кажущуюся, но всё-таки связь, связь более значимую, чем традиционная случайность. Этот результат можно представить как подбрасывание монеты, при падении которой орёл выпадает, например, в два раза чаще, чем решка. Очевидно, что результаты орёл и решка в данном случае не равновероятны, и выпадение одного из них явно связано с особенностями монеты, стола или с хитростью исследователя. Какова же причина такого результата измерения на ближней системе? Рассмотрим возможные варианты. Например, результат В возник из-за того, что измеритель на удалённой системе передал сигнал измерителю на ближней системе и тот, изменив своё состояние, свои настройки, прочитал у частицы этот результат В вместо результата А. Именно такое предположение выдвинул Белл, чтобы связать воедино «дополнительные переменные» Эйнштейна и статистические предсказания квантовой механики. Однако это объяснение не может быть приемлемым, поскольку нарушаются выводы другой теории – специальной теории относительности. Вариант другой. Можно предположить, что ближайший измеритель… просто выдал ложный результат, солгал! Получив результат измерения - С (вероятностное, случайное значение, никак не связанное с измерением на удалённой системе и не совпадающее с предсказанием «неполной» квантовой механики), он отбросил его и выдал нам результат В – зависимый от удалённого измерителя. И вновь это означает, что есть (сверхсветовая) передача сигнала от удалённого измерителя к близлежащему измерителю. Не трудно заметить, что оба эти варианта в определённой степени схожи. Как понимать слова Белла «влиять на чтение»? Очевидно, это не то же самое, что «влиять на состояние второй системы». Влияние на чтение означает ни что иное, как изменение состояния второго измерителя! То есть, измеритель сам что-то измерил, перешёл в соответствующее состояние, но сигнал от удалённой системы перевёл его в другое состояние, не то, которое он получил в результате собственного измерения. Если состояние второго измерителя изменилось, что можно сказать о состоянии второй, ближней системы? Только одно: оно нам не известно, поскольку о нём мы можем судить только по информации, поступившей к нам от этого второго, ближнего измерителя! То есть, по Беллу это означает использование неточного прибора, который призван устранить ошибочность исходных предположений рассматриваемой локальной теории. Приведём детали выводов Белла: 1.Запрещена связь между частицами, но она неизбежна между приборами. 2.Запрещена связь сверхсветовая, но между приборами она неизбежна. Однако «неизбежные» выводы Белла на самом деле должна означать безвыходность ситуации для «дополнительных переменных». Их наличие требует сверхсветовой передачи сигнала! Поскольку в исходной «полной» квантовой теории по Эйнштейну между частицами такая связь отсутствует, то она навязчиво выступает в таком «пародийном» виде – сверхсветовой связи между измерителями. То есть в более широком смысле можно сказать, что Белл приходит к выводу: корреляция результатов без связи между системами (частица + измеритель) невозможна и она – сверхсветовая (о том, как она достигается в «неполной», традиционной квантовой теории, умалчивается). Выводы Белла показывают, что полученный результат (корреляция) фактически полностью адекватен сверхсветовой связи между системами (частица + измеритель). Придерживаясь лоренц-инвариантности «полной» квантовой механики, Белл показывает, что «дополнительные переменные», тем не менее, нарушают её. Эйнштейн не предлагает решения проблемы, поскольку не рассматривает не - вероятностную зависимость. Однако наблюдаемое явление не может быть описано иначе, чем более сильная, нежели случайная, зависимость измерений, которая практически схожа с влиянием одного измерения на другое. Белл это доказывает в самом общем виде. Хотя доказательство Белла должно было показать отсутствие зависимости между измерениями, и в этом смысле его доводы совпадают с целями Эйнштейна (показать отсутствие связи между системами), но выводы убеждают, что измерения являются зависимыми. Белл явно не приводит эту зависимость (закон Малуса): 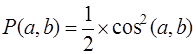 P(a,b) – вероятность совместной регистрации двух запутанных частиц; (a,b) –угол между измерителями. Можно ли, рассматривая эту зависимость, сказать иначе, нежели «результат одного измерения зависит от угла (настройки) удалённого измерителя»? Настройка удаленного измерителя явным образом влияет на результат измерения на данной системе. И Белл доказывает это вполне убедительно: результаты измерений зависят друг от друга, они не являются независимыми, вероятностными. Есть ли другое описание явления? Могут ли результаты измерений быть не случайными (по отношению друг к другу) и вместе с тем независимыми (друг от друга)? Однако нелокальность утверждает это. По Эйнштейну результаты измерения частиц косвенно являются зависимыми. Эта зависимость формируется в момент запутывания частиц и сохраняется до конца опыта. То есть, случайными состояния частиц формируются в момент их разделения. В дальнейшем они сохраняют полученные при запутывании состояния, и «хранятся» эти состояния в неких элементах физической реальности, описываемых «дополнительными параметрами». «Но одно предположение представляется мне бесспорным. Реальное положение вещей (состояние) системы S2 не зависит от того, что проделывают с пространственно отделённой от неё системой S1». [6, c.290] «…так как во время измерения эти две системы уже не взаимодействуют, то в результате каких бы то ни было операций над первой системой, во второй системе уже не может получиться никаких реальных изменений». [7] В своих выкладках Белл конкретизирует эти представления Эйнштейна в форме набора параметров, обозначив их λ. Состояния систем возникают случайно, правда, не в точке разделения систем, а в точках измерения, по «записям» в дополнительных переменных. И такая вероятностная закономерность, как доказал Белл, исключена. Но даже в этом случае результаты измерений оказываются зависимыми друг от друга. Действительно, если частицы принимают свои значения, зависимые от скрытых параметров λ – «результат А измерения σ1∙a зависит от a и λ, а результат B измерения σ2∙b в том же самом случае зависит от b и λ» [0], но и сами параметры λ были взаимосвязаны при разделении систем, то это ни что иное, как опосредованное влияние измерений друг на друга. Опосредованное, но, тем не менее, – влияние, зависимость. То есть, это влияние измерений друг на друга или влияние частиц друг на друга (против чего выступает и Эйнштейн), Белл заменяет влиянием друг на друга дополнительных параметров. Исходным предположением было отсутствие такого влияния - «дальнодействия». Но совсем отказаться от него оказалось невозможно, поэтому Белл выдвинул идею о том, что друг на друга должны влиять измерители. Либо, учитывая, что связь между частицами заменена аналогичной связью между «дополнительными параметрами», измерители влияют друг на друга и «настраивают» их. В чем различие двух механизмов влияния? Рассмотрим их подробнее. 1. Одна частица влияет на другую 2. Один измеритель влияет на другой измеритель. В первом случае измерители друг на друга не влияют и показывают истинное, правильное состояние частиц. То есть измерение истинное, приборы не лгут. Такое влияние частиц друг на друга отрицает вероятностный характер их связи и подтверждает предсказания квантовой механики, но требует а) связи, б) сверхсветовой передачи сигнала. Во втором случае, частицы ведут себя вероятностно. Но это не согласуется с предсказаниями квантовой механики (и эксперимента). В этом случае измерители выдают не вероятностные результаты (подтверждаемые экспериментом). То есть измерители показывают не то, как ведут себя частицы, которые, как мы предполагаем, ведут себя вероятностно. Следовательно, приборы – лгут! Но ведь для того, чтобы солгать нужным образом, приборы должны передать друг другу информацию. Какую? Откуда они знают, как нужно солгать? Очевидно, перед тем, как солгать, они измерили истинное, вероятностное состояние частиц. Затем, используя эти данные, исказили их таким образом, что результат оказался не-вероятностным. Но мы видим лишь показания измерителей, поэтому о вероятностном характере поведения частиц знать не можем. Кстати, для создания существующей картины, первому из измерителей искажать результат, видимо, не обязательно. Иначе, он должен будет «придумать» исход не только для второго измерителя, но и для себя самого. Хотя такая асимметрия ничем не оправдана, процедура измерения могла бы выглядеть примерно так: Частицы имеют вероятностные состояния А и В. Первый из измерителей регистрирует состояние А, но выдаёт результат D, передавая второму измерителю указание показать результат C, лишая его возможности самому исказить результат. Вот такие интриги при квантово-механическом дворе должны разыграть измерители, чтобы выполнить установку (задание, стоящее перед ними), сформулированную Беллом: - подогнать поведение частиц под вероятностный характер (сохранив согласие с экспериментом и «неполной» квантовой механикой); - исключить связь между частицами; - сохранить лоренц-инвариант системы. Вывод, приведённый Беллом, фактически подразумевает подтасовку результатов измерителями. Но и при этом мы наблюдаем всё те же – квантово-механические показания измерителей! То есть полностью согласующиеся с экспериментом. Вероятностное поведение частиц по-прежнему «скрыто» от наших глаз, и влияние измерителей друг на друга не даёт ничего нового. Этот вывод Белла оказался выше им же опровергнут. Итак, из выкладок Белла можно сделать вывод, что даже с нарушением СТО допущение о влиянии измерителей друг на друга не может выявить локального характера поведения систем, их независимого друг от друга поведения на момент измерения. То есть квантово-механическая корреляция результатов измерения запутанных частиц при отрицании такого влияния не имеет рационального объяснения. Это весьма благодатная почва для мистики и религии. Однако выше уже было отмечено, что и доводы в пользу нелокальности построены на достаточно зыбком фундаменте. Независимость систем друг от друга является предположением, которое в значительной степени (и даже главным образом) основано на стремлении остаться в рамках релятивизма. Рассмотрим эти основания. Во-первых, сверхсветовая корреляция результатов измерений не противоречит специальной теории относительность, поскольку нет передачи сигнала в релятивистском смысле. Во-вторых, не зафиксирован и даже гипотетически не описан «корреляционный сигнал», хотя есть работа, в которой утверждается, что была измерена скорость передачи подобного «сигнала» [3]. В-третьих, свойством нелокальности является очевидная зависимость результатов измерения друг от друга при отрицании такой зависимости. То есть, с точки зрения теории вероятности, результаты измерений подпадают под определение событий зависимых. Действительно, как ещё можно рассматривать результаты двух измерений, если результат первого из них достоверно, то есть с вероятностью, равной единице, предсказывает результат второго измерения? Но сторонники традиционной квантовой механики не очень убедительно отрицают эту связь. В качестве довода приводится ссылка на правила вычисления вероятностей. В квантовой механике складываются не вероятности, а амплитуды вероятностей. Однако правила вычислений вряд ли могут служить объяснением механизма возникновения такой зависимости или такой вероятности. Например, выпадение орла или решки при подбрасывании монеты в классической теории вероятности вычисляется по определенным правилам. Но по какой причине возникает такое распределение, теория вероятности не объясняет. В квантовой механике правило сложения амплитуд вероятностей (волновых функций) позволяет точно вычислить результат измерений (вероятность выпадения некоторого результата), но это правило не обязано объяснять физический механизм появления таких результатов. Это означает, что нет абсолютно никаких оснований для обвинений в адрес квантовой механики за отсутствие таких объяснений! Объяснение нелокальности и несепарабельности как физических процессов, видимо, выходит за рамки этой теории. В логике известен способ доказательства, который можно назвать «доведением до абсурда». Делается некоторое исходное предположение, утверждение. Затем логическими преобразованиями получают из него выводы, которые противоречат исходным предположениям. Считается доказанным, что исходные предположения ошибочны, опровергнуты. В статье Белла явно просматриваются основные приёмы этого метода. Но вывод из рассуждений Белла сделан с очевидным отступлением от метода. Исходными предположениями (можно сказать, от имени Эйнштейна) были следующие: 1.Признание постулата специальной теории относительности о предельности скорости передачи информации, которая не может превышать скорость света. 2.Разделённые системы не влияют друг на друга, никакие изменения в одной системе не должны оказывать влияния на другую. 3.Результат измерения на одной системе является вероятностным (независимым) по отношению к результату, полученному при измерении на другой системе. Эксперимент и квантово-механические вычисления показывают, что пункт 3 нарушается. Очевидным выводом должен быть следующий: результаты измерений на двух системах не являются вероятностными. Что является альтернативой к случайной связи величин? Видимо, зависимость одной величины от другой. Эти величины связаны причинно-следственными отношениями. Но для квантовой механики это не приемлемо, поскольку теперь оказывается нарушенным пункт 2 предположений. Что является очевидной альтернативой отсутствию влияния систем друг на друга? Очевидно, наличие такого влияния! Но тогда нарушается пункт 1, поскольку налицо явное сверхсветовое «синхронное» поведение частиц. Для «спасения» пункта 1 приводятся доводы об отсутствии сигнала как такового, сигнала в релятивистском смысле. С этим очень легко согласиться, но возникает двусмысленность. Да, релятивистский сигнал не зафиксирован и пункт 1, вроде бы спасён. Но есть «синхронность», поэтому признание релятивистского постулата в пункте 1 не является убедительным обоснованием для отсутствия влияния, то есть связи. Необходимо отказаться от пункта 1, но… вместо этого вводится нелокальность, несепарабельность с нескрываемым мистическим оттенком [4]. Это не передача релятивистского сигнала. И даже вообще не передача какого бы то ни было сигнала (то, что не обнаружено, не существует!): корреляционного, квантового, сигнала коллапса, как его ни называй. То есть вроде бы какая-то передача «синхронности» есть, но её… нет. Налицо явное стремление отрицать очевидное: две системы имеют друг с другом сверхсветовую связь. Пусть она не релятивистская и не является явным опровержением СТО (через опровержение её базового постулата о скорости света). Но формально одна из систем передаёт другой системе некоторый сигнал. Поэтому очевидно, что пункт 1 экспериментально и квантово-механическими вычислениями опровергается. То есть правильным выводом из рассуждений Белла должен быть вывод: сверхсветовая связь между системами имеется [5]. Однако Белл делает странный вывод. Он по-прежнему остаётся верен первому пункту. Это и вынуждает его сделать этот странный вывод, который иначе, как «шутливым» не назовёшь. Вместо очевидно опровергнутой предпосылки об отсутствии связи между системами, он вводит связь между… измерителями. Хотя формально это мало что меняет: сверхсветовая связь нужна, но она всё равно не позволяет выявить вероятностное поведение независимых систем. Признание сверхсветовой связи между системами должно быть признано как следствие метода «доведения до абсурда». Поскольку отказ от сверхсветовой «нерелятивистской» (?) связи между частицами приводит к неприемлемому результату, следовательно, такая связь имеет место. Однако мистическая нелокальность лучше. Но она лучше только, если не попытаться объяснить её механизм, который явно выглядит именно как сверхсветовая передача «нерелятивистского» (?) сигнала. Вопрос в скобках означает, что не исключается и материальная связь, пока не зарегистрированная, то есть некими частицами или волнами, распространяющимися с нарушением СТО. Теперь, рассматривая всё в обратном порядке, видим, что нарушение пункта 1, в свою очередь, приводит к опровержению пункта 2. Это противоречит представлениям Эйнштейна о «дальнодействии», но полностью соответствует его представлениям об элементах физической реальности. А это уже намного больше физика, чем мистика несепарабельности и нелокальности. О пункте 3 можно сказать лишь, что он как был, так и остался ошибочным предположением. Возражения Эйнштейна о полноте квантово-механического описания действительности, таким образом, приобретают новое звучание. Литература 1.Aspect А. «Bell’s theorem: the naive view of an experimentalist», 2001, (http://quantum3000.narod.ru/papers/edu/aspect_bell.zip) 2.Bell J.S., On the Einstein Podolsky Rosen paradox, Physics Vol.1, No.3, pp.198-200, 1964 3.Zbinden H., Brendel J., Gisin N., Tittel W., Experimental test of non-local quantum correlation in relativistic configurations, Group of Applied Physics, University of Geneva, February 7, 2006 (2000) 4.Доронин С.И., Сепарабельные состояния, Квантовая Магия, том 4, вып. 4, стр. 4124-4133, 2007, http://www.quantmagic.narod.ru/volumes/VOL442007/p4124.html 5.Путенихин П.В., Квантовая механика против СТО, Квантовая Магия, 4, 2130 (2007), http://quantmagic.narod.ru/volumes/VOL422007/p2130.html 6.Эйнштейн А. Собрание научных трудов в четырех томах. Том 4. Статьи, рецензии, письма. Эволюция физики. М.: Наука, 1967, http://eqworld.ipmnet.ru/ru/library/books/Einstein_t4_1967ru.djvu 7.Эйнштейн А., Подольский Б., Розен Н. Можно ли считать квантовомеханическое описание физической реальности полным? / Эйнштейн А. Собр. научных трудов, т. 3. M., Наука, 1966, с. 604-611 06.02.2008 Адрес полного текста статьи в интернете URL: http://samlib.ru/editors/p/putenihin_p_w/bell.shtml Иллюстрации и уравнения к статье (зеркала) http://samlib.ru/editors/p/putenihin_p_w/ https://cloud.mail.ru/public/8WpP/qeaUMAiGz https://cloud.mail.ru/public/Hq7e/jZ9YZGJW9 https://yadi.sk/d/EZg36rrKmJDwk https://drive.google.com/folderview?id=0B0uM56-EnG4ZaUFJb0YzY3YtcVU&usp=drive_web http://fileload.info/users/putenikhin/ | |
| Категория: Разное | | | |
| Просмотров: 3243 | Загрузок: 74 | |
| Всего комментариев: 0 | |