Путенихин П.В., Путешествие под горизонт черной дыры с возвратом
| [ Скачать с сервера (3.59 Mb) ] | 04.02.2016, 18:17 |
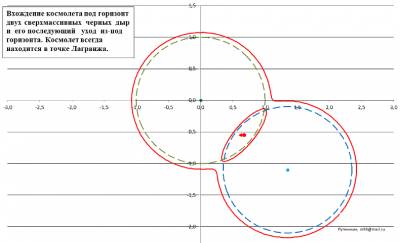
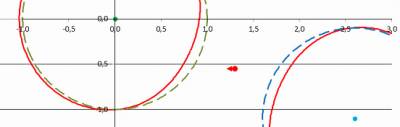
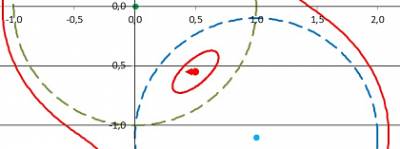
Путенихин П.В. m55@mail.ru Аннотация Известно, что попасть под горизонт черной дыры можно, но нельзя затем вернуться обратно. В предлагаемой работе рассматриваются некоторые противоречия в таких представлениях. Существует реальная физическая возможность приблизиться к черной дыре ближе, чем почти на половину её гравитационного радиуса, после чего беспрепятственно покинуть её. Статья содержит анимацию. Известно, что Черные дыры были предсказаны задолго до появления общей теории относительности как объекты, способные удержать на своей поверхности даже свет. Ничто, попав в Черную дыру, не может покинуть её: «Черной дырой называют область пространства-времени, в которой гравитационное поле настолько сильно, что не позволяет даже свету покинуть эту область и уйти в бесконечность» [1]. Однако, есть некоторые особые условия, которые я рассмотрел в моей предыдущей работе [3], при которых космический корабль может попасть, а затем беспрепятственно покинуть область под горизонтом сверхмассивной черной дыры. Действительно, можно задаться простым вопросом: какой горизонт «затащит» космолет к себе, если черные дыры находятся по обе стороны от него? В космологии известна так называемая точка Лагранжа, точка между двумя другими массивными телами, находясь в которой тело остаётся неподвижным, не падает ни на одно из этих тел: «Точки Лагранжа… точки в системе из двух массивных тел, в которых третье тело … может оставаться неподвижным относительно этих тел» [2]. Вполне очевидно, что для космолёта такими массивными телами могут быть две одинаковые черные дыры. Если дыры сблизятся настолько, что их горизонты пересекутся, как показано в работе [3], то корабль окажется одновременно под горизонтами обеих черных дыр и сможет при некоторых условиях покинуть их. Однако, результат был получен в общем виде, поскольку не учитывались ни скорость сближения дыр, ни скорость корабля. В общем случае тоннель между черными дырами закроется раньше, чем корабль сможет его пересечь. С другой стороны, в случае черных дыр, вращающихся вокруг общего центра масс, их сближение может быть сколь угодно долгим, и космический корабль заведомо сможет покинуть горизонт. При этом следует отметить, что внутреннюю область горизонта, которая образуется пересечением горизонтов двух дыр, называть горизонтом, может быть, не вполне корректно. Действительно, на анимации было четко показано, как деформируются фактические (в отсутствии поблизости других массивных тел) горизонты сближающихся черных дыр. Хотя космолёт и находится в пределах математического гравитационного радиуса каждой дыры, но напряженность гравитационного поля в этой области существенно меньше, чем под «чистым горизонтом». Тем не менее, гипотетическая возможность проникнуть под горизонт черной дыры и затем покинуть его всё-таки остаётся. Например, можно сначала переместить космолёт под горизонт черной дыры, а затем «деформировать» горизонт таким образом, что космолёт окажется вне него. По всей видимости, это возможно, поскольку время на космолёте и под горизонтом дыры для внешнего наблюдателя будет остановлено, и для «деформации» горизонта дыры у него есть неограниченное время. По часам на космолёте при этом пройдёт совсем немного времени, почти мгновение. Для указанной «деформации» горизонта необходимо, чтобы другая сверхмассивная дыра прошла «параллельным курсом» или по дуге, но касательно, с небольшим перекрытием задевая исходную черную дыру. Здесь нужно отметить очевидное общепринятое допущение, что под горизонтом черных дыр находится пустое пространство, а вся масса черной дыры сосредоточена в её центре, в сингулярности. Выведенные в упомянутой работе уравнения позволяют построить динамическую математическую модель (анимацию) процесса формирования доступных зон внутри горизонта и на достаточно близком расстоянии от центра черной дыры, её сингулярности: Рис.1 Вхождение космолета под горизонт двух сверхмассивных черных дыр и его последующий уход из под горизонта. Космолёт всегда должен находиться внутри области Лагранжа (тoннеля убегания) На рисунке штриховыми линиями изображены горизонты неподвижной черной дыры (зеленая линия) и дыры, движущейся мимо неё на расстоянии 1,1 rg (синяя линия). Для простоты принято, что вторая дыра движется по прямой линии, хотя все аналогичные расчеты будут справедливы и для движения по орбитальной траектории. Все расстояния на рисунке указаны в гравитационных радиусах rg, поэтому диаметры дыр равны 2 rg. На расстоянии 0,55 гравитационных радиуса от центра неподвижной дыры движется космолёт (красная стрелка с точкой). Красными линиями изображены окружности фантомных, как я их назвал, горизонтов черных дыр. Фантомными я назвал их по причине их не вполне ясной сущности. Вроде бы они в определённых условиях совпадают с горизонтами черных дыр rg = 2M, но в других условиях существенно от них отклоняются и даже образуют своеобразные эллипсоидальные полости. Вместе с тем, это всё-таки горизонты, то есть границы, при пересечении которой всякое тело и даже свет неизбежно упадут на сингулярность черной дыры. Алгоритм построения горизонтов основан на вычислении суммарной силы, действующей на тело со стороны двух черных дыр. Вкратце опишем его. Согласно закону Ньютона сила притяжения зависит от расстояния между телами. В процессе движения расстояние между космолётом и каждой из черных дыр непрерывно изменяется. Если обозначить как xiyi координаты корабля, как R1 и R2 расстояния от него до каждой из черных дыр и как x1y1 и x2y2 координаты их центров, соответственно, то в некоторый момент времени ti эти расстояния будут:  Массу космолёта принимаем равной единице. Следовательно, силы притяжения космолёта к двум черным дырам, каждая из которых имеет массу M, будут:  Суммарная сила определяется путём векторного сложения этих сил, поскольку они действуют не по одной линии, они не коллинеарные. В этом случае модуль суммарной силы определяется с помощью проекций частных сил на оси координат:  Главным условием образования суммарного горизонта двух черных дыр является равенство результирующей силы той силе, которая удержит космолёт от убегания на бесконечность. То есть, результирующая сила притяжения двух черных дыр на общем горизонте должна быть равна:  Это и есть условие образования суммарного горизонта. Этот суммарный горизонт двух черных дыр отличается по расположению в пространстве от их математических горизонтов, поэтому я называю его фантомным. Для космолёта не имеет значения, сколько массивных тел его притягивают. Важно, чтобы эта результирующая сила была точно такой же, как и сила на горизонте одной черной дыры с массой M. Другими словами результирующая сила в пространстве вокруг двух черных дыр образует новую поверхность сложной формы, отличающейся от обычной, сферической. Это и есть фантомный горизонт. В каждой точке этой поверхности на тело действует сила F0, не дающая ему улететь на бесконечность. Для построения этой поверхности я воспользовался методом радарного сканирования, то есть, перебором всех точек пространства вокруг дыр наподобие авиационных радаров и определения силы притяжения в них. Координаты точек, в которых обнаружена сила, равная F0, нанесены на схему рис.1. Как и ожидалось, форма фантомного горизонта имеет замысловатую форму и изменяется в зависимости от расстояния между дырами. При некоторых расстояниях между черными дырами помимо внешнего горизонта образуется ещё и внутренний горизонт - замкнутая линзообразная область. Для проверки правильности построений рассмотрены два граничных случая. Когда расстояние между дырами равно бесконечности (реально – 10 гравитационным радиусам), фантомный горизонт сливается с математическим. Это видно на первом кадре анимации. Второй случай – слияние двух дыр. В этом случае фантомный горизонт оказался равным 1,4…1,5 гравитационных радиусов, точнее, в √2 раз больше математического. Это верный результат, поскольку при увеличении массы черной дыры в два раза, её горизонт увеличивается именно √2 раз. Итак, как показано на рисунке на первом шаге эксперимента, космический корабль, космолёт, прибыл издалека и находится на достаточно безопасном расстоянии от черной дыры. В любое время он может включить свои реактивные двигатели и удалиться от неё на бесконечность. Но его задача иная, для выполнения которой он должен всегда находиться точно на середине линии, соединяющей центры черных дыр. Эта точка является точкой Лагранжа. Издалека к неподвижной черной дыре приближается движущаяся черная дыра такой же массы. Анализ движения начинаем с её удалённости на 10 rg, - это первый кадр анимации. В момент, когда дыра приблизилась до 6 rg, появляется (становится видимым) космолёт. В дальнейшем при сближении дыр космолёт корректирует своё положение в пространстве, стремясь всегда находиться в точке (области) Лагранжа: Рис.2 При сближении двух сверхмассивных черных дыр космолёт всегда должен находиться внутри области Лагранжа (вблизи тоннеля убегания) На рисунке видно, что фантомные горизонты черных дыр деформировались, «вдавились» внутрь горизонта математического. Это означает, что любое тело, оказавшись под исходным, математическим горизонтом, уже не будет затянуто черной дыры, тело сможет покинуть эту область. Новым, фактическим горизонтом становится фантомный. В случае попадания под этот горизонт ни тело, ни свет уже не смогут вырваться. При дальнейшем сближении черных дыр, деформация горизонтов усиливается и, наконец, образуется особая полость внутри горизонтов черных дыр: Рис.3 При сближении двух сверхмассивных черных дыр образуется полость внутреннего горизонта Эллипсообразная или сплюснутая сферическая полость горизонта (красный овал на рисунке) – это весьма интересное явление в «жизни» черных дыр. Эта полость – тоже пространство, ограниченное горизонтом событий, только это довольно странный горизонт. Обычные горизонты черных дыр поглощают вещество и направляют его внутрь, к своей сингулярности. Особая, фантомная полость горизонта событий между двумя черными дырами делает всё с точностью до наоборот. В центре такой полости тело не испытывает никаких усилий, это точка Лагранжа. А вот, если пересечь эту границу, то одна из черных дыр тут же захватит тело и отправит его за пределы этой полости, в свою сингулярность. Присутствие рядом двух чёрных дыр, очевидно, формирует приливные силы, значительно возрастающие от центра полости к её границе. Волосы у астронавта в центре этой полости буду стоять торчком, поскольку каждый волосок на его голове будет падать в свою близлежащую сторону горизонта полости. Поэтому наш космолёт стремится двигаться таким образом, чтобы не приближаться к границам этой полости, стараясь всегда находиться в её центре. Через некоторое время, двигаясь, полость повернётся вокруг центра неподвижной черной дыры и окажется на противоположной стороне по ходу движения: Рис.4 Через некоторое время движения двух сверхмассивных черных дыр полость внутреннего горизонта перемещается на другую сторону Космолёт вместе с полостью переместился на другой край неподвижной черной дыры. Процесс зеркальным образом повторяет то, что было вначале. Поэтому не является неожиданным раскрытие полости и образование тоннеля убегания, то есть, своеобразного коридора, через который космолёт может уйти, убежать от воздействия сил притяжения черных дыр. Теперь уже ничто не мешает космолёту покинуть промежуточное пространство между дырами: 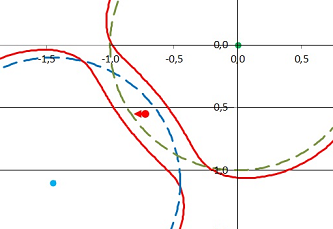 Рис.5 Две сверхмассивные черные дыры разошлись и образовали тоннель убегания То, что космолёт всё ещё находится внутри математических горизонтов обеих черных дыр, ничего не значит. Это всего лишь пустое пространство, в котором каждая из черных дыр, будучи одинокой, захватила бы космолёт. Но здесь этому мешает её напарница. Вдвоём они «тянут» космолёт в разные стороны, давая ему право самому решать, используя свои двигатели, куда двигаться. Реально действующие, фактические горизонты дыр, имеющие название фантомных, теперь уже находятся далеко и не могут помешать космолёту свободно удалиться. Ему нужно лишь одно: покинуть область математических горизонтов черных дыр, очерченную штриховыми линиями, до того, как дыры разойдутся достаточно далеко. Итак, мы видели картину, как космолёт приблизился к центрам чёрных дыр на расстояние почти в половину их гравитационных радиусов. Как это возможно? Ведь теория относительности не допускает возможности пересечения горизонта изнутри, а тело, попавшее под него, с неизбежностью упадёт на сингулярность. Здесь, в описанном мысленном эксперименте такого падения не происходит! То, что истинные горизонты двух черных дыр никуда не исчезли, можно увидеть, если предположить, что они сблизятся на расстояние, меньшее гравитационного радиуса. В этом случае они окажутся под гравитационными радиусами друг друга и, вне всяких сомнений, сольются в одну. Внутренняя область на таком расстоянии уменьшается до нуля. Конечно, можно утверждать, что расчеты содержат ошибки. Но это не имеет особого смысла и легко проверяется. Сама же логика эксперимента говорит: всё должно происходить так, как описано. И, как это часто бывает, этот эксперимент не столько даёт ответы, сколько ставит новые вопросы. Первое, что, вполне возможно, может сразу прийти в голову: а, может быть, теория относительности неверна? Ну, это плохой вопрос, мало что проясняющий. Действительно, некоторые ведущие космологи допускают, что сингулярность – это свидетельство ошибочности теории или, по крайней мере, свидетельство её неполноты. Но эту тему здесь обсуждать мы не будем. Было бы лучше выполнить все расчеты по данному эксперименту более полно, в рамках общей теории относительности. Вполне возможно, что решение окажется иным и космолёту не выжить внутри горизонтов. Хотя такой исход крайне маловероятен. Пришлось бы отправить в утиль и некоторые ныне вполне дееспособные физические законы, лишь бы получить релятивистское опровержение этого эксперимента. Но, если этот мысленный эксперимент справедлив, тогда возникают другие вопросы. При коллапсе звезды в черную дыру, согласно общей теории относительности, время на её горизонте замедляется настолько, что для внешнего наблюдателя движение полностью прекращается. Это означает, что вещество звезды с его точки зрения практически никогда не достигнет сингулярности и даже самой поверхности горизонта. Другими словами, для внешнего наблюдателя сингулярности не существует. Всё вещество звезды, её поверхность останутся на своих местах, тех местах, где их видели в последний раз. То есть, условно говоря, пространство под горизонтом черной дыры – это не есть пустое, эфемерное, хотя и гравитирующее пространство. Это вполне твёрдая, из спрессованных нейтронов поверхность, сквозь которую не провалишься – хоть на танке проезжай. А танк будет весить многие миллионы тонн! И при этом наш космолёт свободно прошёл сквозь эту «нейтроно-бетонную» стену! Так прошёл или же всмятку? Вот это уже интересный вопрос. Считается, что астронавт, падающий в сверхмассивную черную дыру, не испытает никаких воздействий. Он даже не заметит момента, когда пересечёт горизонт. Только позади него, как говорится, ему увидится «небо в копеечку», копеечку, пылающую как множество Солнц. Это вполне вероятно, поскольку за время его падения на сингулярность снаружи пройдёт вечность, и весь свет, падающий на черную дыру с его стороны, превратится в один мощнейший поток фотонов, копившихся вечность, но прилетевших в один момент. Вторая черная дыра из нашего эксперимента, пролетевшая мимо и лишь частично коснувшаяся горизонта, также пролетит мимо него за один краткий миг. И полость фантомного горизонта – тоже. Что произойдёт в этом случае? В полости время течёт как снаружи, ведь в ней нет такого сильного искривления пространства-времени. Коснувшись этой полости, оказавшись в ней, свободно падающий астронавт окажется вдруг во времени внешнего наблюдателя. И все скорости движения и темп времени у него станут такими же. А это, видимо означает одно: спасение. Ему только-то и нужно, что попасть в дрейфующий с полостью космолёт. Всё это произойдёт спустя мгновение после перехода астронавта под горизонт черной дыры. Более того, он даже и не заметит, что был в остановленном времени. При этом у внешних наблюдателей для такого спасения есть тысячи и миллионы лет. Здесь явно видна машина времени. Но только для астронавта и только для движения в будущее. В точке максимального сближения двух черных дыр величина приливных сил достигнет наибольшего градиента. При малейшем отклонении от центра фантомной полости они будут возрастать вплоть до величины на горизонте. Выдержит ли астронавт и космолёт эти силы? Каковы должны быть размеры сверхмассивных черных дыр и величина перекрытия их гравитационных радиусов, чтобы космолёт разумных размеров не был разорван внутренними приливными силами? И, наконец, вопрос о составе вещества вблизи горизонта, под ним. Он остался без ответа. Можно предположить, что в области перекрытия горизонтов при встрече с фантомной полостью вещество мгновенно упадёт в центры черных дыр, на их сингулярности. То есть, фантомный горизонт как бы «утрамбует» нейтроны там, где пройдёт. Пока это неясно. Литература 1. Новиков И.Д., Фролов В.П., Физика черных дыр. – М. : Наука., Гл. ред. физ.-мат. лит., 1986, 328 с. 2. Википедия. Точки Лагранжа, URL: https://ru.wikipedia.org/wiki/Точки_Лагранжа 3. Путенихин П.В., Как убежать из-под горизонта черной дыры, 2015 [расчеты показывают, что есть несколько странное решение задачи, из которого следует вывод о возможности выйти из-под горизонта черной дыры], URL: http://samlib.ru/p/putenihin_p_w/escape.shtml 26.04.2015 Адрес полного текста статьи в интернете URL: http://samlib.ru/p/putenihin_p_w/tonnel.shtml Иллюстрации и уравнения к статье (зеркала) http://samlib.ru/p/putenihin_p_w/ https://cloud.mail.ru/public/8WpP/qeaUMAiGz https://cloud.mail.ru/public/Hq7e/jZ9YZGJW9 https://yadi.sk/d/EZg36rrKmJDwk https://drive.google.com/folderview?id=0B0uM56-EnG4ZaUFJb0YzY3YtcVU&usp=drive_web http://fileload.info/users/putenikhin/ | |
| Категория: Разное | | | |
| Просмотров: 3238 | Загрузок: 77 | |
| Всего комментариев: 0 | |