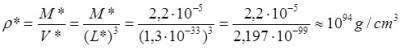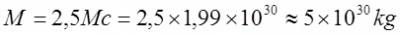Нужна ли сингулярность Черной дыре и общей теории относительности? (начало) - Разное - Публикации - Каталог научных статей

Нужна ли сингулярность Черной дыре и общей теории относительности? (начало)

[ Скачать с сервера (834.0 Kb) · Скриншот ]	28.01.2016, 18:55
Нужна ли сингулярность Черной дыре и общей теории относительности? Путенихин П.В. m55@mail.ru Аннотация Предсказание сингулярности обнаружило в общей теории относительности существенные проблемы. Ставится вопрос о неполноте теории или даже о её ошибочности. Насколько сингулярность реалистичное явление? Показано, что черные дыры могут быть описаны без привлечения понятия сингулярности как точки с бесконечно малым радиусом и с бесконечно большой плотностью. Содержание Сингулярная неполнота общей теории относительности Как в общей теории относительности возникает сингулярность Гипотеза о вырожденном фермионном газе Процессы, происходящие сразу после коллапса Как выглядит рождение черной дыры на анимации Литература Несомненно, Солнце сделано из чистого золота, именно поэтому оно так блестит. Сингулярная неполнота общей теории относительности Едва ли не в самой большей мере свою популярность теория относительности получила благодаря предсказанию сингулярностей. Сингулярность является одним из самых удивительных и загадочных физических объектов, хотя их реальное существование до сих пор ставится под сомнение. Достаточно сказать, что с нею связано само происхождение нашей Вселенной, всего Бытия, в том числе возникновение пространства и времени. «Сингулярность» переводится как «единственный, особенный» и в физике обозначает особенные состояния пространства-времени. Считается, что в так называемых черных дырах имеется гравитационная сингулярность: «Гравитационная сингулярность – область пространства-времени, через которую невозможно гладко продолжить входящую в неё геодезическую линию. … либо метрика обладает иными патологическими свойствами, не допускающими физической интерпретации» [33]. Самой первой сингулярностью следует считать космологическую сингулярность – состояние Вселенной в начальный момент Большого взрыва, характеризующееся бесконечной плотностью и температурой вещества. Космологическая сингулярность по описаниям в физической и философской литературе даёт основания присвоить ей ещё и «титул» - «божественная сущность». Действительно, обычное описание Большого взрыва можно сформулировать кратко, что Вселенная возникла «Нигде, Никогда, из Ничего». Тем не менее, такое иррациональное происхождение вопреки даже мнению его сторонников в современной физике всё-таки сводится к наличию чего-то «до сингулярного». Это либо некие инфлатонные поля, либо скалярные поля иного содержания, либо пульсирующие Вселенные, то возникающие из сингулярности, то вновь в них проваливающиеся. Не менее загадочно обстоят дела и с гравитационной сингулярностью. «Гравитацио́нная сингуля́рность … - точка (или подмножество) в пространстве-времени, через которую невозможно гладко продолжить входящую в неё геодезическую линию. В таких областях становится неприменимым базовое приближение большинства физических теорий» [7]. Наблюдать сингулярности непосредственно невозможно, при нынешнем уровне развития физики они являются лишь теоретическим построением. Считается, что описание пространства-времени вблизи сингулярности может дать квантовая гравитация. Такие сингулярности менее фундаментальны, чем космологическая, и считается, что они присущи конкретным объектам во Вселенной – черным дырам. В отношении таких сингулярностей ведущие физики довольно определённо признают нефизичность этого понятия: «Строго говоря, появление сингулярностей в теории сигнализирует о том, что эта теория является неточной или неполной. Поэтому уже сам факт существования сингулярностей бросает вызов теоретикам» [36]. Речь идёт, конечно же, в первую очередь об общей теории относительности, которая математически предсказывает существование черных дыр и сингулярностей в них. Английский физик Стивен Хокинг определяет сингулярность как «место, где разрушается классическая концепция пространства и времени так же, как и все известные законы физики» [40]. Получается, что Хокинг практически признаёт, что современная физики пока не может ни описать, ни объяснить строение чёрной дыры. «существует ли «космический цензор», запрещающий появление голых сингулярностей и облачающий каждую из них в абсолютный горизонт событий?» [21]. Этот вопрос является, возможно, самым фундаментальным нерешенным вопросом общерелятивистской теории коллапса. По очевидным соображениям «увидеть» сингулярность в прямом смысле невозможно – в этом отношении нет особой разницы между горизонтом событий черной дыры и «чистой» сингулярностью. В цитате отражается факт того, что гравитационные сингулярности могут возникать только внутри черной дыры, и какова причина этого, какой «космический цензор» установил это правило, неизвестно. Проблему невозможности описания сингулярности в общей теории относительности в настоящий момент решить не удаётся, но есть надежда, что в будущем, пока ещё только развивающаяся: «квантовая гравитация действительно устранит сингулярности» [21]. Хотя, как видим, здесь речь идёт не столько об описании самой сингулярности, сколько, как можно понять, о замене её на более физичную сущность. Сама сингулярность как бесконечно малая область с бесконечно большой плотностью должна уйти из теорий. Тем не менее, неясно, чем её можно будет заменить, поскольку черные дыры уже фактически обнаружены, описать их поведение без гравитационной сингулярности практически невозможно. Возникновение черных дыр и сингулярностей в них связывают исключительно с последним этапом в жизни звёзд – коллапсом. Коллапс… «…по крайней мере в рамках общей теории относительности … неизбежно приводит к возникновению сингулярности» [21]. Инварианты, характеризующие кривизну пространства-времени, в процессе коллапса неограниченно возрастают, и через конечное время по часам на коллапсирующем теле кривизна в его центре становится бесконечно большой. Тело непрерывно сжимается и его плотность неограниченно возрастает: «При этих условиях естественно ожидать возникновения сингулярности или какой-либо иной «неприятности» [21]. И действительно, сингулярность для общей теории относительности и для физики в целом является серьёзной неприятностью. Нет не только более или менее приемлемой теории явления, но оно самим фактом своего существования противоречит всем известным законам физики. То есть, любая существующая или новая теория, которая должна описывать сингулярность, уже изначально будет им противоречить. Сжатое до бесконечной плотности вещество находится в том особом состоянии, которое теоретики описывают как сжатое в пространстве и застывшее во времени. «По сути своей, этот загадочный регион больше не подчиняется главным законам вселенной» [8]. Парадоксально, сингулярности не подчиняются известным законам физики, но при этом являются неизбежным следствием математического формализма общей теории относительности, её прямым следствием: «Что сингулярности представляют собой весьма общее явление и что при всем желании от них невозможно избавиться, было известно уже начиная с 1965г. благодаря теоремам о сингулярностях» [15]. И это предсказание, не имеющее до сих пор наблюдательного опровержения, оказывает на теорию, так сказать, обратное воздействие, ставя под сомнение истинность теории, которая сама же их и предсказала. В связи с нежелательностью предсказываемых уравнениями Эйнштейна сингулярностей высказывались мнения, что это служит «убедительной причиной для модификации этих уравнений» [15]. В физике возник кризис в связи предсказанием теорией относительности Эйнштейна неизбежности существования сингулярностей. В сингулярной точке уравнения общей теории относительности, связывающие искривление пространства времени с распределением массы и энергии, теряют смысл. «Это означает, что общая теория относительности не может предсказать, что получается из сингулярности. … Таким образом, общая теория относительности — не завершенная теория» [38]. Согласно теории Большого Взрыва в момент своего возникновения Вселенная имела так называемую планковскую плотность – порядка 10⁹⁴ г/см³. Откуда берутся такие величины? В физике широко применяются несколько подобных величин, имеющих общее название планковских. Что будет с черной дырой при таком сжатии, неизвестно. Есть предположение, что сжатие будет происходить не до сингулярности, а до достижения плотности Планка, после чего этого снова начнется расширение. «что происходит при такой плотности, ученые предсказать не могут, но полагают, что это максимально возможная плотность вещества» [23]. Все эти «планковские» величины ведут свою историю, видимо, от академика М.А.Маркова, который предложил считать: «предельным значением величину размерности массы, которую можно скомбинировать из трех фундаментальных физических констант – постоянной Планка h, скорости света C и гравитационной постоянной G» [14]. Из этих же констант можно сконструировать величину с размерностью длины - 10^–33 см и времени - 10^–43 сек: Отсюда и появляется та чудовищная плотность первичной Вселенной. Действительно, планковская плотность равна: Правда, возникает легкое недоразумение, поскольку в этом случае масса Вселенной в стадии сингулярности довольно мала – планковская, меньше миллиграмма – 2,2х10^-5г. Это заметно отличается от предсказаний инфляционной теории Большого Взрыва. Считается, что это минимально возможные значения соответствующих величин для времени и расстояний и максимально возможное (для массы элементарных частиц) – для массы. Но почему это так? Все эти величины являются всего лишь искусными, искусственными комбинациями известных физических констант. Каким образом из этого может следовать их предельность? Что препятствует существованию в природе интервалов, меньших, чем планковская длина или время? Скорее всего, это связано с молчаливым согласием физиков, поскольку эти величины имеют довольно «красивое» происхождение, а это ведь неспроста! Значит, следует считать их граничными величинами. Однако, вряд ли такое объяснение можно считать веским обоснованием. Такие определения не сильно отличаются от шутливых, юмористических. Например, в журнале «Квант» однажды была опубликована студенческая шутка. На вопрос, что такое «нечистая сила», студенты ответили: это произведение нечистой массы на нечистое ускорение. Или похожая шутка. На КВН (игра Клуба Весёлых и Находчивых) участникам предложили придумать новую единицу измерения. И студенты быстро её придумали – один кэйф. Возникла она из выражения «быть под кайфом», то есть быть навеселе, пьяным. Один кэйф – это один грамм на градус (1 гград). Градусы, понятное дело, не температурные, а спиртовые. Сто граммов 40-градусной водки, следовательно, содержат 4 килокэйфа. Как видим, можно легко и просто придумать какое угодно «физическое» определение. Может быть, и сингулярность из их числа. Насколько обосновано введение такого понятия? Как в общей теории относительности возникает сингулярность* Математические определения сингулярности в физической литературе встречаются достаточно часто. Но крайне сложно найти объяснение её физической сущности. Например, тело массой М мы можем потрогать, померить и придумать объяснения, почему оно не проваливается сквозь землю. С сингулярностью несколько иначе: «Независимо от жесткости вещества коллапсирующей (сферической) звезды, если ее поверхность сколлапсировала под гравитационный радиус, то после этого звезда будет продолжать коллапсировать до тех пор, пока ее поверхность не будет сжата в сингулярность при r = 0» [15]. В этом описании пока не видно, в чем же состоит физическая сущность сингулярности. Если нечто стремится к нулю, это привычно. Но нулевой объём более похож на полное отсутствие чего-либо. «Мы приходим к этому выводу, вспоминая, что поверхность звезды не может двигаться быстрее света и, следовательно, угол между мировой линией поверхности и осью и на диаграмме Крускала — Шекереса должен быть всегда меньше 45^°» [15]. Диаграммы эти – вещь очень интересная и наглядная. Только и на них причина и следствие в данном случае видятся не на своих местах. Мировая линия продолжена до сингулярности. И вновь здесь мы видим только поведение сингулярности и тел, движущихся к ней. Но, что она собой представляет, в этом выводе не просматривается. «Но глубоко внутри, под гравитационным радиусом, наблюдатель встретит бесконечные приливные силы… Чтобы убедиться в этом, необходимо вычислить… «инвариант кривизны»… R имеет одну или несколько компонент, которые обращаются в бесконечность при r -> 0; это и означает, что приливные силы становятся бесконечными» [15]. Это уже некоторое, хотя и довольно абстрактное описание. Тем не менее, и в нём не видно, откуда берётся такое физическое свойство «иметь нулевой объём». Эта особенность инварианта пока выглядит как постулятивно заложенная в теорию, поэтому его поведение очевидно и никакого другого результата ждать не приходится. Если в той же ньютоновой физике мы сблизим два тела до нуля, то получим такую же бесконечную силу притяжения. Только в ней мы не отвлекаемся от физических размеров тел и не допускаем их бесконечного сближения. В теории относительности пока есть ощущение, что уравнения никак не учитывают внутреннее физическое, материальное строение вещества. «Типичные радиальные геодезические геометрии Шварцшильда, изображенные (схематически) в шварцшильдовских координатах… времениподобная геодезическая пробной частицы, которая начинает свое движение из состояния покоя … и падает прямо внутрь, достигая за конечное собственное время сингулярности r = 0 (кривая с зубцами)» [15]. 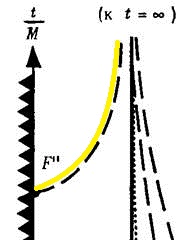Рис.1 Фрагмент рисунка ФИГ.31.1 из работы [15]. Иллюстрация того, что пробное тело обязательно упадёт на сингулярность. На приведённом фрагменте рисунка желтой линией отмечена геодезическая тела, падающего на сингулярность. Здесь это отмечается как факт. Есть траектория и считается, что она определённо будет проложена до нулевой точки. Никаких иных доводов по поводу падения на сингулярность, естественно, не указывается и на диаграмме Крускала-Шекереса: 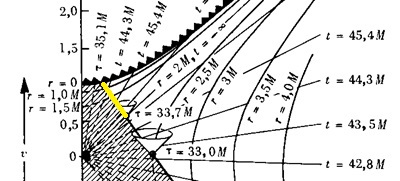Рис.2 Фрагмент рисунка ФИГ.32.1 из работы [15] Иллюстрация того, что пробное тело обязательно упадёт на сингулярность. Здесь также желтым отрезком выделен участок геодезической, отражающий падение пробного тела на нулевую точку, в сингулярность. В описаниях к диаграммам приводятся соответствующие уравнения движения, но никогда не указывается, почему пробное тело или поверхность звезды так безропотно уплотняется до бесконечности. Действительно, математика там весьма сложна. Самым простым для рассмотрения случаем обычно указывается «звезда» с однородной плотностью и равным нулю давлением. Вот это указание на нулевое давление – уже может считаться обоснованием. Однако, это давление никогда не соотносится с молекулярной твердостью этой пыли. Просто делается рекурсивная отсылка на диаграмму: вот так выглядит геодезическая. «если звезда сжалась под свой гравитационный радиус … то никакое внутреннее давление, каким бы сильным оно ни было, не может воспрепятствовать сжатию поверхности звезды в сингулярность» [15]. Ссылка на давление приводится во многих описаниях. Обычно говорится о давлении газо-пылевой среды. А ведь на пути к нулевой точке есть ещё и молекулярная (атомарная, кварковая) структура вещества. Почему силы сжатия этих структур, которые, очевидно, на много порядков сильнее гравитации, не останавливают движение к сингулярности? «С точки зрения наблюдателя внутри звезды за короткий промежуток собственного времени … после прохождения через горизонт достигается сингулярность (нулевой радиус, бесконечная плотность, бесконечные гравитационные приливные силы)» [15]. Следует заметить, что поведение давления при сжатии вещества выделено в самостоятельные разделы и при описании коллапса упоминаются лишь вскользь. А здесь у всех авторов почти негласный сговор, как заклинание – достигается. И лишь иногда проскальзывает небольшое сомнение: «можно с уверенностью говорить о наличии в конце коллапса сингулярности. Но никто не знает, какая доля вещества коллапсирующей звезды и ее физических полей пройдет через эту сингулярность — все, часть или ничего» [15]. В многочисленных описаниях коллапса, образования черной дыры трудно найти обоснования, почему нулевой объём, почему бесконечности. Представляющееся удовлетворительным определение самой сингулярности является лишь поверхностным, внешним описанием. Все геодезические (даже пути тахионов, что довольно странно) обрываются в некоторой точке и продлить её нельзя. Например, по причине бесконечной кривизны. Это, собственно, и есть сингулярность. Откуда берётся не математическая, а физическая бесконечная кривизна, мы догадываемся. Опять всё те же бесконечности и нулевые объёмы. Но откуда такая уверенность, что они, эти нулевые объёмы действительно достижимы? Теоремы Хокинга, Пенроуза о сингулярностях также опираются на эти бесконечности и фатальные обрывы геодезических по причинам, не менее загадочным, чем бесконечная кривизна. Но в теоремах тоже не указывается, каким образом реальные физические объекты позволяют тензорам и горизонтам сжимать их в бесконечно малый объём. Согласно вычислениям, слишком массивное ядро звезды будет коллапсировать, сжиматься, пока не достигнет сингулярности с нулевым радиусом. Если проследить за поверхностью звезды внутри области r = 2m, то есть под горизонтом черной дыры, то мы увидим, что она с неизбежностью достигает r = 0. Почему? Да потому, что поверхность звезды должна непрерывно двигаться во времениподобном направлении, а световые конуса наклоняются все больше и больше в сторону оси r = 0. И подтверждают всё это опять же «скаляры кривизны, построенные из тензора Вейля». А раз они стремятся к бесконечности, то наблюдатель, падающий на сингулярность, будет сжат в точку. Но даже и при этом, бесконечная кривизна вызывает у авторов меньше возражений, чем обрыв мировых линий. Хотя это, несомненно, взаимосвязано. Что, как не горизонт делает недоступной область сингулярности, фактически обрывая мировые линии, ушедших под него тел. Но какова физическая причина, сущность сингулярности? Гипотеза о вырожденном фермионном газе В литературе уже давно существует традиция. Принято приписывать приоритет последних достижений науки и техники мыслителям «давних лет», а то и вообще - древности. Например, можно встретить высказывания, что первый компьютер появился в каменном веке. В некоторых древних текстах находят «упоминания» о некоторых открытиях нынешних дней. Пожалуй, самым ярким примером являются предсказания Николы Тесла. Продолжим и мы эту традицию. В рассматриваемом вопросе возникла довольно любопытная ситуация. Теория предсказывает в строгом соответствии со своими правилами, формализмом некоторое явление. И это явление вступает в противоречие с этой самой теорией. Как такое может быть? Проблема трактовок? Прямое, буквальное продолжение выводов теории за пределы области её применимости? Как не вспомнить в этой связи строки из Пушкина: «Родила царица в ночь Не то сына, не то дочь; Не мышонка, не лягушку, А неведому зверюшку» [31] Общая теория относительности с полным правом может считаться царицей современной науки. И сингулярность, несомненно, её порождение. Вот и выходит, что задолго до Эйнштейна эту «неведому зверушку» предсказал великий русский поэт Пушкин. В физике есть немало неточных определений, которые, тем не менее, прекрасно работают. Например, до сих пор в электротехнике за направление электрического тока в металлах принимается движение положительно заряженных частиц. И всё это позволяет получить безупречные и точные результаты. Хуже дела обстоят при расширении теории за границы её применимости. В теории относительности это уже стало правилом. Например, специальная теория относительности расширена на сверхсветовые сигналы, на тахионы. В результате приходится замалчивать, закрывать глаза на возникающие при этом проблемы с причинностью, лишь бы плодить красивые уравнения и всё новые и новые мнимости. Уж очень всё это напоминает великую схоластическую задачу: сколько ангелов поместится на кончике иглы? Сингулярность в этом отношении выглядит как близкий родственник таких «заграничных вылазок». Точно так же она имеет признаки мнимостей, пустого, иррационального понятия, не дающего разумного физического воплощения. Впрочем, мнимые величины и сами по себе производят впечатление великого лукавства. В той же электротехнике, в области переменных токов мнимые величины применяются очень широко и весьма успешно, упрощая многие расчеты. В квантовой информатике мнимые величины – эффективный инструмент. Но, если внимательно приглядеться к сущности таких мнимых параметров, они оказываются самыми, что ни на есть реальными! Не нужно обладать никаким выдающимся воображением, чтобы «повесить» мнимую величину на ортогональную ось. От мнимости осталось одно лишь название. Ось вполне реальна. Таким образом, само по себе использование сингулярности как элемента математических вычислений, по сути, не должна приводить ни к каким парадоксам. Это, несомненно, удобное понятие. Но реального физического воплощения она иметь не обязана. Как «положительный электроток в металлах», мнимые составляющие мощности или мнимая масса, мнимое время. Не надо только материализовать эти математические абстракции, но никак не физические объекты. И черной дыре и общей теории относительности сингулярность, если и нужна, но лишь, пожалуй, как вспомогательный параметр, условное обозначение некоего явления. В самом деле, о сингулярности только-то и известно, что это бесконечно малая по (планковским?) размерам точка, имеющая бесконечно большую (планковскую?) плотность материи в ней, которая обрывает мировые линии. Пожалуй, единственным её выдающимся и реально наблюдаемым свойством является горизонт событий, затягивающий в себя всё, что его коснётся. По сути, в этом же состоит, видимо, и основная причина возникновения противоречий, проблем в общей теории относительности. Одним из основных признаков сингулярности пространство-время является наличие в нём неполных времениподобных или нулевых геодезических, и само оно при этом не может быть вложено в большее пространство-время. Предсказание сингулярностей означает неполноту классической общей теории относительности. «Поскольку сингулярные точки должны быть вырезаны из пространственно-временного многообразия, в них нельзя определить уравнение поля и тем самым предсказать, что произойдет с сингулярностями» [37]. Другими словами, обрывающиеся на сингулярностях геодезические означают своеобразный «конец света», этакий апокалипсис внутри каждой черной дыры. Надо, конечно, отметить, что отчасти эта проблема получила некоторое обнадёживающее продолжение с предсказанием излучения из черной дыры. Это было первым нетривиальным результатом от сочетания общей теории Эйнштейна с принципом квантования. Этот результат показал, что: «гравитационный коллапс не такой уж тупик, как казалось раньше. Частицы в черной дыре не обязаны заканчивать свою историю в сингулярности. Вместо этого они могут вырваться из черной дыры и продолжить свою историю снаружи» [38]. Конечно, по поводу «вырваться из черной дыры» Хокинг несколько преувеличил. Тем не менее, современные представления о сингулярности крайне неопределённые. Даже сам факт предсказания возникновения сингулярностей в общей теории относительности крайне смутно описывается в научной литературе. Возникновение горизонта событий не очень-то связано с последующим «схлопыванием» вещества звезды при коллапсе в точку с нулевыми размерами и бесконечно большой плотностью, которое выглядит скорее как простая логическая экстраполяция движения. Во всяком случае, все популярные учебники физики подробно описывают падение в черную дыру, но, если и упоминают, то крайне скудно причины неудержимого движения вещества в точку сингулярности. А это довольно очевидный вопрос. Например, при рассмотрении законов Ньютона такая экстраполяция пресекается «на корню». Действительно, два тела притягиваются друг к другу с силой, обратно пропорциональной квадрату расстояния между центрами тел. Казалось бы, что мешает заявить: при нулевом расстоянии тела притягиваются с бесконечно большой силой! Чем тебе не сингулярность по Ньютону? Однако, любой физик сразу же возразит: до нуля дело не дойдёт, поскольку тела задолго до этого упрутся друг в друга своими поверхностями. Вообще-то, это должно быть хорошей идеей, правильно и вовремя учесть сменившийся характер взаимодействия. Почему бы тогда при уходе поверхности коллапсирующей звезды под горизонт ей не остановится где-то посередине пути из-за того, что элементарные частицы «упрутся» друг в друга? Твердые ньютоновы тела состоят из тех же самых элементарных протонов и нейтронов, что и нейтронная звезда. Конечно, для обычных маломассивных тел сила притяжения недостаточна, чтобы преодолеть силы отталкивания молекул и атомов друг от друга. Но откуда взялась эта идея, что при чрезмерно большой силе сдавливания нейтроны сожмутся до размеров, меньше кварков и ещё намного сильнее? Есть такое образное сравнение: «Нейтронная звезда – это своеобразное атомное ядро поперечником в десяток километров. В такой звезде ядерные частицы – нуклоны – очень тесно прижаты друг к другу» [19]. Такие плотно прижавшиеся друг к другу нуклоны – нейтроны – называют нейтронным газом. Если масса такой нейтронной звезды не превосходит примерно две массы Солнца, то нейтронный газ способен квантовыми силами воспрепятствовать дальнейшему сжатию звезды. Однако, сравнение с атомным ядром - это всего лишь образное сравнение. На самом деле это всё-таки разные объекты: «нейтронные звезды и ядра атомов – совершенно разные физические объекты. В частности, в ядрах нуклоны притягиваются с помощью «сильного взаимодействия», а в нейтронной звезде – «силой гравитации» [18]. Но может ли гравитация сжать нейтроны в ядро меньшего диаметра, чем ядерные силы сильного взаимодействия, которые по силе превосходят гравитацию в 10³⁸ раз? Возникает крамольный вопрос: а, может быть, сингулярности-то и нет? Может быть, при уходе нейтронной звезды под горизонт, она под действием ядерных сил просто образует новый, специфический элемент периодической системы Менделеева? С громадным атомным (порядковым) номером. Практически у всех авторов описание возникновения сингулярности в результате коллапса нейтронной звезды совпадают по основным признакам. Одно из наглядных описаний приводит Новиков: «Чтобы избавиться от эффектов, не имеющих непосредственного отношения к образованию черной дыры и только осложняющих решение, рассмотрим сжатие сферического облака вещества, лишенного давления, р = 0 (облако пыли)» [21]. Но возникновение сингулярности при таких условиях совершенно естественный процесс. Что может помешать пыли собраться в ничтожно малый комок? Частички её имеют, как считается, нулевой объём, а суммарный объём конечного числа частиц с нулевым объёмом, разумеется, равен нулю. Кроме того, как указано, это облако пыли не оказывает никакого сопротивления сдавливанию. Впрочем, далее есть пояснение: «сделанное выше предположение об отсутствии давления ничего качественно не меняет в картине образования сферической черной дыры. В общем случае сжатия шара с давлением (р ≠ 0) картина такая же. Когда поверхность сжимающегося шара приближается к сфере Шварцшильда, никакое давление не может предотвратить возникновение черной дыры» [21]. Казалось бы, возникло противоречие. Но это не так. Строгие математические выкладки многих авторов подтверждают, что никакое давление не способно удержать вещество от падения на сингулярность. Хотя это и несколько странно. Получается, что сжимать упругую среду можно до сколь угодно малых размеров. Для этого, по меньшей мере, давление при сжатии не должно неограниченно возрастать. Литературный обзор описаний процесса возникновения сингулярности показал, что в русскоязычной литературе по космологии почти все ссылки прямо или косвенно указывают на один и тот же источник. Это учебное пособие для вузов в 10 томах Л.Д.Ландау и Е.М.Лифшица [11, 12, 13]. Главной, если не единственной причиной возникновения сингулярности в момент коллапса указывается переход нейтронов, образующих нейтронную звезду, в состояние вырожденного фермионного газа: «Совокупность нейтронов, из которых состоит звезда, можно считать вырожденным фермионным газом… Таким образом, если нейтронная звезда имеет массу, большую, чем масса солнца, то составляющие её нейтроны должны рассматриваться как вырожденный релятивистский ферми-газ» [3]. Вырожденный фермионный газ – это такой газ, на свойства которого оказывают существенное влияние квантово-механические эффекты. Вырожденный фермионный газ – ферми-газ – образуется фермионами, к которым относятся и нейтроны. При некоторых условиях в него и вырождается, то есть, превращается указанный выше нейтронный газ звезды: «Вырождение наступает в условиях, когда расстояния между частицами газа становятся соизмеримыми с длиной волны де Бройля» [4]. Очевидно, что нейтроны при сильном сжатии уже будучи в состоянии нейтронной звезды находятся на столь близком расстоянии, что такое приближение становится очевидным: «при достаточном сжатии вещества роль взаимодействия электронов с ядрами (и друг с другом) становится несущественной, так что можно пользоваться формулами идеального ферми-газа... при достаточно большой полной массе М тела можно рассматривать вещество тела как вырожденный электронный ферми-газ…» [13]. Считается, что для всякого вещества существует предельное давление, которое оно может оказать при сжатии. Со ссылкой на том 2 «Теорию поля» Ландау и Лившица уравнение для такого предельного давления приводит Садовский, отмечая, что: «следующее отсюда давление является предельным давлением, которое может иметь какое-либо макроскопическое тело» [32]. Для определённости в терминологии примем следующие определения невырожденных газов, которые обычно называют также идеальными газами, и вырожденных газов, к которым относятся и рассматриваемые нами ферми-газы: «Газы, подчиняющиеся законам классической механики, будем называть невырожденными. Для таких систем частиц применяется классическое распределение Максвелла-Больцмана. Газы, починяющиеся квантовым статистикам, называют вырожденными» [22]. Для нас особо важным и интересным является характерная особенность вырожденного газа – зависимость его давления практически только от плотности: «Характерное свойство вырожденного газа - зависимость давления только от плотности и крайне слабая зависимость от температуры» [24]. Такое состояние вырожденности газа возникает, в частности, когда плотность достаточно велика, так что соседние частицы начинают «чувствовать» друг друга. На это обстоятельство следует обратить особое внимание. Утверждается, что плотность фактически зависит только от объема газа, поскольку принято, что количество (масса) его неизменна. А из этого прямо следует, что фактическим «источником», инициатором давления является именно объём газа, но никак не физическая структура его «молекул». Другими словами в данной формулировке априорно постулируется либо бесконечно малый объём «ядра» молекулы (нейтрона), в котором, собственно, и сосредоточена вся его масса. Либо постулируется бесконечно малая средняя плотность объёма нейтрона. Если принять, что нейтрон имеет шарообразную форму, то каждый элементарный объём этого шара имеет нулевую (бесконечно малую) плотность. Всё это прямо следует из утверждения, что давление зависит только от плотности газа. Но этот постулат автоматически допускает сжатие до бесконечности, то есть уже на этом этапе заложены, постулированы основы возникновения сингулярности. Другими словами, сделано утверждение: сингулярность неизбежна, теперь осталось только описать это с помощью уравнений. Ответ известен, нужно подогнать под него решение. Поэтому естественным следствием будет вывод: «Если тело, сжимаясь, сократилось до размеров, близких к гравитационному радиусу, то никакие силы не в состоянии остановить дальнейшее сжатие и тело будет неудержимо падать в себя – коллапсировать» [20]. По этой же причине все расчеты, естественно, приводят к результатам, в которых на этапе коллапса сила тяготения существенно превышает силы давления. А раз так, то в этом случае вполне допустимо пренебречь давлением, считать, что частицы на поверхности звезды свободно падают в ее поле тяготения. Считается, что сжатие вещества звезды имеет характер адиабатического процесса, то есть процесса без теплового обмена с внешней средой [1], в котором давление и плотность связаны соотношением вида рс ~ r^g_c (g называется показателем адиабаты). Поскольку плотность вещества определяется размерами звезды rc ~ 1/R³, делается вывод, что при показателе адиабаты g < 4/3 любое случайное малое гидродинамическое сжатие будет нарастать. В этом случае никакая упругость вещества не сможет предотвратить гравитационный коллапс [9]. В приведённом описании постулат о плотности явно не просматривается, но легко выводится при анализе. Поскольку плотность вещества определяется только размерами звезды, нет никаких пределов для их (размеров) уменьшения вплоть до нуля. Ограничением такому сжатию может препятствовать только прямо и отчетливо постулированное свойство конечной жесткости вещества. То есть, некоторого объёма вещества, при котором указанная адиабатическая связь нарушается. Физически это может означать сжатие вещества звезды до некоторого ядерного состояния, когда для дальнейшего сжатия нейтронов требуется силы, превышающие давление газа на много порядков. Это должно напоминать процесс сближения двух магнитов (одноименными полюсами). До некоторого момента магниты «мягко» сопротивляются сближению. Но после их соприкосновения уже недостаточно никакой механической силы для дальнейшего сближения. Поведение вырожденного ферми газа при образовании нейтронных звезд и начале гравитационного коллапса имеет достаточно качественное формальное описание. Хотя зачастую и отмечается, что в этом вопросе не всё выяснено до конца: «Целый комплекс процессов, сопровождающих термоядерные взрывы в ядрах и гравитационный коллапс, еще не до конца ясен и требует дальнейшего изучения» [41]. При гравитационном коллапсе звезда может образовать белый карлик. При ещё большей массе звезды давление её вышележащих слоев будет так велико, что электроны «вдавливаются» в протоны, образуя нейтроны. При этом и образуется нейтронный вырожденный ферми-газ, давление которого в определённой степени препятствует сжатию вещества звезды. «Давление нейтронного вырожденного газа препятствует дальнейшему сжатию звезды» [16]. Вырождение нейтронного газа происходит в процессе эволюции звезды, поглощения ею внешнего вещества. Плотность и температура в центре звезды при этом непрерывно возрастают, приводя к изменению состояния вещества звезды: «При росте плотности физическое состояние вещества может кардинально измениться из-за квантовомеханических эффектов (т.н. вырождение газа). Газ рассматривается как идеальный, пока взаимодействие между частицами пренебрежимо мало» [25]. Далее в цитируемой лекции отмечается, что давление газа, противодействующее сжатию, не зависит от температуры. Однако, важно не то, от чего зависит давление. Важно, что сущность процесса противодействия сжатию однозначно определено и исследуется поведение только этого процесса, то есть свойства сжатого вырожденного нейтронного ферми-газа. То, что он не способен противостоять гравитации, ни у кого не вызывает сомнений: «Гравитационному сжатию системы противостоит давление Ферми-газа. Если масса кора сверхновой больше удвоенной массы Солнца, гравитационные силы преодолевают давление Ферми-газа, и звезда превращается в черную дыру» [5]. Хотя величина массы звезды, ведущая к образованию черной дыры, установлена как предел Оппенгеймера — Волкова, вопрос о её величине и структуре звезд окончательно не решён: «Установить, насколько это значение близко к реальному пределу, чрезвычайно сложно: астрофизики пока не определились ни с составом нейтронной звезды, ни с тем, как именно следует описывать взаимодействие её компонентов» [35]. Таким образом, выходит, что неизбежность возникновения сингулярности опирается на достаточно условный фундамент. Одних только утверждений и выкладок о свойствах вырожденных ферми-газов, всё-таки недостаточно. Рассмотрим ещё один довод в пользу сингулярности. При достижении гравитационного предела, звезда становится «невидимой». Следовательно, поверхность звезды однозначно должна быть под горизонтом. Если перед началом коллапса звезда имела существенно больший размер, чем занимает шар с гравитационным радиусом, то сжатие вещества звезды неизбежно. И напротив, если радиус звезды до начала коллапса меньше гравитационного, то нет никаких веских оснований утверждать, что звезда вдруг уменьшила свой радиус. Видимо, в этом случае в момент коллапса радиус звезды и её гравитационный радиус тождественно равны. Процессы, происходящие сразу после коллапса Очевидно, что у сверхмассивной черной дыры разницу между сингулярностью и «атомным ядром» по внешним проявлениям «распознать» невозможно в принципе. Что сингулярность, что плотно сжатое нейтронное атомное ядро – всё это скрыто за горизонтом и что там находится на самом деле, не видно. Но для черных дыр начального, минимального размера разница может оказаться заметной. Как известно, согласно пределу Оппенгеймера-Волкова такой предельный размер черной дыры существует. Это такая максимальная масса нейтронной звезды, при которой давление вырожденного нейтронного газа ещё может компенсировать силы гравитации, не давая звезде коллапсировать в чёрную дыру. Следовательно, для черной дыры такая масса, наоборот, является минимальной: «Одновременно предел Оппенгеймера – Волкова является нижним пределом массы чёрных дыр, образующихся в ходе эволюции звёзд» [26]. По современным данным нижний предел массы черной дыры лежит в пределах 2,5—3 солнечных масс, а из известных черных дыр самая маломассивная имеет массу около 3,8 солнечной массы. Давайте рассмотрим такую черную дыру с предельно малой массой в 2,5 солнечных. Интересует, могут ли нейтроны с такой общей массой «поместиться» в пределах горизонта черной дыры. Если это невозможно, то, следовательно, у сингулярности есть веские основания. Если же общий объём нейтронов окажется меньше объёма сферы с гравитационным радиусом, то принципиальных оснований привлекать сингулярность не будет. Нейтронная звезда просто увеличила свой гравитационный радиус, радиус горизонта за пределы своей физической поверхности. Нет никакого смысла утверждать, что нейтронное вещество стало сжиматься к центру, «падать на сингулярность». Даже при дальнейшем неограниченном росте массы звезды нет веских оснований «давать» нейтронам такую способность уплотнения до бесконечности. Горизонт прячет от внешнего наблюдателя тело звезды и представления o сингулярности с бесконечно малым, даже нулевым радиусом выглядит как мистический домысел. Вычислим объём выбранной предельной нейтронной звезды на грани её коллапса, перехода в состояние черной дыры, исходя из следующих приблизительных данных: Масса покоя нейтрона, Mn 2x10^-27 кг Радиус нейтрона, rn 4x10^-16 м Гравитационная постоянная, G 6,67x10⁻¹¹ м³с⁻²кг⁻¹ Масса Солнца, Мс 1,99x10³⁰ кг Скорость света, с 299`792`458 м/с Итак, поскольку нейтронная звезда превратилась в черную дыру, её поверхность теперь находится под горизонтом. Гравитационный радиус в этом случае, по крайней мере, не меньше радиуса нейтронного шара. Посмотрим, как соотносятся объем образовавшейся черной дыры и объем всех нейтронов, образовавших её при коллапсе исходной нейтронной звезды. Массу такой черной дыры возьмем равной минимально возможной критической массе в 2,5Мс. Для расчетов берём именно минимальную черную дыру, поскольку очевидно, что внутри сверхмассивной черной дыры ядро, что называется, «с головой» поместится под горизонтом: Поскольку произошёл коллапс, понятно, что радиус шара вещества звезды должен стать меньше или равным её гравитационному радиусу, который равен: 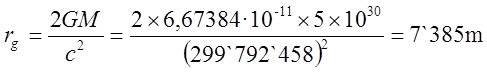Соответственно, объём V_ЧД под горизонтом возникшей при этом черной дыры равен: 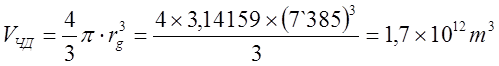Количество нейтронов, имеющих такую же суммарную массу, равно: 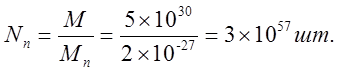Объём одного нейтрона без сжатия равен: 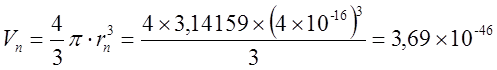Должен отметить, что сведений о радиусе нейтрона в свободном доступе немного. Поэтому используем те данные, которые удалось найти [6, 10, 17]. Таким образом, максимальный объём, который займут эти N_n нейтронов, составит: 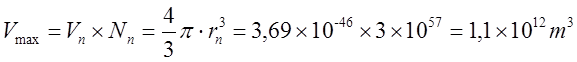Однако, этот объём не учитывает плотности упаковки сферических объектов. Известно, что при наиболее плотной упаковке шаров, они занимают в ней около 74% [34], следовательно, указанное число нейтронов займут несколько больший объем: 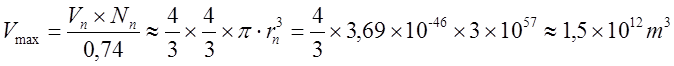Это весьма примечательный результат. Как видим, даже несжатые, свободно упакованные нейтроны, имеющие такую же массу, как и черная дыра, свободно помещаются под её горизонтом: 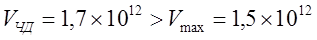Более того, это удивительный и совершенно неожиданный результат: такое невероятное совпадение объёмов – с точностью почти в 10 процентов! Пришлось несколько раз повторить расчеты, чтобы исключить вычислительные ошибки. Для радиусов нейтронной звезды и её гравитационного радиуса это совпадение ещё лучше – около 4 процентов! Такое, видимо, не случайное совпадение позволяет предположить, что предел Оппенгеймера-Волкова имеет вполне конкретное точное числовое значение. Для его определения используем полученные выше уравнения. В момент коллапса объём черной дыры равен: 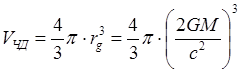Объём исходной нейтронной звезды в этот же момент равен: 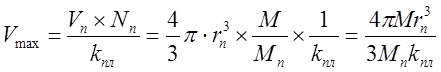В момент «ухода» поверхности нейтронной звезды под горизонт черной дыр объемы их, очевидно, равны. Совпадение объёмов и радиусов коллапсирующей нейтронной звезды и её гравитационного радиуса происходит при её массе, которую можно найти из этого равенства: 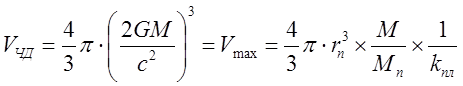После преобразований получаем: 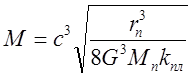Подставляем значения величин и вычисляем: 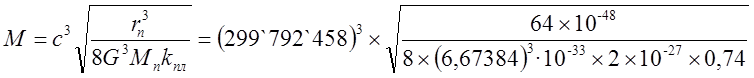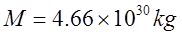Отношение массы черной дыры к массе Солнца: 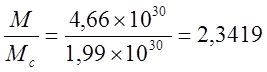Таким образом, предел Оппенгеймера-Волкова равен не диапазону, а конкретной величине - 2,34Мс. При такой величине массы нейтронной звезды происходит коллапс. В свою очередь, всё это означает, что представления о сингулярности, как и предполагалось, чрезмерны, плохо обоснованы. Нейтроны при коллапсе нейтронной звезды в черную дыру лишь ненамного плотнее «смыкают ряды». При этом не достигается даже плотность атомного ядра. Нужна ли в таком случае черной дыре сингулярность? Вычислим это соотношение для ядерной плотности. Как известно, сила гравитации на много порядков слабее сильного ядерного взаимодействия. Посмотрим, каковы будут силы, сжимающие звезду, силы, притягивающие нейтроны на её поверхности к центру звезды, когда радиус нейтронной звезды приблизится к её гравитационному радиусу. Мы определили, что масса черной дыры равна 5х10³⁰ кг. Нейтрон на поверхности звезды удалён от её центра на величину гравитационного радиуса, то есть, на r_g=7`385 метров. Следовательно, сила, с какой звезда гравитационно притягивает нейтрон на своей поверхности, равна: 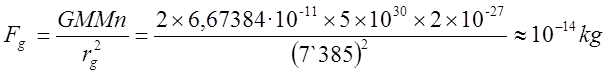Нейтрон лежит на поверхности и прижимается к ней, к следующему слою нейтронов. Два нейтрона находятся друг от друга на расстоянии не ближе, чем расстояние сильного взаимодействия между нуклонами в атомном ядре rсв~10^-15 м. Следовательно, сила их притяжения – условная «гравитационная сила сильного взаимодействия» F_гсв равна: 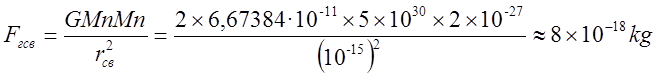Разумеется, это несколько условная сила гравитационного притяжения. Это сила, с которой нуклоны могли бы гравитационно притягиваться. Ядерные силы сильного взаимодействия сильнее гравитационной в 10³⁸ раз. То есть, нуклоны в ядре должны притягиваться с большей силой, чем гравитационное притяжение, силой ядерного сильного взаимодействия F_св: 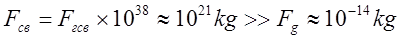Это та сила F_св, с которой нейтрон на поверхности звезды мог бы притягиваться к следующему слою, если бы входил в состав атомного ядра. Выходит, что силы гравитационного притяжения нейтронов звездой F_g на много порядков не хватает даже для того, чтобы они вступили в сильное ядерное взаимодействие, то есть, образовали бы в действительности огромное атомное ядро. «Перепрыгивание» в сингулярное падение, минуя состояния атомного ядра, выглядит как довольно-таки фантастический вариант. Но это «перепрыгивание», как утверждает гипотеза сингулярности, происходит чуть ли не одномоментно. Только что, до коллапса нейтроны на поверхности притягивались к центру звезды с относительно малой силой гравитации, и тут же, в одно мгновение притяжение возросло не просто в 10³⁸ раз, а многократно больше. Похоже на цирковой фокус, когда из пустой коробки вынимают кролика. Далее, как выше было показано в обзоре, сжатие до сингулярного состояния следует лишь из единственного, не очень убедительного постулата, что «жесткие» нейтроны с некоторым определённым радиусом превратились в пылинки с бесконечно малым объёмом и массой нейтрона, но с некоторой упругой сферической оболочкой, оказывающей давление при сжатии, - вырожденный фермионный газ. Представьте себе два обычных воздушных шара диаметром по 30 сантиметров, которые прижаты друг к другу с силой в 1 тонну, аналогом силы ядерного взаимодействия. Что в этом случае считать расстоянием между шарами? Разумеется, эти шары можно сжать до размеров горошины. Но изначально расстояние между их центрами при таком взаимодействии, очевидно, будет равно нулю. Куда и как приложить силу в одну тонну к этим шарам, чтобы разъединить их? Невозможно представить, чтобы такие эфемерные объекты могли притягиваться со столь непропорциональной силой. Нуклоны могут притягиваться с силой в 10³⁸ раз превосходящей силу гравитации. Для «газовой модели» расстояние между их центрами должно быть, как и в случае с шарами, близко к нулю. Но это явно противоречит экспериментам, поскольку атомные ядра разных веществ имеют разные и достаточно большие размеры. Выглядит довольно условной такая гипотеза о вырожденном фермионном газе, которая явно сводится к модели, в которой каждый элемент газа – молекула или пылинка – имеют массу, сосредоточенную «массивном ядре» нулевого объёма, и окружены упругой сферой, которая, собственно, и создаёт давление при сжатии. Сингулярность, возникающая на таком зыбком фундаменте, не должна рассматриваться как физическая реальность. Так как же быть в таком случае с предсказаниями сингулярности общей теорией относительности? Можно поступить просто. Во-первых, это предсказание – результат не очень хорошо обоснованной экстраполяции движения. Во-вторых, может быть, не следует требовать от геометрической теории – геометродинамики Эйнштейна, общей теории относительности, теории гравитации, которая рассматривает звёзды, галактики и даже их скопления как пыль, описания «химического» состава или свойств материала нейтронов и его поведения при сверхплотном сжатии? Если исходить из этих предположений, то можно прийти к выводу, что внутри черной дыры плотность вещества не является бесконечно большой, поскольку его объём не стремится к нулю. Напротив, давления плотно сжатого вещества, а это уже, очевидно, не вырожденный фермионный газ, вполне достаточно, чтобы удержать его от дальнейшего сжатия. То есть, можно использовать обычные физические законы для описания этого вещества. С другой стороны, отвергается главная «страшилка» теории относительности – обрыв геодезических, мировых линий. Проблема предсказания будущего и причинности внутри черной дыры связана лишь с недоступностью этой области для внешнего наблюдателя. Но в жизни мы по этому поводу не очень-то сокрушаемся. Если мы потеряли связи с нашими знакомыми, это не значит, что они уехали в Чернодырск (ироничное – от черной дыры – название города). Или горизонт Вселенной, принципиально недоступный для наблюдений? К тому же обнаружена гипотетическая возможность проникнуть под горизонт сверхмассивной черной дыры и затем вернуться во внешнюю область [30]. Но тогда как поступить с сингулярностью Большого Взрыва? Ведь общепризнанно и с этим согласился даже Ватикан, что наша Реальность, Бытие возникли в результате взрыва сингулярности. В начале этой статьи я привёл трактовку этого события как рождение Вселенной из «Ничто, Нигде и Никогда». И хотя многие космологи и физики по-прежнему вслух говорят о сингулярности, но тайком, негласно, каждый раз, тем не менее, протаскивают в свои теории нечто, существовавшее до сингулярности: то ли инфлатоны, то ли скалярные поля, то ли квантовые флуктуации чего-то квантового. И это не удивительно, логика-то противится: «Из ничего может возникнуть только ничто». Вместе с тем, более реалистичной выглядит возникновение Вселенной из классической вечной и бесконечной Материи в результате изменения её состояния, как торжество материалистической философии. В процессе, напоминающем, например, конденсацию перегретого пара, и который я условно называю веществолизацией материи, Материя приняла одну из бесчисленных своих форм – вещественную. Как произошел этот переход, сейчас не особо важно. Может быть, была всё-таки точка начала веществолизации-конденсации. Тогда по всему объёму Вселенной пробежала своеобразная волна, как при обычном взрыве. Может быть, Материя, обладающая бесчисленными неизвестными нам свойствами, перешла в новое состояние одномоментно, как это и выглядит при конденсации пара, замерзании переохлажденной воды или взрыве перегретой жидкости [27]. В конце этого, видимо, крайне быстрого процесса образовалась та самая ранняя сильно разогретая Вселенная. В дальнейшем все процессы можно рассматривать в рамках существующих представлений: образование частиц и всего остального. Граница Вселенной в этом случае ничем не ограничена и может простираться до бесконечности, как бесконечна сама Материя. Проблема изотропии также не возникает: состояние материи перед её веществолизацией полностью однородно, изотропно, поэтому нет никаких оснований вещественной форме иметь разные свойства на бесконечных удалениях друг от друга. Это же объясняет и плоскостность Вселенной: бесконечно протяженное пространство по определению – плоское, радиус кривизны равен бесконечности. Главное, что из теории изгоняется мистика сотворения. Иное объяснение получает и темная энергия. Поскольку процесс веществолизации может быть вечным, то в отдельных точках Вселенной равномерно в пространстве, появляются дополнительные «атомы пространства» - элементы вещественного физического вакуума [29]. Гравитационно связанные области не расширяются, потому что обилие вещества в них, видимо, препятствуют образованию новых «атомов пространства». Трудно пробиться через толпу. Также это объясняет и возможность сверхсветового разбегания галактик. Они не движутся под действием сил, они не движутся по инерции – таких скоростей не допускает теория относительности. Но расстояние между ними увеличивается – за счет появления новых «атомов пространства». Загадочная темная материя тоже может иметь под собой материальную основу. Неизвестные ныне формы проявления Материи могут обладать гравитационными свойствами. Впрочем, феномен тёмной материи сам по себе крайне противоречив и непоследователен [28]. (окончание)
Категория: Разное \| Добавил: m55 \| Теги: Сингулярность, нейтронная звезда, Анимация, черная дыра, Геодезическая, гравитационный радиус, Коллапс, Горизонт Событий, фермионный газ
Просмотров: 3073 \| Загрузок: 40