Путенихин П.В. Задача по квантовым вычислениям с решением
| [ Скачать с сервера (454.8 Kb) ] | 14.02.2016, 16:30 |
Путенихин П.В. m55@mail.ru Аннотация Рассмотрена в учебных целях задача по измерению поляризованных фотонных потоков с различной поляризацией с помощью одного и того же поляризатора. Вычисления вероятности прохождения этих фотонов произведены с использованием проективной математики квантовых вычислений. В большинстве учебников по квантовой информатике приводятся математические выражения для анализа квантовых схем. Для лучшего понимания механизмов квантовых вычислений рассмотрим в порядке практикума одну из частных задач по измерению состояния поляризованного потока фотонов. В общем случае поляризованный поток фотонов может быть описан волновой функцией следующего вида: 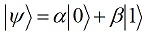 Каждый из фотонов рассматривается как кубит, описываемый этой волновой функцией. Коэффициенты α и β у всех кубитов одинаковые и в процессе решения задачи будут принимать некоторые определённые значения. Для изучения механизма измерения фотонов воспользуемся измерителем – поляризатором, наклоненным к горизонтали под углом 30о. Этот поляризатор может быть также описан волновой функцией, в нашем случае имеющей вид: 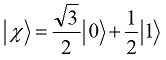 (1) Проектор такого измерителя, согласно математике квантовых вычислений, имеет вид: 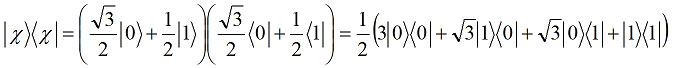 Графически исследуемый кубит (синяя стрелка) и поляризатор 30о (красная стрелка) можно изобразить таким образом: 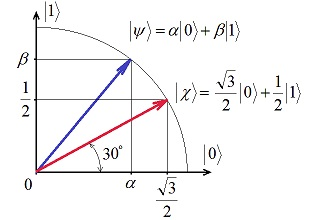 Исследуемый кубит на рисунке показан условно, для некоторых неопределённых заранее проекций α и β. На самом деле вектор кубита может иметь любой угол по отношению к поляризатору. Напротив, используемый поляризатор имеет фиксированный угол наклона 30о к горизонтали. Действие, которое поляризатор окажет на исследуемые произвольные кубиты, согласно математике квантовых вычислений описывается проектором: 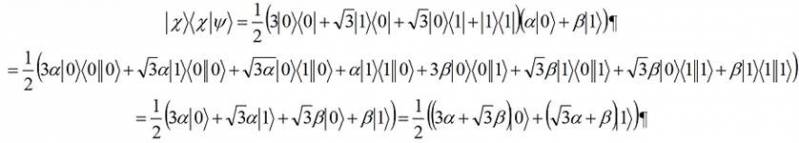 После преобразования полученного выражения можно увидеть, что после прохождения через поляризатор (проектор) исследуемый кубит |ψ> перейдёт в состояние поляризатора |χ>: 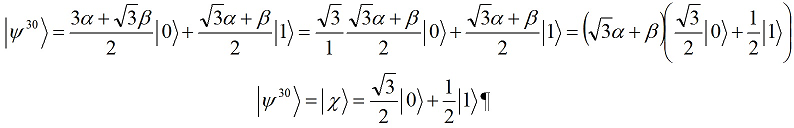 Итак, любой измеренный поляризатором фотон перешёл в состояние проектора. Но с какой вероятностью это произошло? Вероятность прохождения кубита через поляризатор найдём по формуле, предлагаемой математикой квантовых вычислений: 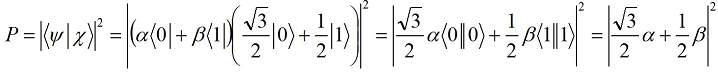 Исследуем теперь с помощью этого уравнения различные кубиты. Любой из этих кубитов после прохождения через поляризатор будет находиться в состоянии (1). Например, в простейшем случае, когда кубит коллинеарен поляризатору: 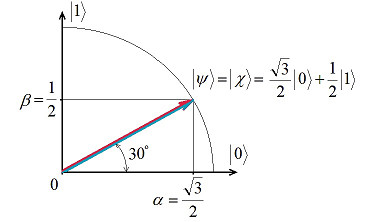 Вероятность прохождения через выбранный поляризатор такого коллинеарного кубита: 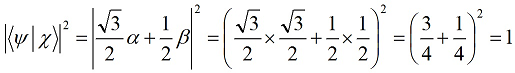 Действительно, если кубит и поляризатор параллельны (собственный проектор), то кубит будет переведён в его состояние достоверно, то есть через этот поляризатор пройдут все фотоны потока. Рассмотрим кубит, ортогональный нашему поляризатору: 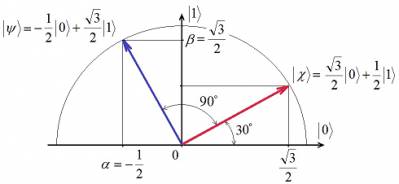 Вероятность прохождения через проектор такого ортогонального кубита: 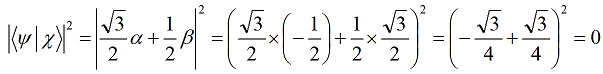 Так и должно быть: если поляризатор (проектор) имеет перпендикулярное направление к фотонам, то ни один фотон не пройдёт через него. Если угол между кубитом и поляризатором равен 30о: 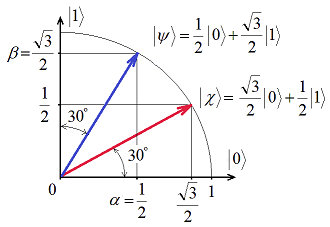 то вероятность прохождения кубита через этот поляризатор будет: 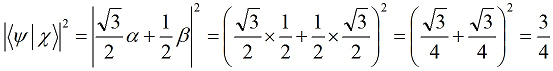 Прикидочно, «на глазок» это легко принять: кубит и проектор (поляризатор) почти параллельны, близки друг к другу, поэтому фотонов пройдёт достаточно много. Рассмотрим теперь кубит, имеющий поляризацию под углом 15о к нашему проектору: 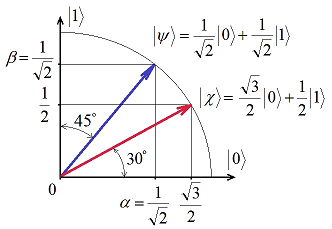 Вероятность прохождения через проектор такого наклонного кубита: 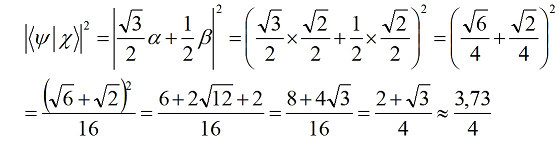 Здесь угол между поляризатором и кубитом ещё меньше, чем в предыдущем примере, поэтому пройдёт ещё больше фотонов, что также выглядит правдоподобно. Рассмотрим следующий кубит в состоянии |ψ>=|1>, то есть кубит, имеющий вертикальную поляризацию: 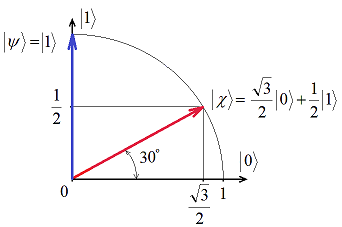 Этот кубит образует с поляризатором угол 60о и пройдёт через него с вероятностью: 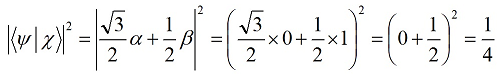 Угол между кубитом и поляризатором достаточно большой, поэтому вероятность прохождения кубитов через поляризатор невелика. Рассмотрим другой кубит с базисной поляризацией - в состоянии |ψ>=|0>, то есть, имеющий вертикальную поляризацию: 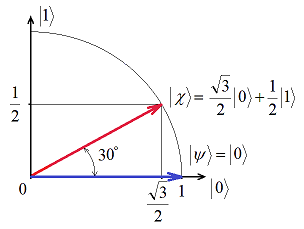 Вероятность его прохождения через поляризатор: 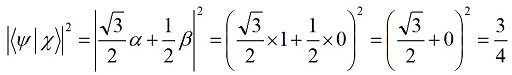 Здесь уже можно заметить совпадение. Такую же вероятность прохождения имеет и фотон, имеющий угол наклона 30о к вертикальной оси. И это совпадение не удивительно, ведь оба этих фотона образуют с поляризатором один и тот же угол - 30о. Ещё одно совпадение мы обнаружим при рассмотрении фотона, который образует с горизонтальной осью угол минус 30о: 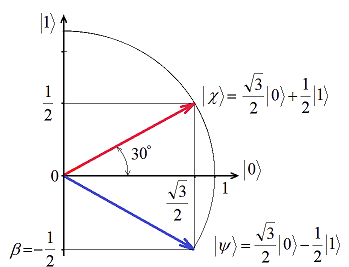 Этот фотон пройдёт через поляризатор с такой же вероятностью, что и вертикально поляризованный фотон: 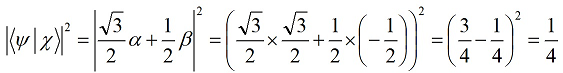 В этом совпадении тоже нет ничего не удивительно, ведь оба этих фотона образуют с поляризатором один и тот же угол - 60о. В заключение необходимо заметить, что полученные вероятности относятся к фотонам, прошедшим через поляризатор. А что произошло с фотонами, которые не прошли через него? Это легко выяснить экспериментально, если использовать расщепляющий поляризатор. В этом случае остальные фотоны все без исключения пройдут на его ортогональный выход. То есть, все фотоны, не прошедшие через наш поляризатор, имеют поляризацию, ортогональную к поляризации прошедшего фотона. Соответственно, вероятности их ортогонального прохождения равны разнице между полной вероятностью – единицей и вероятностью прохождения фотонов через наш поляризатор: 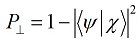 01.11.2013 Адрес полного текста статьи в интернете URL: http://samlib.ru/editors/p/putenihin_p_w/z01.shtml Иллюстрации и уравнения к статье (зеркала) http://samlib.ru/editors/p/putenihin_p_w/ https://cloud.mail.ru/public/8WpP/qeaUMAiGz https://yadi.sk/d/EZg36rrKmJDwk http://vixra.org/author/putenikhin_p_v | |
| Категория: Статьи | | | |
| Просмотров: 3371 | Загрузок: 87 | |
| Всего комментариев: 0 | |